1.2基本术语
特征向量:即示例,反映事件或对象在某方面的性质。例如,西瓜的色泽,敲声。
属性:例如 青绿 乌黑 清脆。
数据集:例如(色泽=青绿,根蒂=蜷缩,敲声=浊响),(色泽=浅白,根蒂=硬挺,敲声=清脆),(色泽=乌黑,根蒂=稍蜷,敲声=沉闷)……
例如,D = {X1,X2,……,Xm}表示包含m个示例的数据集。
Xi = (xi1;xi2;……;xid)每个示例有d个属性表述。
标记:预测结果信息,例如((色泽=青绿,根蒂=蜷缩,敲声=浊响),好瓜)。好瓜则为标记。
标记的集合,亦称:标记空间,输出空间。
样例:拥有标记信息的示例。用(xi,yi)表示样例。
分类:预测是离散值。例如:好瓜,坏瓜。
回归:预测的是连续值。例如:西瓜的成熟度0.89,0.37。输出空间y=R(实数集)
二分类:分正类,反类。样本空间--->输出空间 输出空间 = {+1,-1} 或{0,1}
多分类:|输出空间y|>2
聚类:分成若干组
监督学习:回归,分类。
无监督学习:聚类。
独立同分布:样本服从一个未知的分布,获得的每个样本呢都是独立的从这个分布上采样获得的。
1.3假设空间
归纳学习:广义--->从样例中学习
狭义:从训练数据中学得概念。
概念学习:(色泽=?)^(根蒂=?)^(敲声=?)
假设空间:若色泽,根蒂,敲声,各有3种可能取值。
假设空间大小规模:4*4*4+1=65;3+1=4 的两个加1都是是通配符的情况。
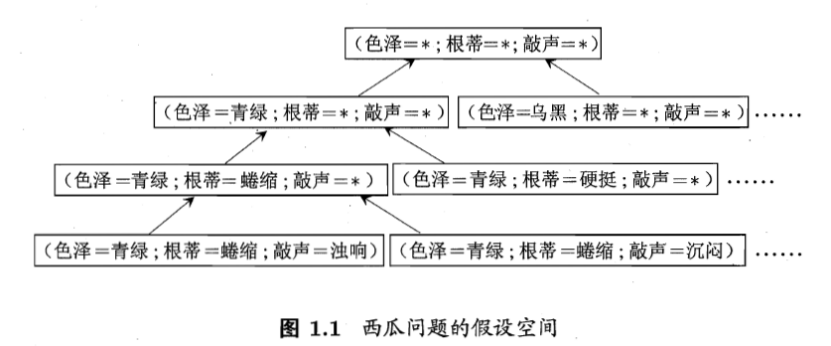
对假设空间自顶向下搜索,即训练。
版本空间:多个假设与训练集一致,即存在着一个与训练集一致的假设集合。

1.4归纳偏好
我的理解:当在现有的模型中,出现新的样本,既可以归为正类,也可以归为反类。我们设定一个优先级,根据这个偏好去归纳。
奥卡姆剃刀:若有多个假设与观察一致,选最简单的那个。例如曲线A的描述方程要比B简单的多。自然偏好A。

此时剃刀不适用。

假设样本空间和假设空间都是离散的.令代表算法基于训练数据X产生假设h的概率,再令f代表我们学习的真实目标函数。的”训练集外误差”,即在训练集外的所有样本上的误差为
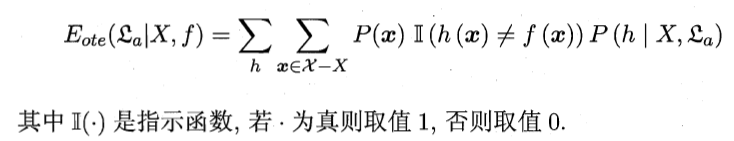

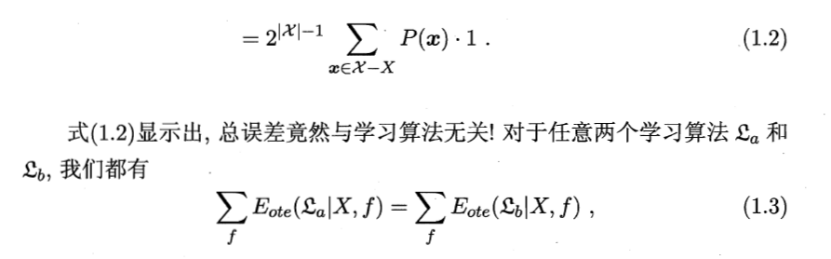
上面式中所有可能性之和自然是为1。
在问题出现的机会相同,所有问题同等重要,对于任意两个学习算法,其总误差相等,期望性能相同。
脱离具体问题谈算法的好坏无意义。




