数据结构学习笔记07散列查找(哈希表)

1.散列表(Hash)

查找的本质: 已知对象找位置。
　　有序安排对象：全序、半序
　　直接“算出”对象位置：散列
　　时间复杂度几乎是常量：O（1），即查找时间与问题规模无关

散列查找法的两项基本工作：
　　计算位置：构造散列函数确定关键词存储位置；
　　解决冲突：应用某种策略解决多个关键词位置相同的问题

散列（Hashing） 的基本思想是：
　　①以关键字key为自变量，通过一个确定的函数 h（散列函数），计算出对应的函数值h(key)，作为数据对象的存储地址。
　　②可能不同的关键字会映射到同一个散列地址上，即h(keyi) = h(keyj)（当keyi ≠keyj），称为“冲突(Collision)”。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　----需要某种冲突解决策略

2.散列函数的构造方法

散列函数两个关键：

　　①计算简单，以便提高转换速度；
　　②关键词对应的地址空间分布均匀，以尽量减少冲突。

 

数字关键词的散列函数构造

①直接定址法
　　取关键词的某个线性函数值为散列地址，即
　　h(key) = a * key + b (a、b为常数)

②除留余数法
　　散列函数为：h(key) = key mod p　　(一般p取素数)

 

③数字分析法
　　分析数字关键字在各位上的变化情况，取比较随机的位作为散列地址
　　　　Eg：取11位手机号码key的后4位作为地址：
　　　　散列函数为：h(key) = atoi(key+7)  (char *key)

④折叠法
　　把关键词分割成位数相同的几个部分，然后叠加

　　　　Eg： 56793542
　　　　　　　  542
　　　　　　　  793
　　　　　　  + 056
　　　　　　　———
　　　　　　　 1391
　　　　　　　　　　　　h(56793542) = 391

 

⑤平方取中法
　　　　Eg： 56793542
　　　　　　56793542
　　　　　x 56793542
　　　　—————————
　3225506412905764
　　　　　　　　　　　　h(56793542) = 641

 

字符关键词的散列函数构造

①一个简单的散列函数——ASCII码加和法
　　对字符型关键词key定义散列函数如下：
　　h(key) = (Σkey[i]) mod TableSize

②简单的改进——前3个字符移位法(易造成空间浪费)
　　h(key)=(key[0]*27^2 + key[1]*27 + key[2]) mod TableSize

③好的散列函数——移位法
　　涉及关键词所有n个字符，并且分布得很好：

　　Eg：h(“abcde”)=‘a’*324+’b’*323+’c’*322+’d’*32+’e’

　　Index Hash ( const char *Key, int TableSize )
　　{
　　　　unsigned int h = 0; /* 散列函数值，初始化为0 */
　　　　while ( *Key != ‘\0’) /* 位移映射 */
　　　　　　h = ( h << 5 ) + *Key++;
　　　　return h % TableSize;
　　}

 

3.冲突处理方法 及 性能分析

平均查找长度（ASL）用来度量散列表查找效率：成功、不成功
　　关键词的比较次数，取决于产生冲突的多少
　　影响产生冲突多少有以下三个因素：
　　　　①散列函数是否均匀；
　　　　②处理冲突的方法；
　　　　③散列表的装填因子α。

 

开放地址法：换个位置　　一旦产生了冲突（该地址已有其它元素），就按某 种规则去寻找另一空地址

①线性探测法(Linear Probing)
　　线性探测法：以增量序列 1，2，……，（TableSize -1）循环试探下一个存储地址。

 

　　成功平均查找长度(ASLs) 查找表中关键词的平均查找比较次数
　　不成功平均查找长度 (ASLu) 不在散列表中的关键词的平均查找次数

 

②平方探测法 (Quadratic Probing)--- 二次探测

　　平方探测法：以增量序列1^2，-1^2，2^2，-2^2，……，q^2，-q^2且q ≤ [TableSize/2](向下取整) 循环试探下一个存储地址。

　　Eg：平方探测法如何找到未填充空间

      

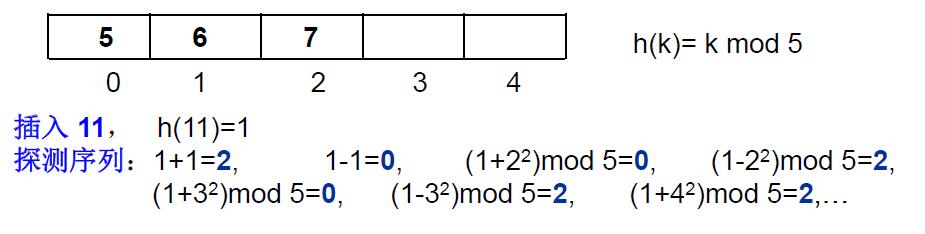
　　定理：如果散列表长度TableSize是某个4k+3（k是正整数）形式的素数时，平方探测法就可以探查到整个散列表空间。

③双散列探测法 (Double Hashing)

双散列探测法: di 为i*h2(key)，h2(key)是另一个散列函数探测序列成：h2(key)，2h2(key)，3h2(key)，……(对任意的key，h2(key) ≠ 0 )

　　探测序列还应该保证所有的散列存储单元都应该能够被探测到。选择以下形式有良好的效果：
　　　　h2(key) = p - (key mod p) (p < TableSize，p、TableSize都是素数)

④再散列 (Rehashing)

当散列表元素太多（即装填因子 α太大）时，查找效率会下降；

　　实用最大装填因子一般取 0.5 <= α<= 0.85

当装填因子过大时，解决的方法是加倍扩大散列表，这个过程叫做“再散列（Rehashing）”

链地址法:同一位置的冲突对象组织在一起

　　分离链接法：将相应位置上冲突的所有关键词存储在同一个单链表中

　　

 

　　Eg: h(key) = key mod 11

 

 

 

 

 

所有地址链表的平均长度定义成装填因子α，α有可能超过1。
不难证明：其期望探测次数 p为：

 

4.性能分析

　　①选择合适的 h(key) ，散列法的查找效率期望是常数O(1)，它几乎与关键字的空间的大小n无关！也适合于关键字直接比较计算量大的问题
　　②它是以较小的α为前提。因此，散列方法是一个以空间换时间
　　③散列方法的存储对关键字是随机的，不便于顺序查找关键字，也不适合于范围查找，或最大值最小值查找。

开放地址法

　　优：散列表是一个数组，存储效率高，随机查找。
　　缺：散列表有“聚集”现象

分离链法

　　散列表是顺序存储和链式存储的结合，链表部分的存储效率和查找效率都比较低。

 

　　优：关键字删除不需要“懒惰删除”法，从而没有存储“垃圾”。

　　缺：太小的α可能导致空间浪费，大的α又将付出更多的时间代价。不均匀的链表长度导致时间效率的严重下降。

 

5.

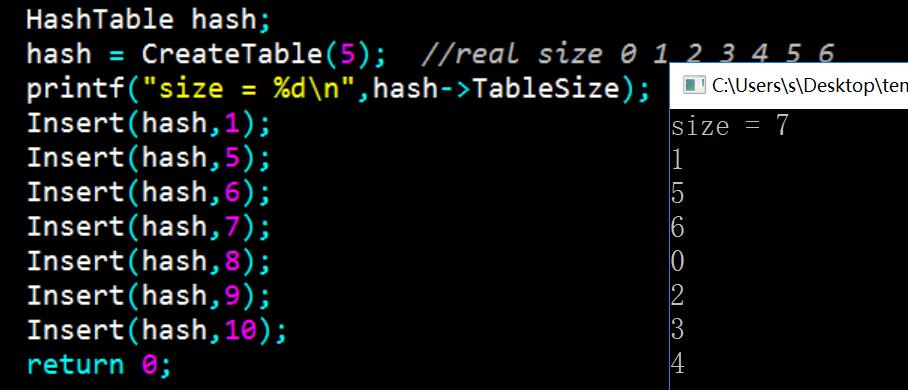
//哈希表平方探测法
#include <stdio.h> 
#include <stdlib.h>
#include <math.h>

#define MAXTABLESIZE 100000 /* 允许开辟的最大散列表长度 */
typedef int ElementType;    /* 关键词类型用整型 */
typedef int Index;          /* 散列地址类型 */
typedef Index Position;     /* 数据所在位置与散列地址是同一类型 */
/* 散列单元状态类型，分别对应：有合法元素、空单元、有已删除元素 */
typedef enum { Legitimate, Empty, Deleted } EntryType;
 
typedef struct HashEntry Cell; /* 散列表单元类型 */
struct HashEntry{
    ElementType Data; /* 存放元素 */
    EntryType Info;   /* 单元状态 */
};
 
typedef struct TblNode *HashTable; /* 散列表类型 */
struct TblNode {   /* 散列表结点定义 */
    int TableSize; /* 表的最大长度 */
    Cell *Cells;   /* 存放散列单元数据的数组 */
};

/* 返回大于N且不超过MAXTABLESIZE的最小素数 */
int NextPrime( int N )
{ 
    int i, p = (N%2)? N+2 : N+1; /*从大于N的下一个奇数开始 */
 
    while( p <= MAXTABLESIZE ) {
        for( i=(int)sqrt(p); i>2; i-- )
            if ( !(p%i) ) break; /* p不是素数 */
        if ( i==2 ) break; /* for正常结束，说明p是素数 */
        else  p += 2; /* 否则试探下一个奇数 */
    }
    return p;
}
 
HashTable CreateTable( int TableSize )
{
    HashTable H;
    int i;
 
    H = (HashTable)malloc(sizeof(struct TblNode));
    H->TableSize = NextPrime(TableSize);/* 保证散列表最大长度是素数 */
    H->Cells = (Cell *)malloc(H->TableSize*sizeof(Cell));/* 声明单元数组 */
    /* 初始化单元状态为 空单元 */
    for( i=0; i<H->TableSize; i++ )
        H->Cells[i].Info = Empty;
 
    return H;
}

Position Hash(ElementType Key, int TableSize )
{
    return Key % TableSize;
}

/*平方探测法1^2，-1^2，2^2，-2^2 …*/ 
Position Find( HashTable H, ElementType Key )
{
    Position CurrentPos, NewPos;
    int CNum = 0; /* 记录冲突次数 */
 
    NewPos = CurrentPos = Hash( Key, H->TableSize ); /* 初始散列位置 */
    /* 当该位置的单元非空，并且不是要找的元素时，发生冲突 */
    while( H->Cells[NewPos].Info!=Empty && H->Cells[NewPos].Data!=Key ) {
                                           /* 字符串类型的关键词需要 strcmp 函数!! */
        /* 统计1次冲突，并判断奇偶次 */
        if( ++CNum%2 ){ /* 奇数次冲突 */
            NewPos = CurrentPos + (CNum+1)*(CNum+1)/4; /* 增量为+[(CNum+1)/2]^2 */
            if ( NewPos >= H->TableSize )
                NewPos = NewPos % H->TableSize; /* 调整为合法地址 */
        }
        else { /* 偶数次冲突 */
            NewPos = CurrentPos - CNum*CNum/4; /* 增量为-(CNum/2)^2 */
            while( NewPos < 0 )
                NewPos += H->TableSize; /* 调整为合法地址 */
        }
    }
    return NewPos; /* 此时NewPos或者是Key的位置，或者是一个空单元的位置（表示找不到）*/
}

bool Insert( HashTable H, ElementType Key )
{
    Position Pos = Find( H, Key ); /* 先检查Key是否已经存在 */
    if( H->Cells[Pos].Info != Legitimate ) { /* 如果这个单元没有被占，说明Key可以插入在此 */
        H->Cells[Pos].Info = Legitimate;
        H->Cells[Pos].Data = Key;
        /*字符串类型的关键词需要 strcpy 函数!! */
        return true;
    }
    else {
        printf("键值已存在");
        return false;
    }
}

int main()
{
    HashTable hash;
    hash = CreateTable(5);    //real size 0 1 2 3 4 5 6
    printf("size = %d\n",hash->TableSize);
    Insert(hash,1);
    Insert(hash,5);
    Insert(hash,6);
    Insert(hash,7);
    Insert(hash,8);
    Insert(hash,9);
    Insert(hash,10);
    return 0;
}

 

//分离链接法
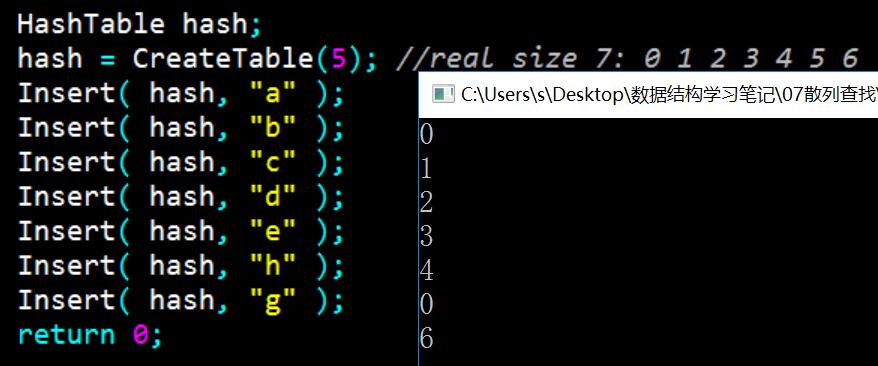
#include <iostream>
#include <cstdio> 
#include <cstdlib>
#include <cstring>
#include <math.h>
using namespace std;

#define MAXTABLESIZE 100000 /* 允许开辟的最大散列表长度 */
#define KEYLENGTH 15                   /* 关键词字符串的最大长度 */
typedef char ElementType[KEYLENGTH+1]; /* 关键词类型用字符串 */
typedef int Index;                     /* 散列地址类型 */
 
/******** 以下是单链表的定义 ********/
typedef struct LNode *PtrToLNode;
struct LNode {
    ElementType Data;
    PtrToLNode Next;
};
typedef PtrToLNode Position;
typedef PtrToLNode List;
/******** 以上是单链表的定义 ********/
 
typedef struct TblNode *HashTable; /* 散列表类型 */
struct TblNode {   /* 散列表结点定义 */
    int TableSize; /* 表的最大长度 */
    List Heads;    /* 指向链表头结点的数组 */
};
 
int NextPrime( int N )
{ /* 返回大于N且不超过MAXTABLESIZE的最小素数 */
    int i, p = (N%2)? N+2 : N+1; /*从大于N的下一个奇数开始 */
 
    while( p <= MAXTABLESIZE ) {
        for( i=(int)sqrt(p); i>2; i-- )
            if ( !(p%i) ) break; /* p不是素数 */
        if ( i==2 ) break; /* for正常结束，说明p是素数 */
        else  p += 2; /* 否则试探下一个奇数 */
    }
    return p;
}

HashTable CreateTable( int TableSize )
{
    HashTable H;
    int i;
 
    H = (HashTable)malloc(sizeof(struct TblNode));
    H->TableSize = NextPrime(TableSize);/* 保证散列表最大长度是素数 */
    H->Heads = (List)malloc(H->TableSize*sizeof(struct LNode));/* 以下分配链表头结点数组 */
    
    /* 初始化表头结点 */
    for( i=0; i<H->TableSize; i++ ) {
         H->Heads[i].Data[0] = '\0';
         H->Heads[i].Next = NULL;
    }
 
    return H;
}

Index Hash(ElementType Key, int TableSize )
{
    
    return (*Key - 'a') % TableSize;
}


Position Find( HashTable H, ElementType Key )
{
    Position P;
    Index Pos;
     
    Pos = Hash( Key, H->TableSize ); /* 初始散列位置 */
    P = H->Heads[Pos].Next; /* 从该链表的第1个结点开始 */
    /* 当未到表尾，并且Key未找到时 */ 
    while( P && strcmp(P->Data, Key) )
        P = P->Next;
 
    return P; /* 此时P或者指向找到的结点，或者为NULL */
}

bool Insert( HashTable H, ElementType Key )
{
    Position P, NewCell;
    Index Pos;
     
    P = Find( H, Key );
    if ( !P ) { /* 关键词未找到，可以插入 */
        NewCell = (Position)malloc(sizeof(struct LNode));
        strcpy(NewCell->Data, Key);
        Pos = Hash( Key, H->TableSize ); /* 初始散列位置 */ 
        /* 将NewCell插入为H->Heads[Pos]链表的第1个结点 */
        NewCell->Next = H->Heads[Pos].Next;
        H->Heads[Pos].Next = NewCell; 
        return true;
    }
    else { /* 关键词已存在 */
        printf("键值已存在");
        return false;
    }
}

void DestroyTable( HashTable H )
{
    int i;
    Position P, Tmp;
     
    /* 释放每个链表的结点 */
    for( i=0; i<H->TableSize; i++ ) {
        P = H->Heads[i].Next;
        while( P ) {
            Tmp = P->Next;
            free( P );
            P = Tmp;
        }
    }
    free( H->Heads ); /* 释放头结点数组 */
    free( H );        /* 释放散列表结点 */
}

int main()
{
    HashTable hash;
    hash = CreateTable(5); //real size 7: 0 1 2 3 4 5 6
    Insert( hash, "a" );
    Insert( hash, "b" );
    Insert( hash, "c" );
    Insert( hash, "d" );
    Insert( hash, "e" );
    Insert( hash, "h" );
    Insert( hash, "g" );
    return 0;
}