筛法素数打表方法
埃拉托斯特尼筛法,是一种公元前250年由古希腊数学家埃拉托斯特尼所提出的一种简单检定素数的算法。
给出要筛数值的范围n,找出以内的素数。先用2去筛,即把2留下,把2的倍数剔除掉;再用下一个质数,也就是3筛,把3留下,把3的倍数剔除掉;接下去用下一个质数5筛,把5留下,把5的倍数剔除掉;不断重复下去......。
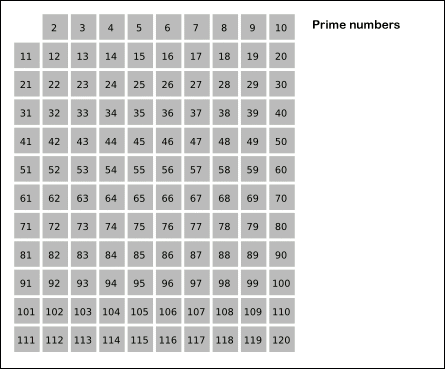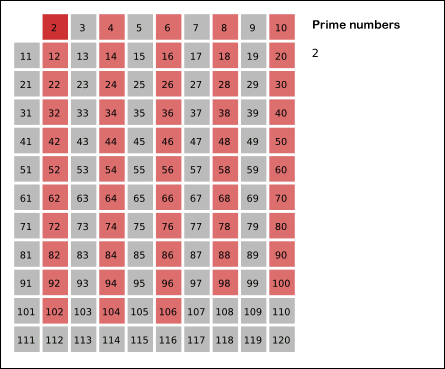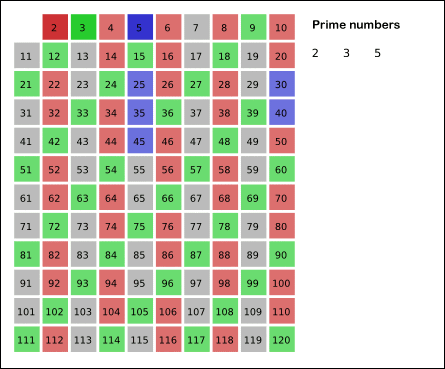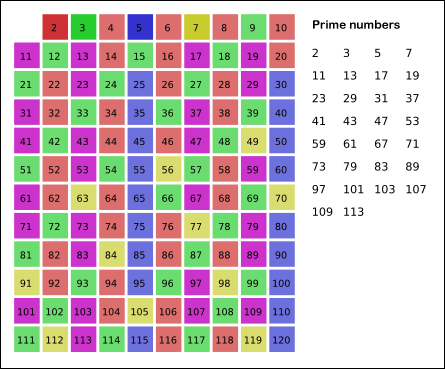
筛法素数时间复杂度o(log log n),基本接近线性,测试一亿个数据2.48秒
下面是比较优化的C++语言代码
const int maxn = 102410240;
bool isp[maxn];
void init()
{
memset(isp, true, sizeof(isp));
isp[0] = isp[1] = false;
const int max1 = sqrt(maxn + 0.5);
for(int i = 2; i <= max1; i++)
if(isp[i])
for(int j = i * i; j < maxn; j += i)
isp[j] = false;
}
下面是更好的,速度更快的线性筛法测试十亿个数据1.23秒:
const int maxn = 102410240;
bool check[maxn] = {1, 1};
int pri[maxn], tot;
void init()
{
for (int i = 2; i < maxn; ++i){
if (!check[i]) pri[tot++] = i;
for (int j = 0; j < tot && pri[j] * i < maxn; ++j){
check[pri[j]*i] = true;
if (!(i % pri[j])) break;
}
}
}

 浙公网安备 33010602011771号
浙公网安备 33010602011771号