AM信号的调制与解调

实验一 AM信号的调制与解调

1. 实验名称

AM信号的调制与解调实验

2. 实验目的

1. 了解AM信号的产生原理与实现方法

2. 了解调幅波调制系数的意义和方法

3. 了解AM信号解调原理与实现方法

3. 实验原理

幅度调制是用调制信号去控制高频载波的振幅，使之随调制信号作线性变化的过程。调幅信号的包络与调制信号成正比。

3.1 调制方法一

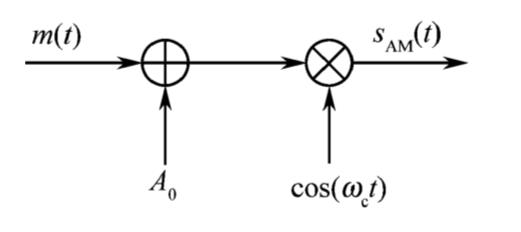
调制方法一采用基带信号叠加直流信号再乘载波进行频谱搬移。

$$S_{AM}(t)=[A_0+m(t)]cos(w_{c}t)$$

$A_0$ 为外加直流分量；$m(t)$ 的均值为0。

• 模型

• 频谱

若m(t)为确知信号，则AM信号的频谱为

$$S_{AM}(w)=\pi A_0[\delta (w+w_c)+\delta (w-w_C))]+\frac{1}{2}[M(w+w_c)+M(w-w_c)]$$

• 带宽

AM信号是带有载波分量的双边带信号，其带宽是基带信号带宽$f_H$的2倍，即

$$B_{AM}=2f_H$$

• 功率

$$\begin{gathered} P_{AM}=\overline{s_{AM}^2(t)}=\overline{[A_0+m(t){]}^{2}co{s}^2(w_{c}t)} \\ =\overline{A_0^{2}co{s}^2(w_{c}t)}+\overline{m(t{)}^{2}co{s}^2(w_{c}t)}+\overline{2A_{0}m(t)co{s}^2(w_{c}t)} \\ =\frac{A_0^2}{2}+\frac{\overline{m^2(t)}}{2}=P_c+P_s \end{gathered}$$

其中，载波功率为$P_c=\frac{A_0^2}{2}$ , 边带功率为 $P_s=\frac{\overline{m^2(t)}}{2}$

因此，调制效率可以定义为：

$${\eta }_{AM}=\frac{P_s}{P_{AM}}=\frac{\overline{m^2(t)}}{A_0^2+\overline{m^2(t)}}$$

3.2 调制方法二

调制方法二采用DSB-SC信号叠加一个大载波形成。叠加载波的效果与方法一直流信号进行频谱搬移相仿。

$$\begin{gathered} S_{AM}(t)=S_{DSB-SC(t)}+A_{c}cos(2\pi f_{c}t) \\ =m(t)\cdot A^{\prime }cos(2\pi f_{c}t)+A_{c}cos(2\pi f_{c}t) \\ =A_c[1+a\cdot m_n(t)]cos(2\pi f_{c}t) \end{gathered}$$

定义调幅系数 $ a = \frac{A’|m(t){max}|}{A{c}}$

3.3 解调方法一

包络检波法

由波形可知，为了在解调时使用包络检波而不失真地恢复出原基带信号m(t)，要求，使AM信号的包络$ A_{0}+m(t)$总是正的；否则会出现“过调幅”现象，用包络检波解调时会发生失真。

3. 4 解调方法二

相干解调

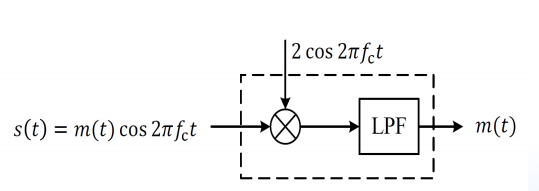
已调信号的恢复可以通过乘以载波，即将$m(t)$被搬移至基带，经过低通滤波器得到。   
 

4. 实验过程及内容

4.1 实验步骤

1. 依据理论在SystemView 中搭建仿真电路。

2. 调整电路参数，对比验证AM调制解调信号正确性。

3. 通过实验，理解实验原理，撰写实验报告。

4.2 参数设置

1. 参数设置总览

2. 变动参数设置截图

• 增益为1
• 增益为0.5
• 增益为2

5. 实验结果

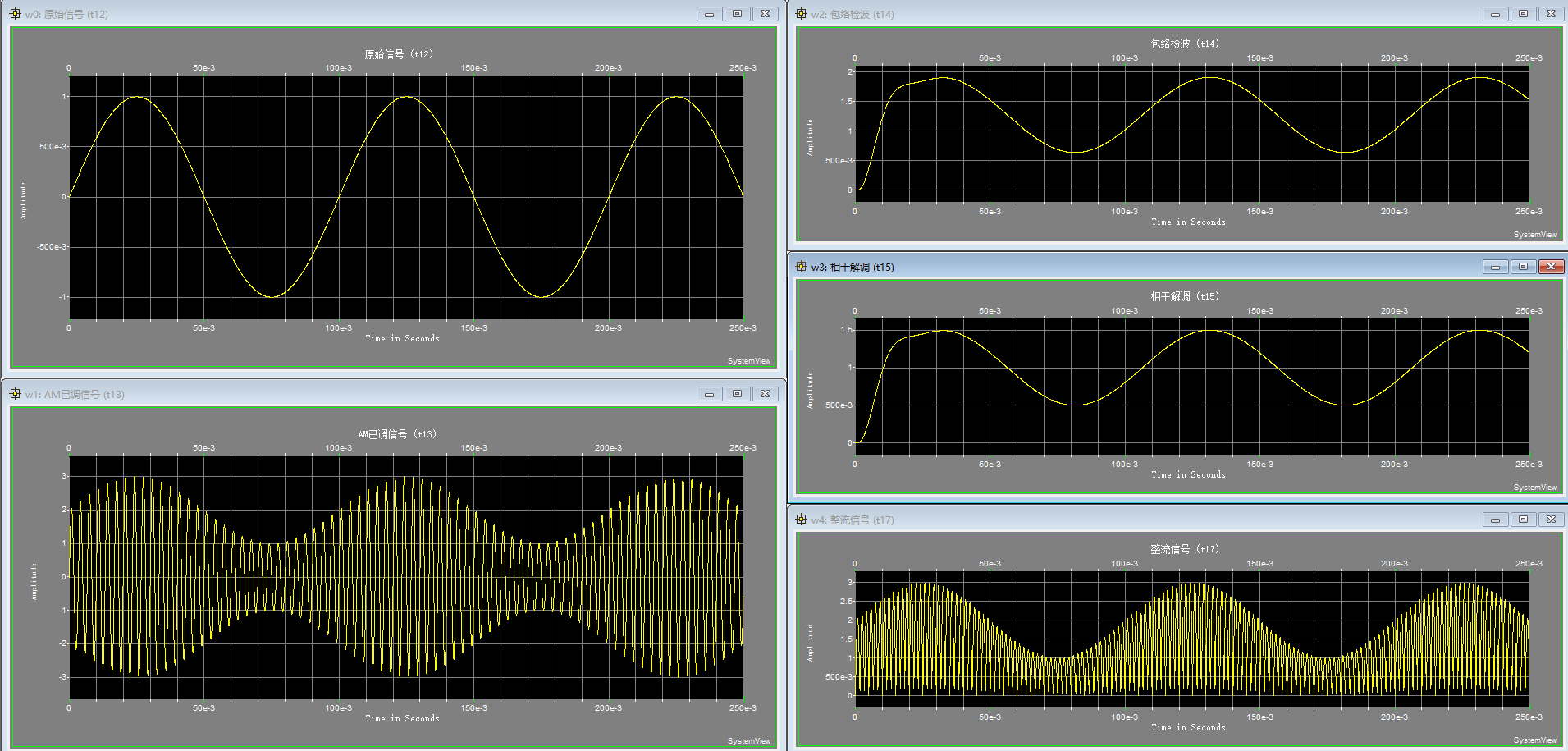
• 增益为2

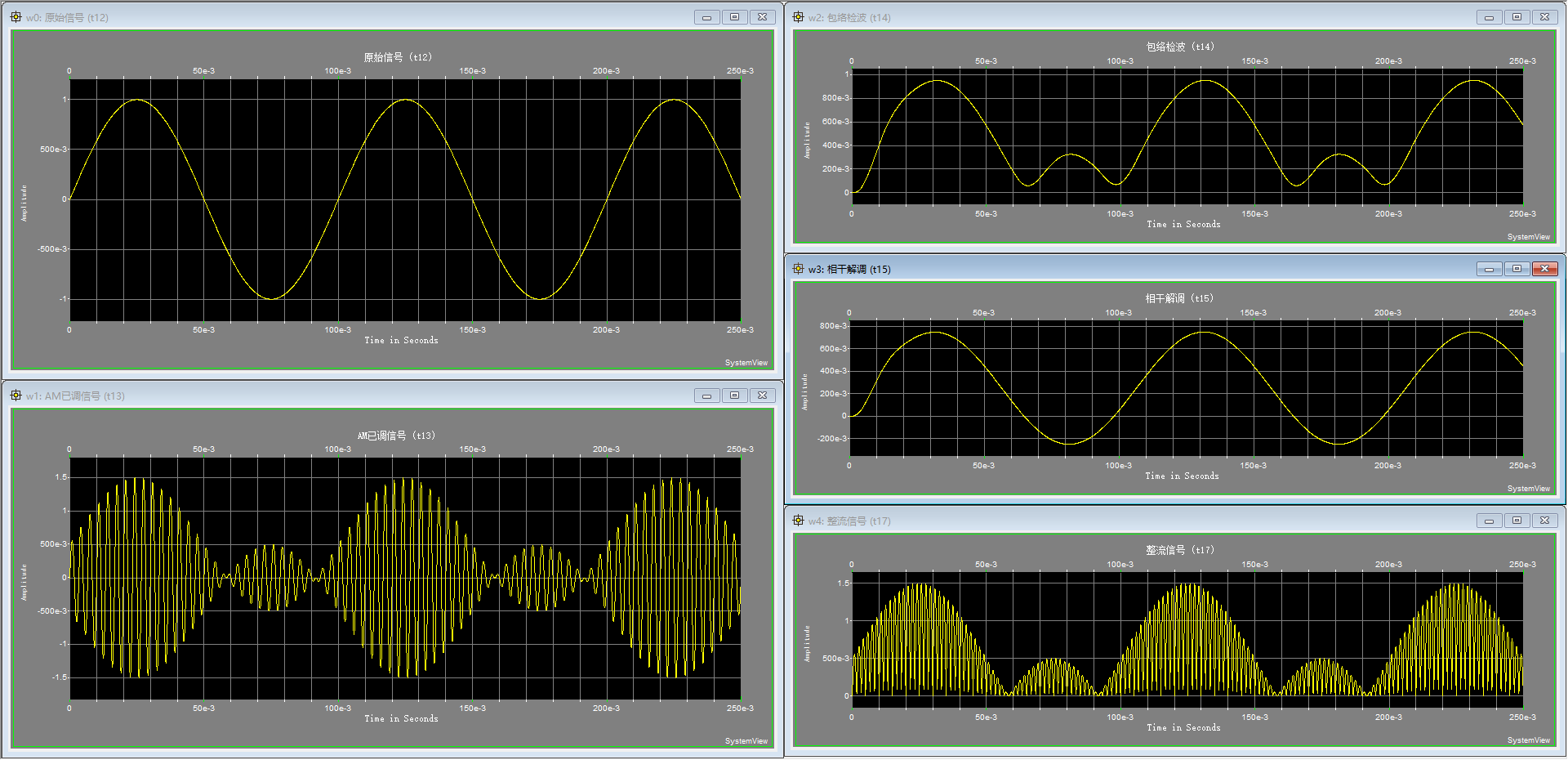
• 增益为0.5

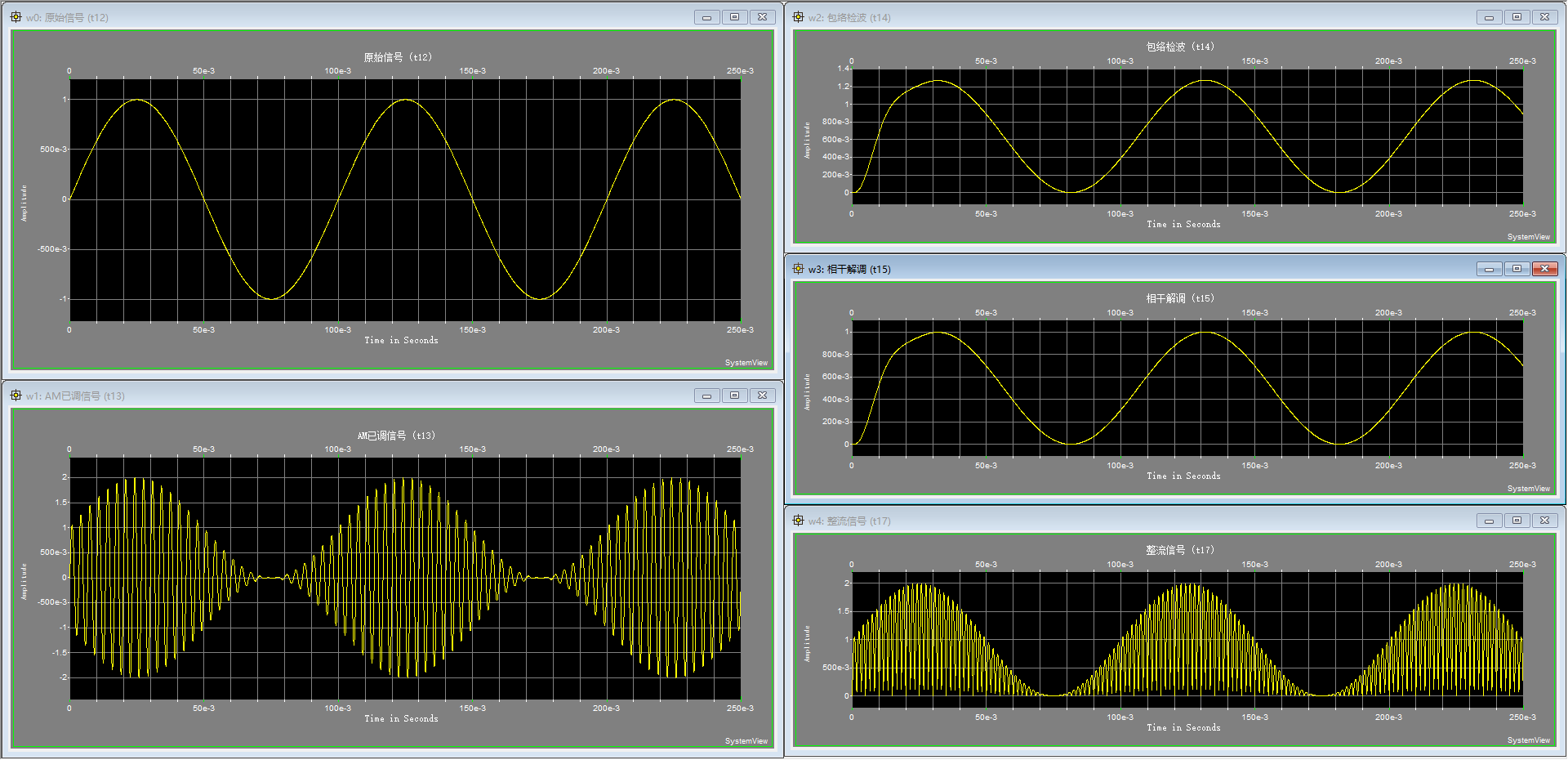
• 增益为1

6. 实验分析

本实验使用的是第二种（DSB-SC信号叠加一个大载波）的调制方法进行调制。并且试用两种解调方法（包络检波，相干解调）试图进行解调。

6.1 调制分析

根据实验结果，AM调制信号在不同增益之下有了不同的波形。请注意，这里的增益不是调制系数，而是电路中放大器的增益值。

• 增益为1

当电路中给载波的增益为1时，波形一个周期只有一个波峰。其实将其等效到第一种调制方法更容易直观理解。

不妨将附加的大载波等效为第一种调制方法的直流信号。

当载波增益为1的时候，相当于给正弦波一个+1V的直流，载波增益是多少，那么相当于直流就加多少。（这里默认载波幅度为1）

那么这个实验结果就很容易理解了。

上图包络用红色线条大致描绘，是$1+cos(wt)$的图像。经过载波调制之后得到了整幅黄色线条图像。

• 增益不为1

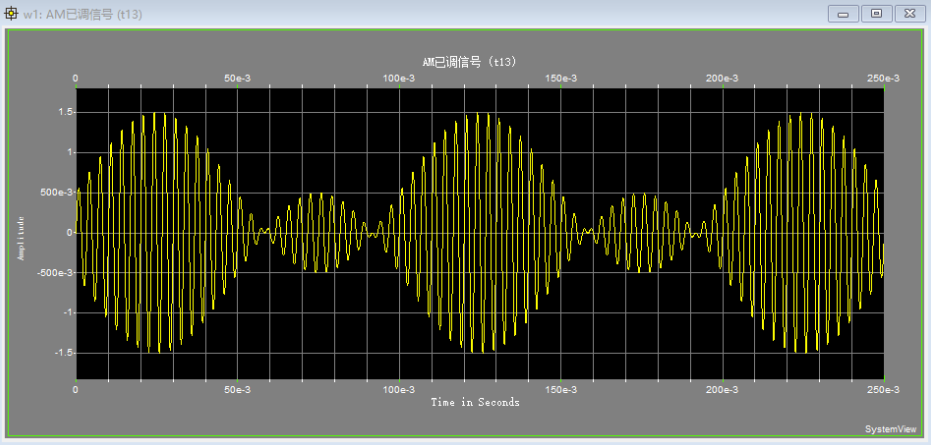
上图包络一个周期出现了两个峰值。同样的，可以等效至第一种调制方法去理解。

因为增益较小，相当于调“直流”没有加得足够使$m(t)$完全处于x轴线上方。增益为0.5， 相当于$m(t)$整体抬高0.5。

图中的最大值1.5 = 1 + 0.5， 最小值 0.5 = 1 - 0.5。

当增益为 2 的时候也是同样的道理，这里不赘述了。

6.2 解调分析

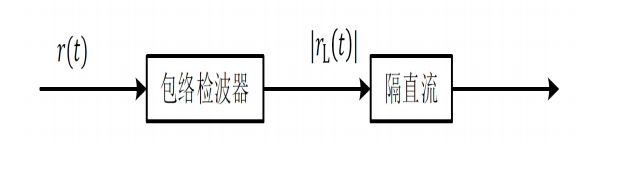
1. 包络检波

首先分析较为简单的包络检波，在电路中使用了整流器。

效果是将已调信号x轴线下的部分翻折至上部。

对于增益等于一和增益大于一的情况来说，沿用上文调制分析的思路，整流后的包络和等效调制方法一“抬升”之后的$m(t)$是一致的。

换一种说法，也就是在调制之前的m(t)的波形加上一个直流也就是等同于现在得到的包络。这样，只需要再进行割除直流就可以得到零均值的$m(t)$。

对于增益小于一的情况，整流后的包络等效调制方法一“抬升”之后的$m(t)$不一致的。

也就是在调制之前的m(t)的波形加上一个直流和现在的包络不是一个形式，也就无法恢复。

2. 相干解调

相干解调是很好的一个方法，也很容易理解。

相干解调先乘以载波，可以将已调信号部分$f_c$附近的的频谱进行搬移。结果是一部分信号被搬移至基带附近，另一部分则搬移至更高的频带。因为信号在基带的部分已经完全包含恢复波形的全部信息，只需要加上低通滤波器，将高频部分过滤，即可得到原信号。

由于滤波器非理想，这里使用的是巴特沃兹三阶极点的滤波器，对于恢复来说稍有一些影响。

7. 思考题

7.1 比较同步检波和包络检波的优缺点

1. 包络检波器优点：简易并且经济。使用二极管和电容可以解调。因而AM在民用广播中获得广泛应用。

2. 包络检波器缺点：仅能够解调调制系数大于等于1的AM信号，适用范围窄。

3. 同步检波优点： 适用范围广阔，能够用于多种调制信号。包括且不限于AM信号。

4. 同步检波缺点： 解调装置较为复杂，成本较包络检波高。

7.2 若调制系数大于1，是否可以用包络检波来还原

若调制系数大于1，不可以用包络检波来还原。

由波形可知，为了在解调时使用包络检波而不失真地恢复出原基带信号m(t)，也就是包络和基带信号m(t)变化情况一致。

那么就要求第一种调制方法，AM信号的包络$A_0+m(t)$总不是负的；

也就要求第二种调制方法，电路中给载波的放大增益要大于等于1，也就是调制系数要小于等于1.

因为在定义调制系数的时候，将所加上载波的括号内系数化为1，再加上a（调制系数）倍的归一化 $m_n(t)$。

那么电路中的放大增益越大，调制系数也就相应越小。

调制系数大于1，会出现“过调幅”现象，用包络检波解调时会发生失真。

7.3 调制系数分别”<1”，”>1”，”=1”时，如何计算已调信号的调制系数？

假设原先$m(t)$的振幅为$A_{max}$,载波增益为$A_{gain}$, 载波振幅为$A^{\prime }$ ,那么有：

$$\begin{gathered} A_{max}=A^{\prime }|m(t){|}_{max}+A_{gain}, \\ {A}_{min}=-A^{\prime }|m(t){|}_{max}+A_{gain}. \end{gathered}$$

调制系数的定义为：

$$a=\frac{A^{\prime }|m(t){|}_{max}}{A_{gain}}$$

因此，调制系数可以由调制后波形图中的$A_{max},A_{min}$来表示

$$a=\frac{A_{max}-Amin}{A_{max}+Amin}$$

8. 实验总结

通过AM信号调制解调实验，

我了解了AM信号的原理和两种实现方法；

了解了调幅波调制系数对于载波恢复的意义以及两种解调的方法；

分析了实验结果产生的原因，加深了对于AM调制的认识。
max} + A_{gain}.
$$

调制系数的定义为：

$$a=\frac{A^{\prime }|m(t){|}_{max}}{A_{gain}}$$

因此，调制系数可以由调制后波形图中的$A_{max},A_{min}$来表示

$$a=\frac{A_{max}-Amin}{A_{max}+Amin}$$

8. 实验总结

通过AM信号调制解调实验，

我了解了AM信号的原理和两种实现方法；

了解了调幅波调制系数对于载波恢复的意义以及两种解调的方法；

分析了实验结果产生的原因，加深了对于AM调制的认识。