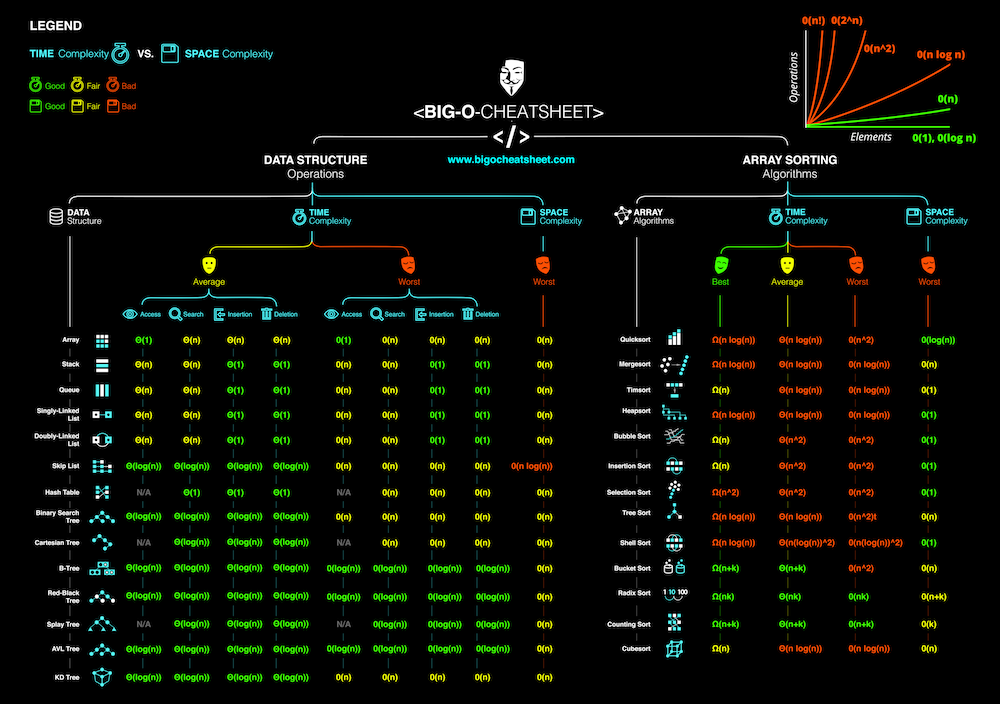
Know Thy Complexities!
https://www.bigocheatsheet.com/
Know Thy Complexities!
Hi there! This webpage covers the space and time Big-O complexities of common algorithms used in Computer Science. When preparing for technical interviews in the past, I found myself spending hours crawling the internet putting together the best, average, and worst case complexities for search and sorting algorithms so that I wouldn't be stumped when asked about them. Over the last few years, I've interviewed at several Silicon Valley startups, and also some bigger companies, like Google, Facebook, Yahoo, LinkedIn, and Uber, and each time that I prepared for an interview, I thought to myself "Why hasn't someone created a nice Big-O cheat sheet?". So, to save all of you fine folks a ton of time, I went ahead and created one. Enjoy! - Eric
Automated codebase migrations and upgrades
Big-O Complexity Chart
Horrible |
Bad |
Fair |
Good |
Excellent |
Common Data Structure Operations
| Data Structure | Time Complexity | Space Complexity | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Average | Worst | Worst | |||||||
| Access | Search | Insertion | Deletion | Access | Search | Insertion | Deletion | ||
| Array | Θ(1) |
Θ(n) |
Θ(n) |
Θ(n) |
O(1) |
O(n) |
O(n) |
O(n) |
O(n) |
| Stack | Θ(n) |
Θ(n) |
Θ(1) |
Θ(1) |
O(n) |
O(n) |
O(1) |
O(1) |
O(n) |
| Queue | Θ(n) |
Θ(n) |
Θ(1) |
Θ(1) |
O(n) |
O(n) |
O(1) |
O(1) |
O(n) |
| Singly-Linked List | Θ(n) |
Θ(n) |
Θ(1) |
Θ(1) |
O(n) |
O(n) |
O(1) |
O(1) |
O(n) |
| Doubly-Linked List | Θ(n) |
Θ(n) |
Θ(1) |
Θ(1) |
O(n) |
O(n) |
O(1) |
O(1) |
O(n) |
| Skip List | Θ(log(n)) |
Θ(log(n)) |
Θ(log(n)) |
Θ(log(n)) |
O(n) |
O(n) |
O(n) |
O(n) |
O(n log(n)) |
| Hash Table | N/A |
Θ(1) |
Θ(1) |
Θ(1) |
N/A |
O(n) |
O(n) |
O(n) |
O(n) |
| Binary Search Tree | Θ(log(n)) |
Θ(log(n)) |
Θ(log(n)) |
Θ(log(n)) |
O(n) |
O(n) |
O(n) |
O(n) |
O(n) |
| Cartesian Tree | N/A |
Θ(log(n)) |
Θ(log(n)) |
Θ(log(n)) |
N/A |
O(n) |
O(n) |
O(n) |
O(n) |
| B-Tree | Θ(log(n)) |
Θ(log(n)) |
Θ(log(n)) |
Θ(log(n)) |
O(log(n)) |
O(log(n)) |
O(log(n)) |
O(log(n)) |
O(n) |
| Red-Black Tree | Θ(log(n)) |
Θ(log(n)) |
Θ(log(n)) |
Θ(log(n)) |
O(log(n)) |
O(log(n)) |
O(log(n)) |
O(log(n)) |
O(n) |
| Splay Tree | N/A |
Θ(log(n)) |
Θ(log(n)) |
Θ(log(n)) |
N/A |
O(log(n)) |
O(log(n)) |
O(log(n)) |
O(n) |
| AVL Tree | Θ(log(n)) |
Θ(log(n)) |
Θ(log(n)) |
Θ(log(n)) |
O(log(n)) |
O(log(n)) |
O(log(n)) |
O(log(n)) |
O(n) |
| KD Tree | Θ(log(n)) |
Θ(log(n)) |
Θ(log(n)) |
Θ(log(n)) |
O(n) |
O(n) |
O(n) |
O(n) |
O(n) |
Array Sorting Algorithms
| Algorithm | Time Complexity | Space Complexity | ||
|---|---|---|---|---|
| Best | Average | Worst | Worst | |
| Quicksort | Ω(n log(n)) |
Θ(n log(n)) |
O(n^2) |
O(log(n)) |
| Mergesort | Ω(n log(n)) |
Θ(n log(n)) |
O(n log(n)) |
O(n) |
| Timsort | Ω(n) |
Θ(n log(n)) |
O(n log(n)) |
O(n) |
| Heapsort | Ω(n log(n)) |
Θ(n log(n)) |
O(n log(n)) |
O(1) |
| Bubble Sort | Ω(n) |
Θ(n^2) |
O(n^2) |
O(1) |
| Insertion Sort | Ω(n) |
Θ(n^2) |
O(n^2) |
O(1) |
| Selection Sort | Ω(n^2) |
Θ(n^2) |
O(n^2) |
O(1) |
| Tree Sort | Ω(n log(n)) |
Θ(n log(n)) |
O(n^2) |
O(n) |
| Shell Sort | Ω(n log(n)) |
Θ(n(log(n))^2) |
O(n(log(n))^2) |
O(1) |
| Bucket Sort | Ω(n+k) |
Θ(n+k) |
O(n^2) |
O(n) |
| Radix Sort | Ω(nk) |
Θ(nk) |
O(nk) |
O(n+k) |
| Counting Sort | Ω(n+k) |
Θ(n+k) |
O(n+k) |
O(k) |
| Cubesort | Ω(n) |
Θ(n log(n)) |
O(n log(n)) |
O(n) |
Learn More
- Cracking the Coding Interview: 150 Programming Questions and Solutions
- Introduction to Algorithms, 3rd Edition
- Data Structures and Algorithms in Java (2nd Edition)
- High Performance JavaScript (Build Faster Web Application Interfaces)
Get the Official Big-O Cheat Sheet Poster
