记录一下哈希表底层原理
理解HashMap底层，首先应该理解Hash函数
从解决一个问题入手：大量的数据要存储查询，构造哈希表来解决
初步想法
借鉴数组下标访问的思路来做，只需知道起始位置和下标值，
不管数组中有多少个元素，都可以一次访问到，
将元素和元素位置建立一种一一对应的关系
Hash函数的出现
输入的元素的范围可能很大甚至无穷，而我们的内存有限，
所以说我们需要一种函数映射关系，将这些无限的元素映射到我们有限的内存地址上。
Hash函数代表着一类函数，即把任意范围的元素可以通过映射关系压缩成固定范围的元素。
Hash函数的选择
如果是正整数，我们可以用这个正整数数除以某个数，取其余数，即我们常用的 k % m，k为正整数，m 为除数；
这样一来，范围就缩小了很多，比如说 15%10=5,26%10=6,...,所有的正整数经过运算，都变成了 0-9 范围之间的数了，
这样范围就缩小了很多
m 的选择
这种做法，m 的选择就非常重要了，如果 k 值分布均匀还无所谓，如果 k 值具有某些特征
比如说 k 的个位基本上不变，而高位分布均匀，如 15,25,45,65,85,95,155，就遭遇大冲突了，
必须要使得经过Hash函数后关键字的分布均匀，尽量减少冲突
链地址法
为了解决冲突，引出链地址法
在存储的时候，如果多个元素被Hash到同一位置，那么就加入到该位置所指向的链表中，
如果该位置没有元素，则为null(指向空)”
由于新加入的元素很可能被再次访问到，使用“头插”
rehash
这样解决冲突固然好，但是也有瓶颈
当我们实际存入的值越来越多的时候，这个链表也势必越来越长，
那当我们进行查找的时候，势必就会遍历链表，效率也就越来越慢。
因此，我们要选取一个相关的新的Hash函数（比如之前使用 key % m，现在只改变一下m的值）
将旧Hash表中所有的元素通过新的Hash函数计算出新的Hash值，并将其插入到新表中（仍然使用链表），这就叫rehash
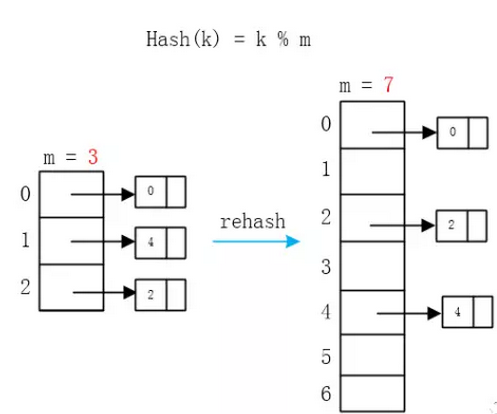
这里的数组就扩大了近两倍，由于要大小要选素数，那就选原数组大小两倍后的第一个素数7，旧Hash表和新Hash表采用了不同的Hash函数，但相关，只是m的取值变了
装载因子 α
我们可以定义这样一个变量 α = 所有元素个数/数组的大小，
它代表着我们的Hash表（也就是数组）的装满程度，在这里也代表链表的平均长度
这个装载因子代表了Hash表的装满程度，这里也可以代表链表的平均长度，那么也就可以代表查询时的时间长短了。
