python数据结构之树(二分查找树)
本篇学习笔记记录二叉查找树的定义以及用python实现数据结构增、删、查的操作。
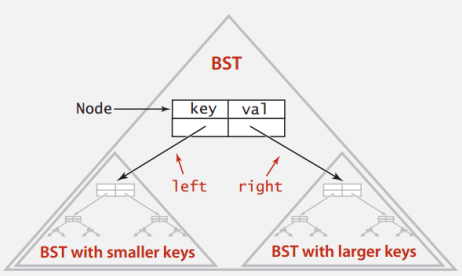
二叉查找树(Binary Search Tree)
简称BST,又叫二叉排序树(Binary Sort Tree),是对称顺序的二叉树,支持多种动态集合操作。
二叉树也是:
- 空
- 两个不相交的二叉树(左和右)
对称顺序
- 每个节点都有一个密钥,每个节点的密钥都是
- 大于其左侧子树中的所有密钥
- 小于其右侧子树中的所有密钥
BST 用Python表示
BST是对根节点的引用
节点由四个字段组成
- 一个 Key 和 一个 Value
- 对左子树(较小的密钥)和右子树(较大的密钥)的引用
class Node(object): __slots__ = '_item' , '_lchild' , '_rchild' def __init__ (self, item, lchild=None, rchild=None): self._item = item self._lchild = lchild self._rchild = rchild
BST操作方法
- BST 搜索
- BST 插入
- BST获取最小值与最大值
- BST 删除
BST 搜索
- 获取:返回给定键对应的值;如果没有这样的键,则返回null
- 成本:比较的数量等于1 +节点的深度
# Get树元素的方法 def get(self, key): return self.__get(self._root, key); def __get(self, node, key): # helper if (node is None): return None if (key == node._item): return node._item if (key < node._item): return self.__get(node._lchild, key) else: return self.__get(node._rchild, key)
BST 插入
添加:将关联值与关键字关联
搜索密钥,然后搜索两个案例
- 键入树⇒重置值
- 密钥不在树中⇒添加新节点
成本:比较的数量等于1 +节点的深度
# add元素的方法 def add(self, value): self._root = self.__add(self._root, value) def __add(self, node, value): # return node ,helper if (node is None): return Node(value) if (value == node._item): pass else: if (value < node._item): node._lchild = self.__add(node._lchild, value) else: node._rchild = self.__add(node._rchild, value) return node
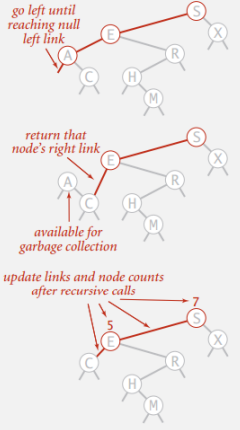
BST 删除
最复杂的二叉搜索树操作
我们必须确保当我们移除一个元素时,我们维护二叉 搜索树属性
删除最小密钥
- 向左移动直到找到带有空左链接的节点
- 用正确的链接替换该节点
- 更新子树计数
# remove树元素的方法 def remove(self, key): self._root = self.__remove(self._root, key) def __remove(self, node, key): # helper if node is None: return None if (key < node._item): node._lchild = self.__remove(node._lchild, key) elif (key > node._item): node._rchild = self.__remove(node._rchild, key) else: if (node._lchild is None): node = node._rchild # if rchild is None, node = None; case 1: no child # if rchild is not None, node = node._rchild; case 2: one child elif (node._rchild is None): node = node._lchild else: node._item = self.__get_max(node._lchild) node._lchild = self.__remove(node._lchild, node._item) return node
BST获取最小值与最大值

# get max 元素的方法 def get_max(self): return self.__get_max(self._root) def __get_max(self, node): # helper if (node is None): return None while (node._rchild is not None): node = node._rchild return node._item
Github地址:https://github.com/kumataahh


