python数据结构之树（概述）

树

在计算机科学中,树是分层结构的抽象模型 。本篇学习笔记记录树的内容如下：

树的基本功能：定义、术语、ADT

树的遍历方法：前序、中序、后序

树的定义

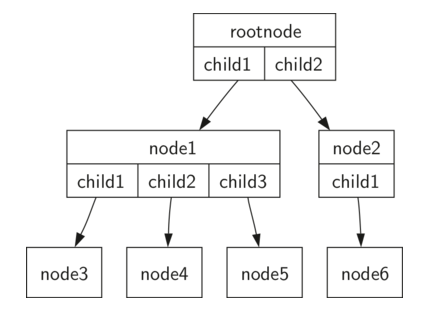
第一种：树由一组节点和一组连接节点的边组成。树具有以下属性：

• 树的一个节点被指定为根节点。
• 除了根节点之外，每个节点 n 通过一个其他节点 p 的边连接，其中 p 是 n 的父节点。
• 从根路径遍历到每个节点路径唯一。
• 如果树中的每个节点最多有两个子节点，我们说该树是一个二叉树。

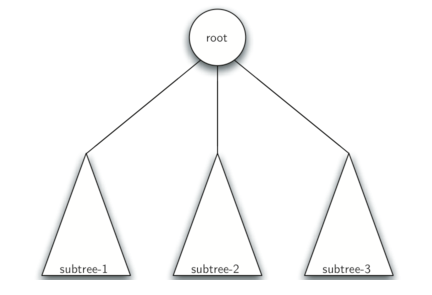
第二种：树是空的，或者由一个根节点和零个或多个子树组成，每个子树也是一棵树。每个子树的根节点通过边连接到父树的根节点。

下图说明了树的这种递归定义。使用树的递归定义，我们知道图中的树至少有四个节点，因为表示一个子树的每个三角形必须有一个根节点。

它可能有比这更多的节点，但我们不知道，除非我们更深入树。

树的术语

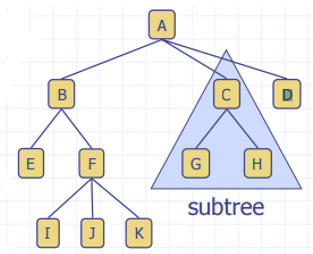
• 根节点（Root）：无父节点 (A)
• 中间节点（Internal node）：具有至少一个子节点的节点 (A, B, C, F)
• 叶子（External node）：无子节点 (E, I, J, K, G, H, D)
• 祖先（Ancestors）：:父母,祖父母,祖父母,等等
• 后代（Descendant）：孩子,孙子,重孙子,等等.
• 深度（Depth of a node）：树的祖先高度数：任意节点的最大深度. Depth(E) = 2
• 高度（Height）：Height = 3
• 兄弟姐妹（Sibling）：C是B和D的兄弟姐妹.
• 子树（Subtree）：树由节点及其后代组成
• 边（Edge of tree）：边是树的另一个基本部分。边连接两个节点以显示它们之间存在关系。每个节点（除根之外）都恰好从另一个节点的传入连接。每个节点可以具有多个输出边。
• 通路（Path）：路径是由边连接节点的有序列表。如I到G的Path： I->F->B->A->C->G

树的ADT

• 二叉树可以通过存储一个节点的数据加两个子指针来实现.
• 具有两个以上孩子的树可以使用链接的节点列表来实现

通用方法:

• Int size()
• boolean isEmpty()
• Iterator elements()
• Iterator positions()

 查询方法:

• boolean isInternal(p)
• boolean isExternal(p)
• boolean isRoot(p)

更新方法:

• object replace (p, o)

访问器方法:

• Node root()
• Node parent(p)
• List children(p) 

 树的遍历方法

有三种常用的模式来访问树中的所有节点。这些模式之间的差异是每个节点被访问的顺序。我们称这种访问节点方式为“遍历”。

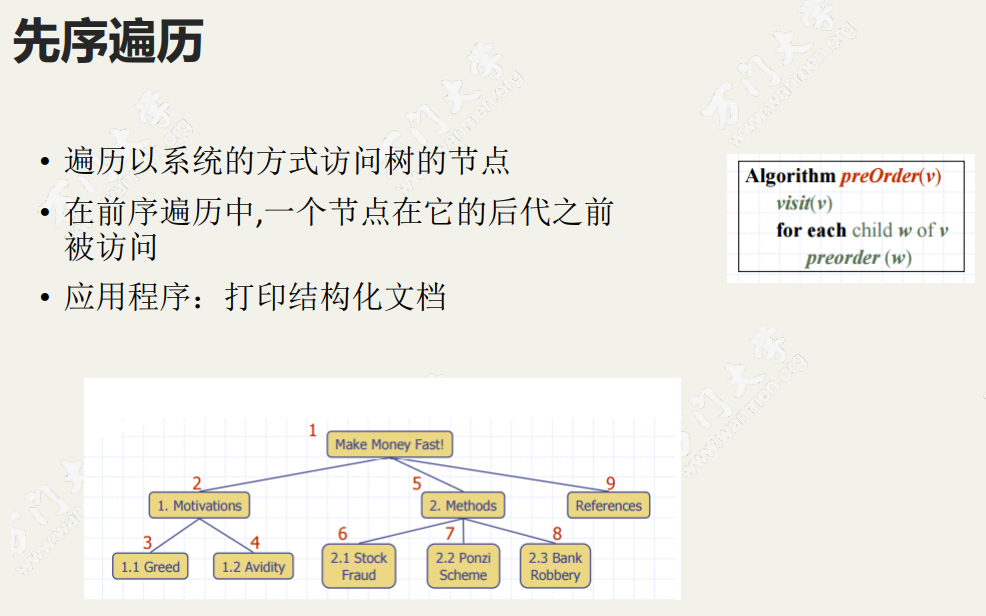
• 先序： 在前序遍历中，我们首先访问根节点，然后递归地做左侧子树的前序遍历，随后是右侧子树的递归前序遍历。
• 中序（顺序遍历）：在一个中序遍历中，我们递归地对左子树进行一次遍历，访问根节点，最后递归遍历右子树。
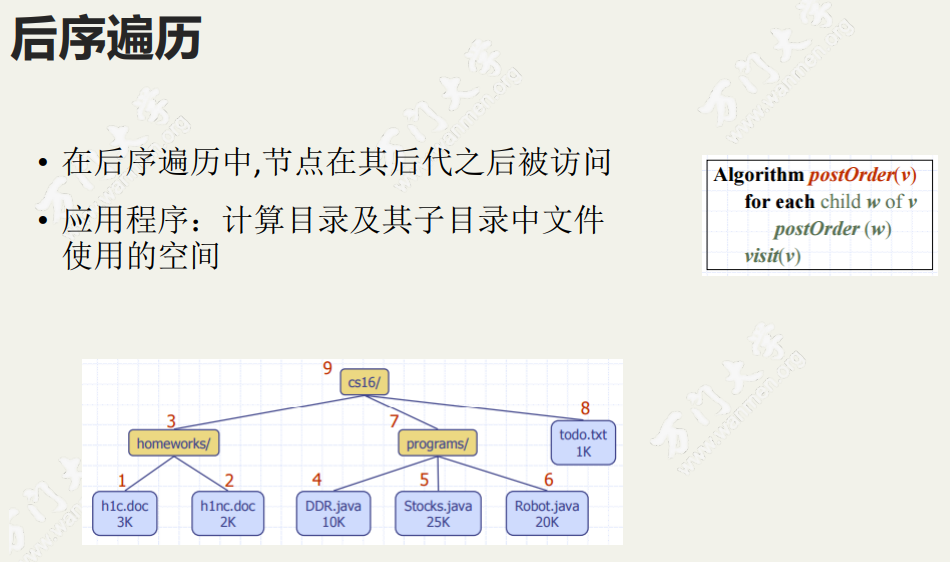
• 后序：在后序遍历中，我们递归地对左子树和右子树进行后序遍历，然后访问根节点。