归并排序之python

归并排序( Merge sort），也成合并排序、二分排序

归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为2-路归并。 

1.算法描述：

• 分而治之
• 分 ：

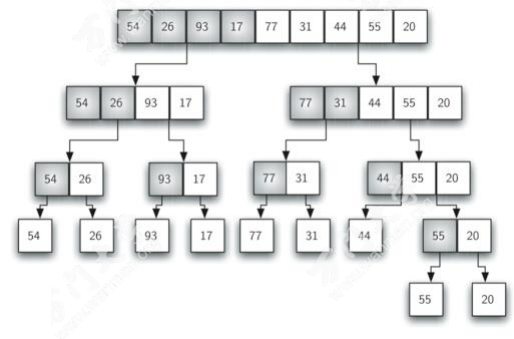
1. 　　递归地拆分数组,直到它被分成两对单个元素数组为止.
2. 　　然后,将这些单个元素中的每一个与它的对合并,然后将这些对与它们的对等合并， 直到整个列表按照排序顺序合并为止.

• 治 ：

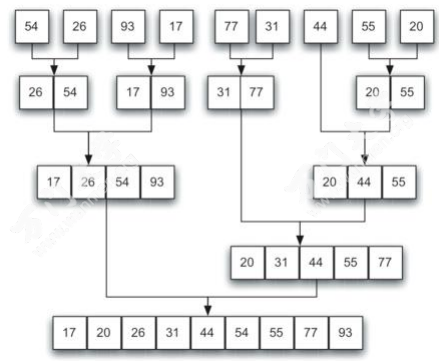
1. 　　将2个排序列表合并为另一个排序列表是很简单的.
2. 　　简单地通过比较每个列表的头,删除最小的,以加入新排序的列表. 
3. 　　O(n) 操作

2.算法属性:

• 时间复杂度：O(nlogn)
• 空间复杂度：O(1)
• 稳定性：稳定

3.代码实现

'''
名字很多：归并排序/合并排序/二分排序
算法时间复杂度 O(logn)
递归
两个步骤：1.拆分 2.合并
'''
def merge_sort(nums=list):
    #取mid以及左右两个数组
    mid = len(nums)//2
    left_nums,right_nums = nums[:mid],nums[mid:]

    #递归分治
    if len(left_nums) > 1:
        left_nums = merge_sort(left_nums)
    if len(right_nums) > 1:
        right_nums = merge_sort(right_nums)

    #合并
    res = []
    while left_nums and right_nums:  #两个都不为空的时候
        if left_nums[-1] >= right_nums[-1]:  #尾部较大者
            res.append(left_nums.pop())
        else:
            res.append(right_nums.pop())
    res.reverse() #倒序
    return (left_nums or right_nums) + res #前面加上剩下的非空nums

lis = [7, 5, 0, 6, 3, 4, 1, 9, 8, 2]
print(merge_sort(lis)) #[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

 

#学习版本
#递归
#两个步骤：1.拆分 2.合并

def _merge(a: list, b: list) -> list:
    #合并两个排序表
    c = []
    while len(a) > 0 and len(b) > 0:
        if a[0] < b[0]:
            c.append(a[0])
            a.remove(a[0])
        else:
            c.append(b[0])
            b.remove(b[0])

    if len(a) == 0:
        c += b
    else:
        c += a
    return c


def _merge_sorted(nums: list) -> list:
    # Won't sort in place
    if len(nums) <= 1:
        return nums

    m = len(nums) // 2
    a = _merge_sorted(nums[:m])     #前半
    b = _merge_sorted(nums[m:])　　　#后半
    return _merge(a, b)


# Wrapper包装器
def merge_sorted(nums: list, reverse=False) -> list:
    import time
    start = time.time()
    #归并排序
    nums = _merge_sorted(nums)
    if reverse:
        nums = nums[::-1]

    t = time.time() - start
    return nums, len(nums), t

lis = [1, 3, 5, 7, 9, 2, 4, 6, 8, 0]
merge_sorted(l, reverse=False)[0]

#输出结果
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]