计数排序之python

计数排序( Count sort）

一个不需要比较的，类似于桶排序的线性时间排序算法。该算法是对已知数量范围的数组进行排序。其时间复杂度为O(n)，适用于小范围集合或重复元素多的排序。计数排序是用来排序0到100之间的数字的最 
好的算法。

1.算法描述：

“抽屉原理”

• 找出待排序的数组中最大和最小的元素；
• 统计数组中每个值为i的元素出现的次数，存入数组C的第i项；
• 对所有的计数累加（从C中的第一个元素开始，每一项和前一项相加）；
• 反向填充目标数组：将每个元素i放在新数组的第C(i)项，每放一个元素就将C(i)减去1。

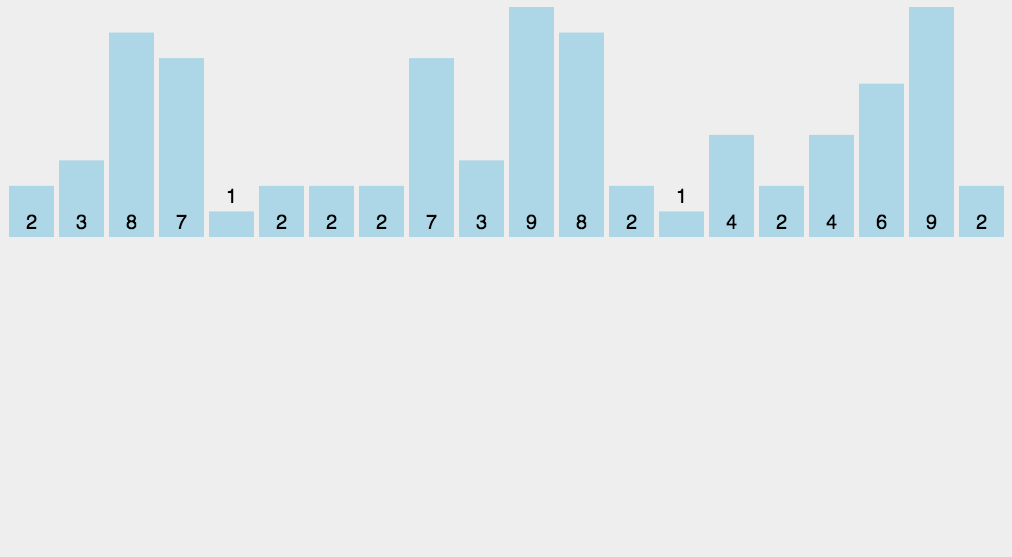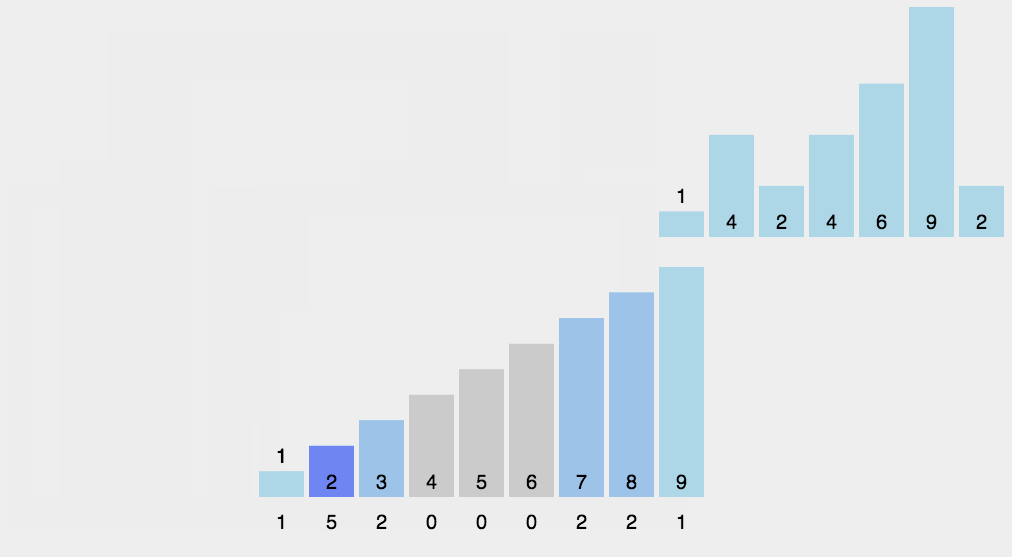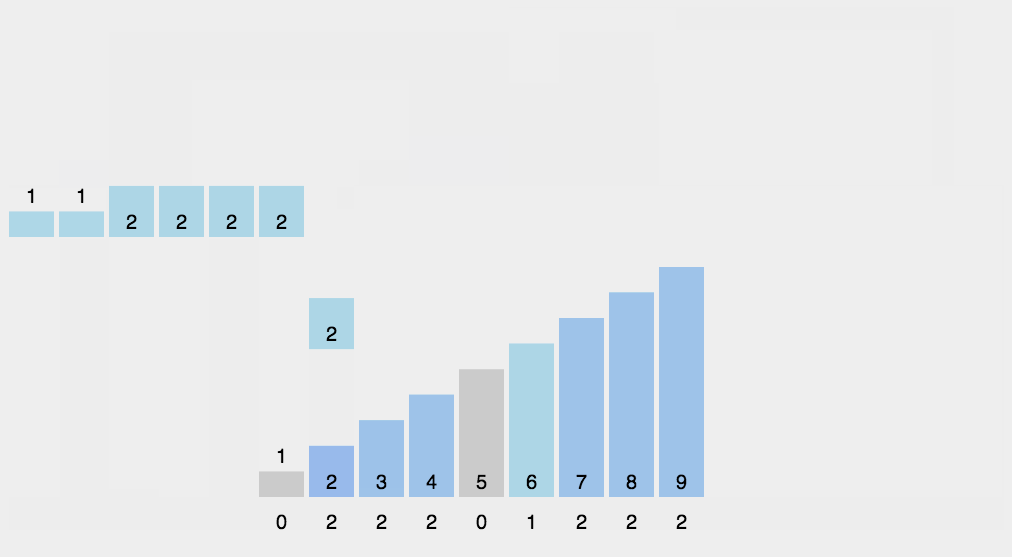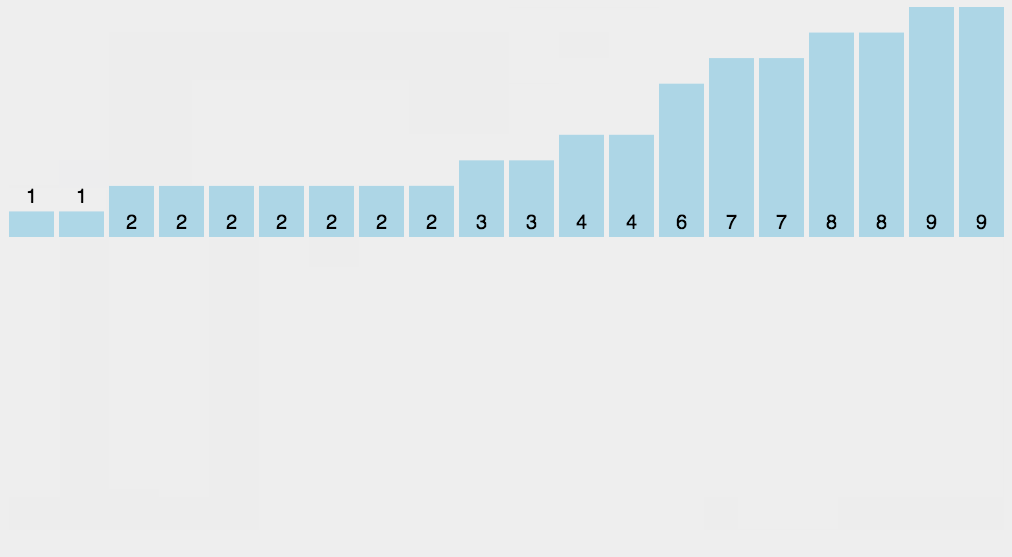
2.算法属性:

• 稳定性：不稳定
• 时间复杂度：O(n)
• 空间复杂度：O(M)

3.代码实现

#时间复杂度O(n)
#kumata 's code
'''
三个步骤：
1.找出最大最小值  
2.根据最大最小值差制造抽屉，把元素放进“抽屉”
3.把“抽屉”里面的元素拿出来重新排列
'''
import time
def count_sort(nums):
    start = time.time()    
    mmax, mmin = nums[0], nums[0]
    
    #第一个for循环找到最大值和最小值
    for i in range(1, len(nums)):
        if (nums[i] > mmax): 
            mmax = nums[i]
        elif (nums[i] < mmin): 
            mmin = nums[i]
    print('最大值:',mmax)
    print('最小值:',mmin)
    
    #“发抽屉”，制造多少个抽屉
    drawer = mmax - mmin + 1
    
    #刚开始抽屉里全部都是0
    counts = [0] * drawer
    print('抽屉数：',counts)   
    
    #通过index把元素往抽屉里面放
    for i in range (len(nums)):
        counts[nums[i] - mmin] = counts[nums[i] - mmin] + 1

    #把抽屉里面的元素拿出来重新排列
    #第一个for循环为抽屉的大小，第二个为抽屉里每个元素的个数，所以时间复杂度实为O(n)
    pos = 0
    for i in range(drawer):      
        for j in range(counts[i]):
            nums[pos] = i + mmin
            pos += 1
            
    t = time.time() - start
    return nums, t

#输出结果
最大值: 45
最小值: 1
抽屉数： [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]

([1, 2, 3, 4, 5, 6, 8, 11, 22, 45], 0.0005011558532714844)