查找算法：顺序查找与二分法查找

查找（Search）

描述顺序查找与二分法（折半搜索）的概念以及用python实现其查找流程

笔记中二分法记录简单的检索方法，更详细方法传送门：二分法查找的python案例

顺序查找

算法原理：遍历数据元素

查找表类型：无序表查找，也就是数据不sort的线性查找，遍历数据元素

算法分析：

 

由此最终算法时间复杂度为O(n)

 

# 最常见的就是for遍历列表的顺序查找算法
# 时间复杂度O(n)
#Question: Given a sorted list of numbers, find the index of a specific value in the list. If no such value, return -1.

def sequential_search(lis, key):
    for i in range(len(lis)):
        if lis[i] == key:
            return i
    else:               #注意else的缩进位置，与if并列的话都会返回False
        return False

alist = [1, 5, 8, 123, 22, 54, 7, 99, 300, 222] 
result = sequential_search(alist, 123)
print(result)

#输出结果
3

 

二分法

算法原理：在查找表中不断取中间元素与查找值进行比较，以二分之一的倍率进行表范围的缩小。

查找表类型：有序表查找，查找表中的数据必须按某个主键进行某种排序。

算法分析：

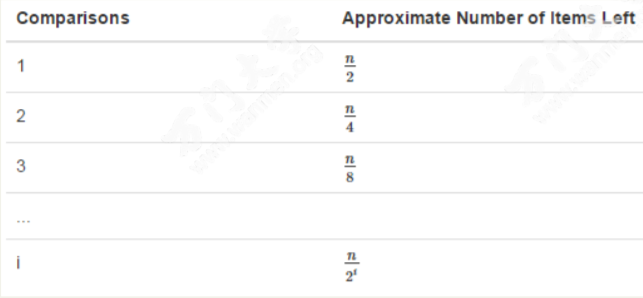
由此可得算法时间复杂度为O(logn)，比O(n)更优

 

'''
简单方法
二分法查找在列表中的用户输入值，返回index
三种情况跳出循环体： LR相邻    LR位置重合   RL
算法时间复杂度为O(logn)

'''

def bi_search(lis,num):
    
    if len(lis) == 0:           #判断边界条件
        return -1
　　
    left, right = 0, len(lis)-1          #列表的起始点和终点
  
    while left <= right:

        mid = (left + (right - left)) // 2     #取二分中心点，或 mid = (left + right) // 2

        if num < lis[mid]:               #右点左移
            right = mid - 1 
        elif num > lis[mid]:             #左点右移
            left = mid + 1 
        else:                            #num == lis[mid]    
            return mid

    return -1

num = int(input('please input a num:'))
alist = [1,2,3,4,5,6,7,8]
bi_search(alist,num)

输出结果：
please input a num:3
2    

改进方案：如果我要找一个数组中相同数字最前面的那个数字。比如lis = [1,2,2,2,2,3,3,5,6],用上面的代码会返回index为4，下面代码解决如何返回相同元素的最前一个

'''
改进版本经典方法，这种方法更加好写
把常规方法的right = mid -1 和left = mid +1修改
找不到返回-1
'''

def bi_search2(lis, num):
   
    #这个程序中这一条判断边界非常重要
    if len(lis) == 0:
        return -1
    
    #判断二分条件
    left, right = 0, len(lis) - 1
    while left + 1 < right:
        mid = left + (right - left) // 2
        if lis[mid] == num:
            right = mid
        elif lis[mid] < num:
            left = mid
        elif lis[mid] > num:
            right = mid
    
    #在这里返回
    if lis[left] == num:
        return left
    if lis[right] == num:
        return right
    
    return -1


num = int(input('please input a num:'))
alist = [1,2,2,2,2,6,7,8]
bi_search2(alist,num)

#输出结果
please input a num: 2
1