算法概念

算法 ( Algorithm )

一、功能: 有限时间内解决问题的一系列清晰指令

二、效率 

• 空间
• 时间

三、目标

• 能够识别程序要求的功能以解决当前任务设计
• 能够高效解决此任务的数据结构与算法
• 评价该方案的效率和正确性

算法分析

运行时间 (时间复杂度) 

1. 运行时间会随着输入的大小如何变化 
2. 最好的情况: 运行时间的上限 (最少运行时间) 由最简单的输入决定 提供了所有输入的最终优化目标 
3. 最差的情况:运行时间的下限 (最多运行时间) 由最复杂的输入决定 提供了所有输入的保障时间 
4. 平均情况: 随机输入的运行时间的期望 需要建立随机输入的模型 是一种评价算法表现的方法 
5. 平均情况时间通常很难测定 ，我们通常情况下关注最差情况下的运行时间

 可以看出，运行时间的效率从高到低的排序为：

Constant （常数的）> Logarithmic（对数的） > Linear（线性的） > N-log-N（N对数N） > Guadratic（二次方的） > Exponential（指数的） > Cubic（三次方的）

人类描述：

O(1) > O(logn) > O(n) > O(nlogn) > O(n^2) > O(n^3) > O(2^n) > O(n!) > O(n^n) 

 

评估算法运行时间

算法 arrayMax 在最差情况下执行了 8n − 3 个基本操作。

定义:

a = 最快的基本操作所需要的运行时间

b = 最慢的基本操作所需要的运行时间

令 T (n) 为 arrayMax 的运行时间。

则应该有：

a (8n − 3) ≤ T (n) ≤ b (8n − 3)

因此，运行时间 T (n) 由两条线性函数所划定其范围

 

近似记法

Big - O 记法

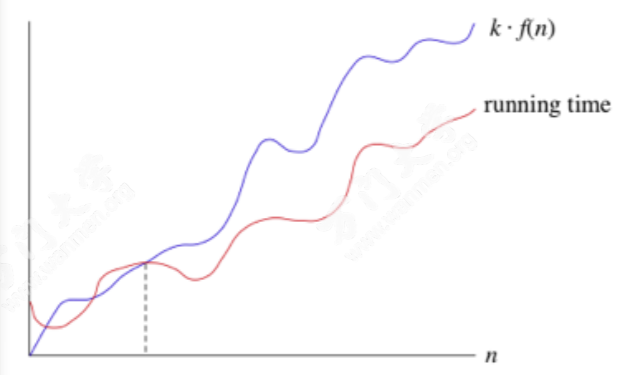
一般习惯用 Θ (n) 记法来 渐进界定算法运行 时间的常数函数边界。有时，我们只希望这 个常数函数代表算法运行时间的上界。

尽管在最差情况下二分法搜索的运行时间为 Θ (lgn)，认为在所有情况下二分法搜索的搜 索时间为 Θ (lgn) 是错误的。

二分法搜索的时间从来不会超过 Θ (lgn)， 多数情况下其搜索时间都会少于Θ (lgn)

 

时间复杂度

一般情况下，算法中基本操作重复执行的次数是问题规模n的某个函数，用T(n)表示，若有某 个辅助函数f(n) ，使得当n趋近于无穷大时

T(n)/f(n)的极限值为不等于零的常数，则称 f(n)是T(n)的同数量级函数。 记作T(n)=Ｏ(f(n)),称Ｏ(f(n)) 为算法的渐进时间复杂度，简称时间复杂度

 

#一般我们根据时间复杂度来判断该算法的时间效率
#举例说明

for (n):
    xxxxxxx
#这种为常见的O（n）

for (n):
    for(m):
        xxxxxx
#这种为O（n×m）
#若嵌套的两条程度同级别可视为 O（n^2）

for (n):
    xxxxxxx
for (n):
    xxxxxxx
#这种为O（n）+O（n），也为O（n）

 

附上Python内置方法时间复杂度的学习链接：

https://www.cnblogs.com/harvey888/p/6659061.html   

 

三大算法概述

• 分治法
• 动态规划
• 贪婪算法

一、分治法

 

基本思想：

      将一些难以解决的大问题分割成规模较小的相同问题，对于一个问题规模为n的问题，如果能直接解决，则解决，否则将其拆开，

 

分治法适用的情况：

 

  分治法所能解决的问题一般具有以下几个特征：

  1) 该问题的规模缩小到一定的程度就可以容易地解决

  2) 该问题可以分解为若干个规模较小的相同问题，即该问题具有最优子结构性质

  3) 利用该问题分解出的子问题的解可以合并为该问题的解

  4) 该问题所分解出的各个子问题是相互独立的，即子问题之间不包含公共的子子问题。

 

第一条特征是绝大多数问题都可以满足的，因为问题的计算复杂性一般是随着问题规模的增加而增加；

第二条特征是应用分治法的前提它也是大多数问题可以满足的，此特征反映了递归思想的应用；、

第三条特征是关键，能否利用分治法完全取决于问题是否具有第三条特征，如果具备了第一条和第二条特征，而不具备第三条特征，则可以考虑用贪心法或动态规划法。

第四条特征涉及到分治法的效率，如果各子问题是不独立的则分治法要做许多不必要的工作，重复地解公共的子问题，此时虽然可用分治法，但一般用动态规划法较好。

 

可使用分治法求解的一些经典问题：

（1）二分搜索

（2）大整数乘法

（3）Strassen矩阵乘法

（4）棋盘覆盖

（5）合并排序

（6）快速排序

（7）线性时间选择

（8）最接近点对问题

（9）循环赛日程表

（10）汉诺塔

 

二、动态规划

 

基本思想：

将待求的问题分解为若干状态，下一状态依靠上一状态来决定，而分治则是将为问题分成若干子问题，子问题之间是独立的。并且动规的问题是 某个状态以后的状态不影响之前的状态，只与当前的状态有关，一定要清楚你当前解决的问题是怎么来的，时候怎么通过一步步到现在的状态，清楚上一步的状态的所有可能，然后再写出在这一步中所有可能做出的决定，判断当前决策，问题就可以轻松的解决啦；

 

求解的基本步骤：

       动态规划所处理的问题是一个多阶段决策问题，一般由初始状态开始，通过对中间阶段决策的选择，达到结束状态。这些决策形成了一个决策序列，同时确定了完成整个过程的一条活动路线(通常是求最优的活动路线)。如图所示。动态规划的设计都有着一定的模式，一般要经历以下几个步骤。

 初始状态→│决策１│→│决策２│→…→│决策ｎ│→结束状态

  (1)划分阶段：按照问题的时间或空间特征，把问题分为若干个阶段。在划分阶段时，注意划分后的阶段一定要是有序的或者是可排序的，否则问题就无法求解。

  (2)确定状态和状态变量：将问题发展到各个阶段时所处于的各种客观情况用不同的状态表示出来。当然，状态的选择要满足无后效性。

  (3)确定决策并写出状态转移方程：因为决策和状态转移有着天然的联系，状态转移就是根据上一阶段的状态和决策来导出本阶段的状态。所以如果确定了决策，状态转移方程也就可写出。但事实上常常是反过来做，根据相邻两个阶段的状态之间的关系来确定决策方法和状态转移方程。

  (4)寻找边界条件：给出的状态转移方程是一个递推式，需要一个递推的终止条件或边界条件。 一般，只要解决问题的阶段、状态和状态转移决策确定了，就可以写出状态转移方程（包括边界条件）。

 

实际应用中可以按以下几个简化的步骤进行设计：

    （1）分析最优解的性质，并刻画其结构特征。

    （2）递归的定义最优解。

    （3）以自底向上或自顶向下的记忆化方式（备忘录法）计算出最优值

    （4）根据计算最优值时得到的信息，构造问题的最优解

 

算法实现的说明：

    动态规划的主要难点在于理论上的设计，也就是上面4个步骤的确定，一旦设计完成，实现部分就会非常简单。

     使用动态规划求解问题，最重要的就是确定动态规划三要素：

    （1）问题的阶段 （2）每个阶段的状态

    （3）从前一个阶段转化到后一个阶段之间的递推关系。

     递推关系必须是从次小的问题开始到较大的问题之间的转化，从这个角度来说，动态规划往往可以用递归程序来实现，不过因为递推可以充分利用前面保存的子问题的解来减少重复计算，所以对于大规模问题来说，有递归不可比拟的优势，这也是动态规划算法的核心之处。

    确定了动态规划的这三要素，整个求解过程就可以用一个最优决策表来描述，最优决策表是一个二维表，其中行表示决策的阶段，列表示问题状态，表格需要填写的数据一般对应此问题的在某个阶段某个状态下的最优值（如最短路径，最长公共子序列，最大价值等），填表的过程就是根据递推关系，从1行1列开始，以行或者列优先的顺序，依次填写表格，最后根据整个表格的数据通过简单的取舍或者运算求得问题的最优解。

          f(n,m)=max{f(n-1,m), f(n-1,m-w[n])+P(n,m)}

 

三、贪心算法

       

      基本思想：在解决一个问题的时候，总是使用当前最优的选择，且该选择无法改变，和动规相同，贪心算法具有无后效性的特点，后面的状态的改变无法影响之前已经做出决策的状态，贪心和动规有一个很明显的不同可以理解为动规是将问题逐渐分解的，首先分解为上一个状态，再又上个状态分解为上上个状态，而贪心则是，先走出第一步然后做出当前最优选择，再走出第二步。

 

贪心算法的基本思路：

    1.建立数学模型来描述问题。

    2.把求解的问题分成若干个子问题。

    3.对每一子问题求解，得到子问题的局部最优解。

    4.把子问题的解局部最优解合成原来解问题的一个解。

 

贪心算法适用的问题：

      贪心策略适用的前提是：局部最优策略能导致产生全局最优解。

    实际上，贪心算法适用的情况很少。一般，对一个问题分析是否适用于贪心算法，可以先选择该问题下的几个实际数据进行分析，就可做出判断。

 

贪心算法的实现框架：

    从问题的某一初始解出发；

    while （能朝给定总目标前进一步）

    { 

          利用可行的决策，求出可行解的一个解元素；

    }

    由所有解元素组合成问题的一个可行解；

  

贪心策略的选择：

     因为用贪心算法只能通过解局部最优解的策略来达到全局最优解，因此，一定要注意判断问题是否适合采用贪心算法策略，找到的解是否一定是问题的最优解。