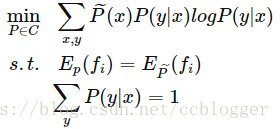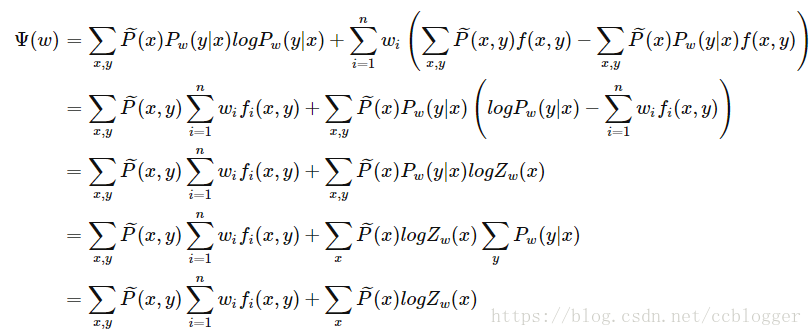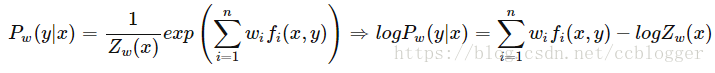基于条件概率分类的算法--最大熵模型

关于使用拉格朗日对偶求解最优解问题详解:
最大熵模型:
给定数据集
,特征函数 fi(x,y),i=1,2…,n,根据经验分布得到满足约束集的模型集合 C :
MaxEnt 模型的求解
MaxEnt 模型最后被形式化为带有约束条件的最优化问题,可以通过拉格朗日乘子法将其转为无约束优化的问题,引入拉格朗日乘子:
, 定义朗格朗日函数 L(P,w):
现在问题转化为: ,拉格朗日函数 L(P,w) 的约束是要满足的 ,如果不满足约束的话,只需令
,则可得
,因为需要得到极小值,所以约束必须要满足,满足约束后可得:
,现在问题可以形式化为便于拉格朗日对偶处理的极小极大的问题:
由于 L(P,w)是关于 P 的凸函数,根据拉格朗日对偶可得 L(P,w)的极小极大问题与极大极小问题是等价的:
现在可以先求内部的极小问题得到的解为关于 w 的函数,可以记做 Ψ(w) :
上式的解 可以记做:
由于求解 P的最小值,只需对于 P(y|x) 求导即可,令导数等于 0 即可得到
:
由于 ,可得:
进而可以得到:
这里 起到了归一化的作用,令
表示
,便得到了 MaxEnt 模型 :
这里代表特征函数,
代表特征函数的权值,
即为 MaxEnt 模型,现在内部的极小化求解得到关于 w的函数,现在求其对偶问题的外部极大化即可,将最优解记做
:
所以现在最大上模型转为求解 的极大化问题,求解最优的
后, 便得到了所要求的MaxEnt 模型,将
带入
,可得:
以上推倒第二行到第三行用到以下结论:
倒数第二行到最后一行是由于:,最终通过一系列极其复杂的运算,得到了需要极大化的式子:
LR与最大熵的等价性:(对比二者公式即可, 倒数第二个公式既是sigmoid模型形式)
逻辑回归跟最大熵模型没有本质差别。逻辑回归是最大熵相应类别为二类时的特殊情况
二项式分布的最大熵解等价于二项式指数形式(sigmoid)的最大似然;
多项式分布的最大熵等价于多项式分布指数形式(softmax)的最大似然
二者都称为对数线性模型