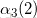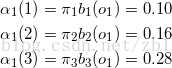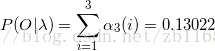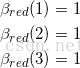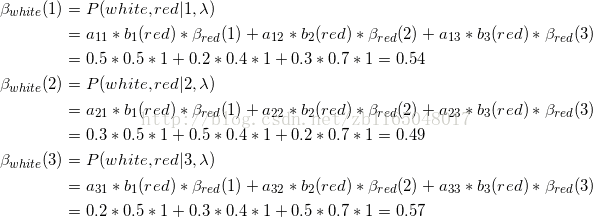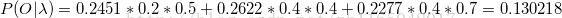前向-后向算法实例
已知HMM模型参数:
转移概率矩阵A:
| 0.5 | 0.2 | 0.3 |
| 0.3 | 0.5 | 0.2 |
| 0.2 | 0.3 | 0.5 |
| 0.5 | 0.5 |
| 0.4 | 0.6 |
| 0.7 | 0.3 |
π=(0.2 , 0.4 , 0.4)
求解:三次取球颜色为(红、白、红)的概率P(O|λ)
提示:盒子相当于三种隐状态,两种颜色的球相当于观测情况,观测序列由(红、白、红)给出
(1)计算初值
a1(2) 代表第一个时间下, 从第二个盒子里取出红球的概率
(2)递推计算
(3)终止条件
关于后向算法,直接以盒子(隐)和球(观测)的实例为例推导:
(1)初始化第三次取球为红球时候,即最终时刻所有状态的概率为1
式中下标为观测情况,括号为隐状态,比如第一个式子意思就是第一个隐状态对应的观测到红球的概率
(2)逆推迭代倒数第二次观察情况为白球的情况
第一个式子表示的是第二次观测,如果状态为1,那么第二、三次观测为(白、红)的联合概率分布,a是第二层隐状态(第一个盒子)转移到第三层隐状态(三个盒子)的转移概率,b表示第三层的三个隐状态观测到红球的概率,β(等式右边)表示已知模型参数和第三层隐状态,求第三次观测到红球的概率,其实第(1)步计算是1
第二个式子表示的是第二次观测,如果状态为2,那么第二、三次观测为(白、红)的联合概率分布,a是第二层隐状态(第二个盒子)转移到第三层隐状态(三个盒子)的转移概率,b表示第三层的三个隐状态观测到红球的概率,β(等式右边)表示已知模型参数和第三层隐状态,求第三次观测到红球的概率,其实第(1)步计算是1
同理推导第一层的情况
(3)计算加和
可以发现前向算法和后向算法的结果相同
【注】前向算法中计算