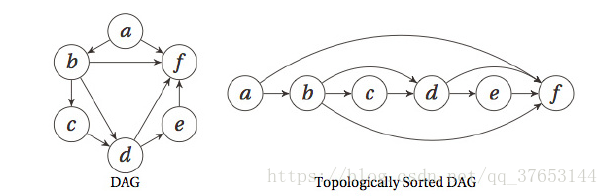
有向图及拓扑排序

有向图
在无向图中，边没有方向，两条边之间的顶点是单向可达的，而有向图的边是单向的。虽然边的性质不同，但我们仍然可以用邻接表来表示有向图。对有向图的结构定义如下：

#include <map>
#include <forward_list>
 
using namespace std;
 
struct DirectedGraph
{
    size_t V, E; //V表示顶点数，E表示边数
    map<int, forward_list<int>> adj; //邻接表
};

有向图在计算机中有广泛的应用，如任务调度条件、网络等。有向图的顶点之间的联系是描述现实世界的有利工具，如计算机的任务调度系统中，根据多任务之间的先后关联需要给出任务的执行顺序，拓扑排序就是可以得到这一顺序的算法。

拓扑排序
给定一幅有向图，将所有的顶点排序，使得所有的有向边均从排在前面的元素指向排在后面的元素（或者说明无法做到这一点）。

还是以任务调度系统为例，假设一个任务x必须在任务y之前完成，任务y必须在任务z之前完成，任务z又必须在任务x之前完成，这样的问题肯定是无解的。也就是说，拓扑排序能得出结果的前提是图必须是有向无环图（Directed Acyclic Graph，DAG），即一幅不含有环路的有向图。

一种拓扑排序的思想是基于深度优先搜索的顶点排序。它的基本思想是深度优先搜索会沿着开始顶点一直向下搜索，且正好只会访问每个顶点一次。基于深度优先搜索的拓扑排序基于一个重要命题：一幅有向图的拓扑顺序即为所有顶点的逆后序排列。所谓逆后序遍历即在路径达到最大深度后再保存（打印）顶点，得到后序遍历，将其逆向输出即可。

下面是基于深度优先搜索来得到拓扑排序后的顶点顺序（默认无环，因此未给出判断是否存在有向环的代码）：

void dfs(DirectedGraph &g, vector<int> &visited, stack<int> &st, int v)
{
    visited[v] = 1;
    for (int &i : g.adj[v])
    {
        if (!visited[v])
        {
            dfs(g, visited, st, i);
        }
    }
    st.push(v);
}
 
void TopologicalSort(DirectedGraph &g, int v)
{
    stack<int> st;
    vector<int> visited(g.V);
    dfs(g, visited, st, v);
    while (!st.empty())
    {
        cout << st.top() << " ";
        st.pop();
    }
}

另一种思路是得到所有顶点的入度，循环执行以下两个步骤直到不存在入度为0的顶点：

（1）选择一个入度为0的顶点，输出

（2）将该顶点其出边全部删除，同时更新出边所到达顶点的入度

这种算法不需要太多代码判断是否存在有向环，只要最后输出的顶点数小于有向图的顶点数就说明了存在有向环。

bool TopologicalSort(DirectedGraph &g, vector<int> &in_degree)
{
    queue<int> qu;
    int cnt = 0;
    for (auto ite = in_degree.begin(); ite != end(); ++ite)
    {
        if (0 == *ite)
        {
            qu.push(*ite);
        }
    }
    while (!qu.empty())
    {
        int v = qu.front();
        qu.pop();
        cout << v << " ";
        ++cnt;
        for (const int &i : g.adj.at(v))
        {
            if (0 == --in_degree[i])
            {
                qu.push(i);
            }
        }
    }
    if (cnt < V)
    {
        return false;
    }
    return true;
}