BitMap算法及其在lucene中的应用

bitmap应用场景

有一个无序有界int数组{1,2,5,7},初步估计占用内存44=16字节，这倒是没什么奇怪的；但是假如有10亿个这样的数呢，10亿4/(102410241024)=3.72G左右。如果这样的一个大的数据做查找和排序，那估计内存也崩溃了，有人说，这些数据可以不用一次性加载，那就是要存盘了，存盘必然消耗IO。

如果用BitMap思想来解决的话，就好很多。一个byte是占8个bit，如果每一个bit的值就是有或者没有，也就是二进制的0或者1，如果用bit的位置代表数组值有还是没有，那么0代表该数值没有出现过，1代表该数组值出现过。也可以描述数据。具体如下图：

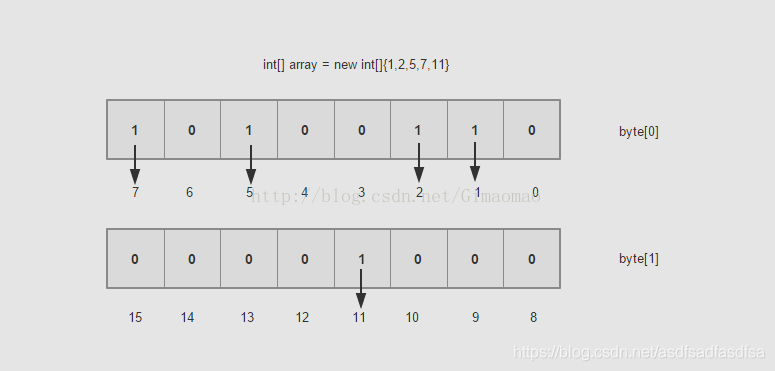
现在假如10亿的数据所需的空间就是3.72G/32，一个占用32bit的数据现在只占用了1bit，节省了不少的空间，排序就更不用说了，一切显得那么顺利。这样的数据之间没有关联性，要是读取的，你可以用多线程的方式去读取。时间复杂度方面也是O(Max/n)，其中Max为byte[]数组的大小，n为线程大小

算法实现

第一步： 构建特定长度的byte数组（new byte[capacity / 8 + 1]），其中 capacity为整数数组长度（如：10亿个数字、40亿个数字等）；

byte[] bits = new byte[getIndex(n) + 1];

第二步 ： 计算数字num在byte[]中的位置（num/8）；   

/**
     * num/8得到byte[]的index
     * @param num
     * @return
     */
    public int getIndex(int num){
        return num >> 3;
    }

第三步： 计算数字num在byte[index]的位置（num%8）；

 /**
     * num%8得到在byte[index]的位置
     * @param num
     * @return
     */
    public int getPosition(int num){
        return num & 0x07;
    }

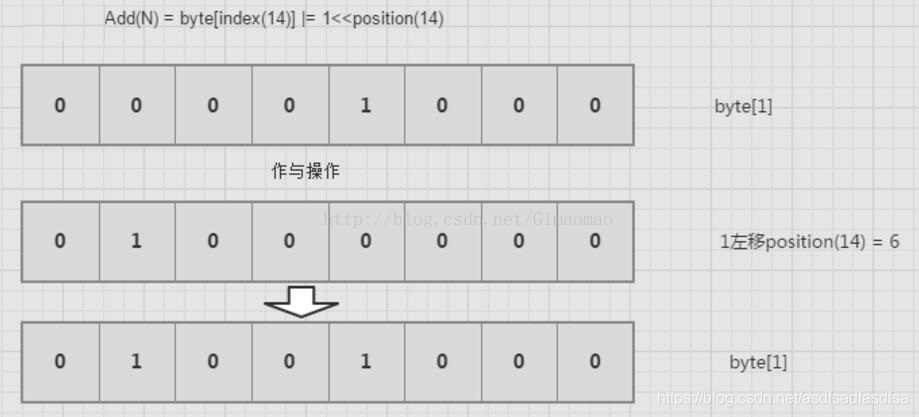
第四步： 将所在的位置从0变成1.其他位置不变；

 /**
     * 标记指定数字（num）在bitmap中的值，标记其已经出现过<br/>
     * 将1左移position后，那个位置自然就是1，然后和以前的数据做|，这样，那个位置就替换成1了
     * @param bits
     * @param num
     */
    public void add(byte[] bits, int num){
        bits[getIndex(num)] |= 1 << getPosition(num);
    }

第五步： 判断指定数字num是否已存在；

 /**
     * 判断指定数字num是否存在<br/>
     * 将1左移position后，那个位置自然就是1，然后和以前的数据做&，判断是否为0即可
     * @param bits
     * @param num
     * @return
     */
    public boolean contains(byte[] bits, int num){
        return (bits[getIndex(num)] & 1 << getPosition(num)) != 0;
    }

第六步：重置某一数字对应在bitmap中的值；

 /**
     * 重置某一数字对应在bitmap中的值<br/>
     * 对1进行左移，然后取反，最后与byte[index]作与操作。
     * @param bits
     * @param num
     */
    public void clear(byte[] bits, int num){
        bits[getIndex(num)] &= ~(1 << getPosition(num));
    }

 

算法在lucene合并倒排表中(多should查询求并集)的应用

public void collect(int doc) throws IOException {
      hasMatches = true;
        //doc为文档号， MASK的值为2047，作为理解倒排表合并的原理，我们不用考虑文档号大于2047的情况, 如果大于2047也不会被抛弃,而是重复利用?
      final int i = doc & MASK;
        // 每32篇文档都会记录在matching[idx]数组的同一个元素中
        // 比如说 0~31的文档号就被记录在 matching[0]这个数组元素中
      final int idx = i >>> 6;
        // 用来去重的存储文档号, 二进制表示的数值中，每个为1的bit位的所属第几位就是文档号的值
        // 比如 00...01001(32位二进制), 说明存储了 文档号 0跟3
        // matching在后面遍历中使用，因为我们还要判断每一篇文档出现的次数是否满足minSHouldMatch
        // 那么通过这个matching值就可以从buckets[]数组中以O(1)的复杂度找到每一篇文档出现的次数
      matching[idx] |= 1L << i;
        // 引用bucket对象，buckets[]数组下标是文档号
        // bucket中的freq统计某个文档号出现的次数
        // 这里的buckets是一个已经初始化了2048个大小的bucket数组
      final Bucket bucket = buckets[i];
      bucket.freq++;
      //这里的scorer是TermScorer类型
      //这里可以看出，打分是一个累加的过程
      bucket.score += scorer.score();
    }