概率图(三)--最大熵马尔科夫模型

最大熵模型

最大熵模型属于log-linear model，在给定训练数据的条件下对模型进行极大似然估计或正则化极大似然估计：

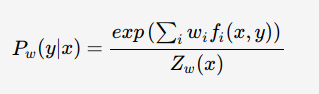
其中，为归一化因子，w为最大熵模型的参数，fi(x,y)为特征函数——描述(x,y)的某一事实

具体推导参见: https://blog.csdn.net/asdfsadfasdfsa/article/details/80833781

最大熵马尔科夫模型

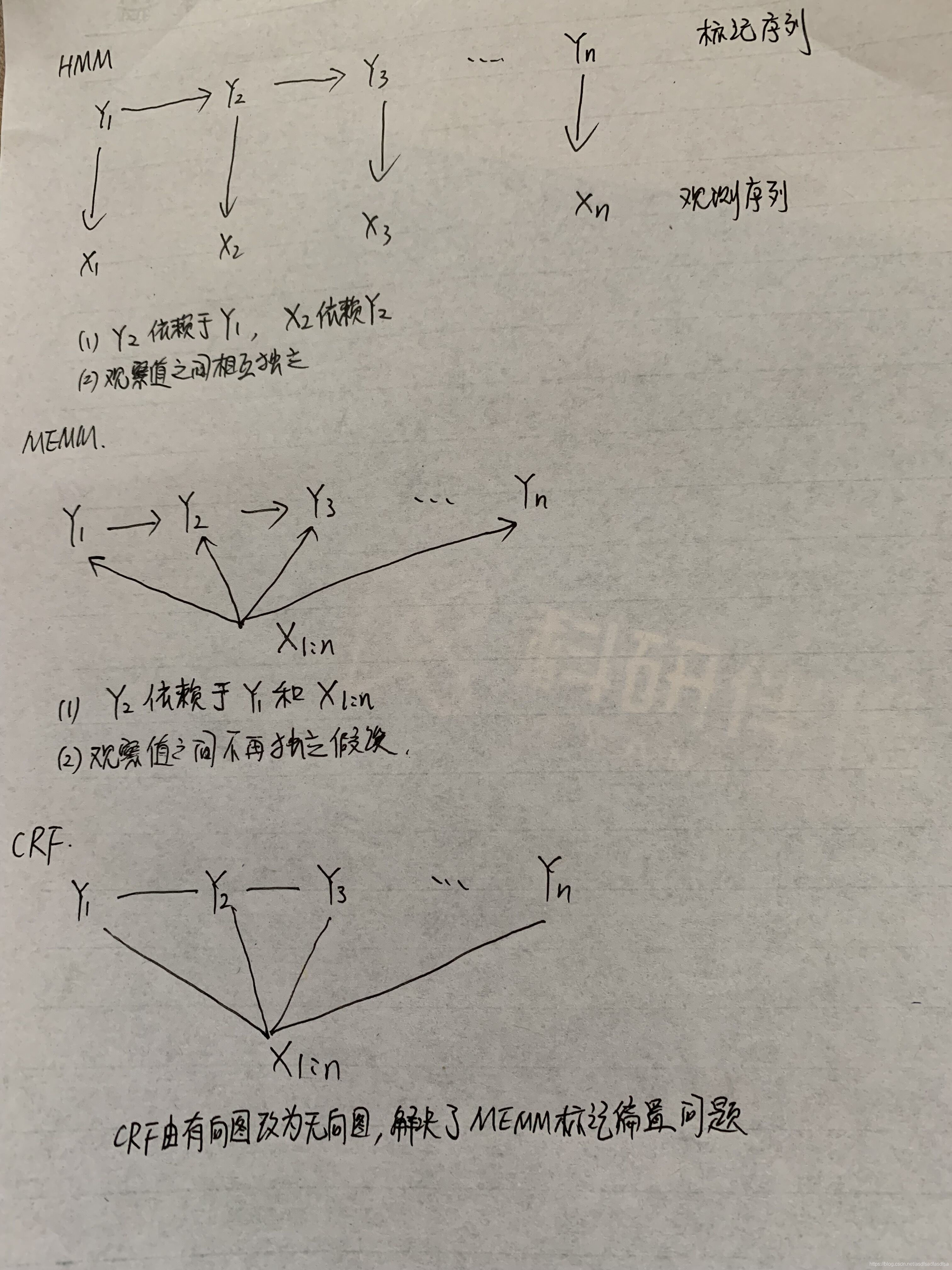
HMM模型中存在两个假设：一是输出观察值之间严格独立，二是状态的转移过程中当前状态只与前一状态有关。但实际上序列标注问题不仅和单个词相关，而且和观察序列的长度，单词的上下文，等等相关。MEMM解决了HMM输出独立性假设的问题。因为HMM只限定在了观测与状态之间的依赖，而MEMM引入自定义特征函数，不仅可以表达观测之间的依赖，还可表示当前观测与前后多个状态之间的复杂依赖。
这里由于去掉了独立性假设，所以不能给出联合概率分布，只能求后验概率，所以是判别模型

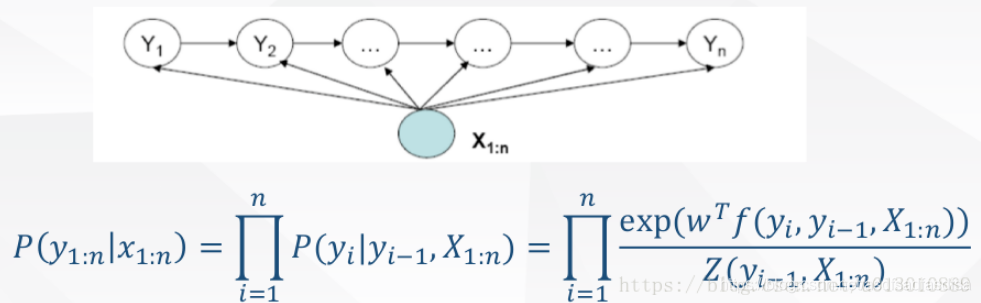
HMM中，观测节点 $o_{i}$ 依赖隐藏状态节点 $i_{i}$ ,也就意味着我的观测节点只依赖当前时刻的隐藏状态。但在更多的实际场景下，观测序列是需要很多的特征来刻画的，比如说，我在做NER时，我的标注 $i_{i}$ 不仅跟当前状态 $o_{i}$ 相关，而且还跟前后标注 $o_{j}(j \neq i)$ 相关，比如字母大小写、词性等等。

为此，提出来的MEMM模型就是能够直接允许“定义特征”，直接学习条件概率，即 $P(i_{i}|i_{i-1},o_{i}) (i = 1,\cdots,n)$ , 总体为：

$P(I|O) = \prod_{t=1}^{n}P(i_{i}|i_{i-1},o_{i}), i = 1,\cdots,n$

并且， $P(i|i^{'},o)$ 这个概率通过最大熵分类器建模（取名MEMM的原因）

$P(i|i^{'},o) = \frac{1}{Z(o,i^{'})} exp(\sum_{a})\lambda_{a}f_{a}(o,i)$

重点来了，这是ME的内容，也是理解MEMM的关键： $Z(o,i^{'})$ 这部分是归一化； $f_{a}(o,i)$ 是特征函数，具体点，这个函数是需要去定义的; $λ$ 是特征函数的权重，这是个未知参数，需要从训练阶段学习而得。

比如我可以这么定义特征函数：

$\begin{equation} f_{a}(o,i) = \begin{cases} 1& \text{满足特定条件}，\\ 0& \text{other} \end{cases} \end{equation}$

其中，特征函数 $f_{a}(o,i)$ 个数可任意制定， $（a = 1, \cdots, n）$

所以总体上，MEMM的建模公式这样：

$P(I|O) = \prod_{t=1}^{n}\frac{ exp(\sum_{a})\lambda_{a}f_{a}(o,i) }{Z(o,i_{i-1})} , i = 1,\cdots,n$

是的，公式这部分之所以长成这样，是由ME模型决定的。(最大熵模型中的权重lamba来自于拉格朗日因子)

请务必注意，理解判别模型和定义特征两部分含义，这已经涉及到CRF的雏形了

MEMM需要两点注意：

与HMM的 $o_{i}$ 依赖 $i_{i}$ 不一样，MEMM当前隐藏状态 $i_{i}$ 应该是依赖当前时刻的观测节点 $o_{i}$ 和上一时刻的隐藏节点 $i_{i-1}$
需要注意，之所以图的箭头这么画，是由MEMM的公式决定的，而公式是creator定义出来的???

最大熵马尔科夫模型标记偏置问题

MEMM讨论的最多的是他的labeling bias 问题。

1. 现象

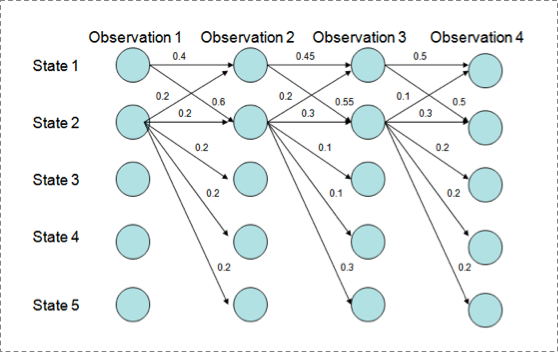
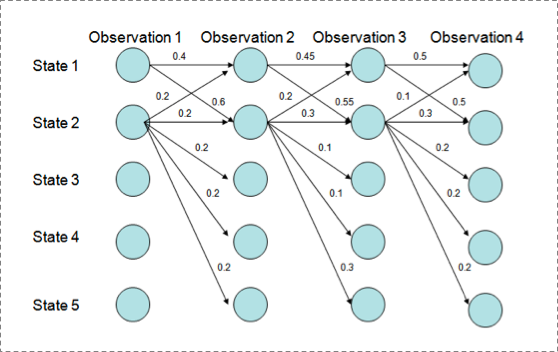
用Viterbi算法解码MEMM，状态1倾向于转换到状态2，同时状态2倾向于保留在状态2。解码过程细节（需要会viterbi算法这个前提）：

P(1-> 1-> 1-> 1)= 0.4 x 0.45 x 0.5 = 0.09 ，
P(2->2->2->2)= 0.2 X 0.3 X 0.3 = 0.018，
P(1->2->1->2)= 0.6 X 0.2 X 0.5 = 0.06，
P(1->1->2->2)= 0.4 X 0.55 X 0.3 = 0.066

但是得到的最优的状态转换路径是1->1->1->1，为什么呢？因为状态2可以转换的状态比状态1要多，从而使转移概率降低,即MEMM倾向于选择拥有更少转移的状态。

2. 解释原因

直接看MEMM公式：

$P(I|O) = \prod_{t=1}^{n}\frac{ exp(\sum_{a})\lambda_{a}f_{a}(o,i) }{Z(o,i_{i-1})} , i = 1,\cdots,n$

$∑$ 求和的作用在概率中是归一化，但是这里归一化放在了指数内部，管这叫local归一化。来了，viterbi求解过程，是用dp的状态转移公式（MEMM的没展开，请参考CRF下面的公式），因为是局部归一化，所以MEMM的viterbi的转移公式的第二部分出现了问题，导致dp无法正确的递归到全局的最优。

$\delta_{i+1} = max_{1 \le j \le m}\lbrace \delta_{i}(I) + \sum_{i}^{T}\sum_{k}^{M}\lambda_{k}f_{k}(O,I_{i-1},I_{i},i) \rbrace$

HMM->MEMM->CRF

MEMM解决了HMM输出独立性假设的问题。因为HMM只限定在了观测与状态之间的依赖，而MEMM引入自定义特征函数，以表达 P(当前标记|前一标记, 整个观测序列), 而HMM则是P(当前标记|前一标记, 当前观测值), 实际上HMM是当前标记依赖前一标记, 当前观测值依赖当前标记

而CRF将MEMM有向图改为无向图, 解决了MEMM标记偏置的问题

三者的共同特征是: 都基于马尔科夫假设, 即当前标记依赖前一标记

posted @ 2019-06-14 13:35 車輪の唄阅读(37) 评论(0) 编辑收藏举报来源

刷新页面返回顶部

車輪の唄

概率图(三)--最大熵马尔科夫模型

公告