cnn全连接层
1. 定义
全连接层(fully connected layers,FC)在整个卷积神经网络中起到“分类器”的作用。如果说卷积层、池化层和激活函数层等操作是将原始数据映射到隐层特征空间的话,全连接层则起到将学到的“分布式特征表示”映射到样本标记空间的作用。在实际使用中,全连接层可由卷积操作实现:对前层是全连接的全连接层可以转化为卷积核为1x1的卷积;而前层是卷积层的全连接层可以转化为卷积核为hxw的全局卷积,h和w分别为前层卷积结果的高和宽。
全连接的核心操作就是矩阵向量乘积
y = Wx
本质就是由一个特征空间线性变换到另一个特征空间。目标空间的任一维——也就是隐层的一个 cell——都认为会受到源空间的每一维的影响。不考虑严谨,可以说,目标向量是源向量的加权和。
在 CNN 中,全连接常出现在最后几层,用于对前面设计的特征做加权和。比如 mnist,前面的卷积和池化相当于做特征工程,后面的全连接相当于做特征加权。(卷积相当于全连接的有意弱化,按照局部视野的启发,把局部之外的弱影响直接抹为零影响;还做了一点强制,不同的局部所使用的参数居然一致。弱化使参数变少,节省计算量,又专攻局部不贪多求全;强制进一步减少参数。少即是多) 在 RNN 中,全连接用来把 embedding 空间拉到隐层空间,把隐层空间转回 label 空间等。
2. CNN与全连接
在CNN结构中,经多个卷积层和池化层后,连接着1个或1个以上的全连接层.与MLP类似,全连接层中的每个神经元与其前一层的所有神经元进行全连接.全连接层可以整合卷积层或者池化层中具有类别区分性的局部信息.为了提升 CNN网络性能,全连接层每个神经元的激励函数一般采用ReLU函数。最后一层全连接层的输出值被传递给一个输出,可以采用softmax逻辑回归(softmax regression)进行 分 类,该层也可 称为 softmax层(softmax layer).对于一个具体的分类任务,选择一个合适的损失函数是十分重要的,CNN几种常用的损失函数并分析了它们各自的特点.通 常,CNN的全连接层与MLP 结构一样,CNN的训练算法也多采用BP算法
举个例子:
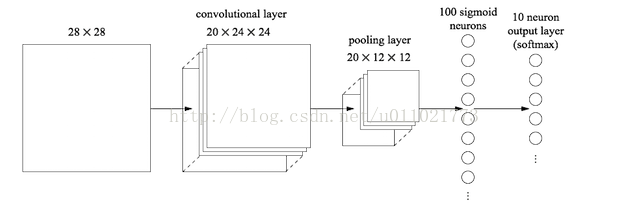
最后的两列小圆球就是两个全连接层,在最后一层卷积结束后,进行了最后一次池化,输出了20个12*12的图像,然后通过了一个全连接层变成了1*100的向量。
这是怎么做到的呢,其实就是有20*100个12*12的卷积核卷积出来的,对于输入的每一张图,用了一个和图像一样大小的核卷积,这样整幅图就变成了一个数了,如果厚度是20就是那20个核卷积完了之后相加求和。这样就能把一张图高度浓缩成一个数了。全连接的目的是什么呢?因为传统的网络我们的输出都是分类,也就是几个类别的概率甚至就是一个数--类别号,那么全连接层就是高度提纯的特征了,方便交给最后的分类器或者回归。
但是全连接的参数实在是太多了,你想这张图里就有20*12*12*100个参数,前面随便一层卷积,假设卷积核是7*7的,厚度是64,那也才7*7*64,所以现在的趋势是尽量避免全连接,目前主流的一个方法是全局平均值。
也就是最后那一层的feature map(最后一层卷积的输出结果),直接求平均值。有多少种分类就训练多少层,这十个数字就是对应的概率或者叫置信度。
卷积操作的意义:
卷积神经网络有两种神器可以降低参数数目,第一种神器叫做局部感知野。一般认为人对外界的认知是从局部到全局的,而图像的空间联系也是局部的像素联系较为紧密,而距离较远的像素相关性则较弱。因而,每个神经元其实没有必要对全局图像进行感知,只需要对局部进行感知,然后在更高层将局部的信息综合起来就得到了全局的信息。网络部分连通的思想,也是受启发于生物学里面的视觉系统结构。视觉皮层的神经元就是局部接受信息的(即这些神经元只响应某些特定区域的刺激)。
卷积即: 输出=输入*系统
卷积层的主要优点是参数共享和稀疏连接,这使得卷积操作所需要学习的参数数量大大减少
https://blog.csdn.net/weixin_42451919/article/details/81381294