RSA-ctf-小总结——不定时更新

最近做了很多关于rsa的题，来小结一下~

以下只介绍常用方法，不介绍相关原理，小伙伴们可以自行百度，或者观看斯坦福的密码学课程（b站有中字）~

首先几个最常用的公式：

φ(n) = (p-1)(q-1)

ed ≡ 1 (mod φ(n))

e,n都是公开的，p和q是非公开。

公钥：（n,e）

密钥：  (n,d)

加密：c≡ m^e mod n

解密：m≡ c^d mod n

情况一：n已知，可通过工具爆破出p,q。例如使用在线拆分，或者利用yafu（github有相关教程），其中yafu在使用时用cmd命令打开，单独运行yafu爆破出来的时候会直接闪退。

 

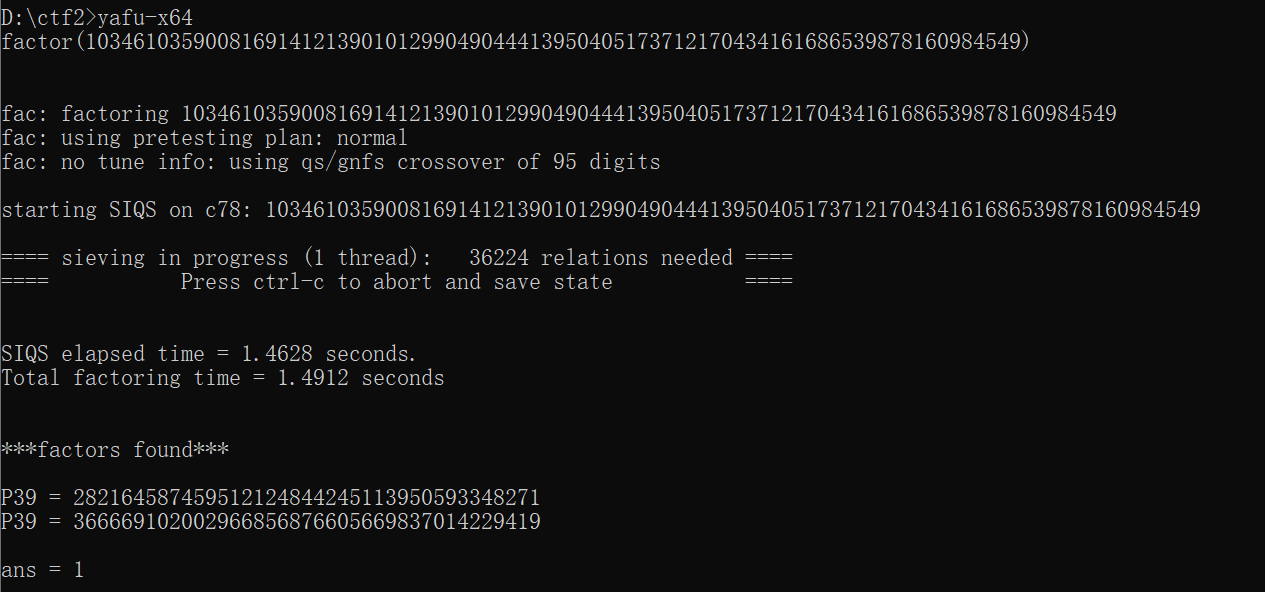
 情况二：已知n,c,m，如果e的值不大，可以通过c≡ m^e mod n，在一定范围内，爆破出e。

 

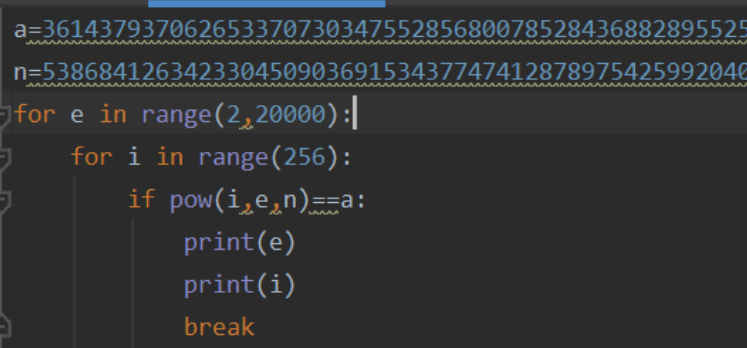
情况三：利用工具，例如rsatool,RsaCtfTool，oppensl,在解pem文件的时候，利用上述工具，由于楼主在kail中使用rsatool生成pem文件时，报错psanl1框架错误，至今没有找到解决方法，待解决后，再来更新此文章。

情况四：维纳攻击，特征：e特别大

from RSAwienerHacker import hack_RSA 
import libnum 
e=46867417013414476511855705167486515292101865210840925173161828985833867821644239088991107524584028941183216735115986313719966458608881689802377181633111389920813814350964315420422257050287517851213109465823444767895817372377616723406116946259672358254060231210263961445286931270444042869857616609048537240249 
n=86966590627372918010571457840724456774194080910694231109811773050866217415975647358784246153710824794652840306389428729923771431340699346354646708396564203957270393882105042714920060055401541794748437242707186192941546185666953574082803056612193004258064074902605834799171191314001030749992715155125694272289 
d=hack_RSA(e,n) 
enc=37625098109081701774571613785279343908814425141123915351527903477451570893536663171806089364574293449414561630485312247061686191366669404389142347972565020570877175992098033759403318443705791866939363061966538210758611679849037990315161035649389943256526167843576617469134413191950908582922902210791377220066 
m=pow(enc ,d ,n) 
print libnum.n2s(m)

情况五：啥都已知解明文

import libnum
from Crypto.Util.number import long_to_bytes
q = int(
    "0xa6055ec186de51800ddd6fcbf0192384ff42d707a55f57af4fcfb0d1dc7bd97055e8275cd4b78ec63c5d592f567c66393a061324aa2e6a8d8fc2a910cbee1ed9",
    16)
p = int(
    "0xfa0f9463ea0a93b929c099320d31c277e0b0dbc65b189ed76124f5a1218f5d91fd0102a4c8de11f28be5e4d0ae91ab319f4537e97ed74bc663e972a4a9119307",
    16)
e = int(
    "0x6d1fdab4ce3217b3fc32c9ed480a31d067fd57d93a9ab52b472dc393ab7852fbcb11abbebfd6aaae8032db1316dc22d3f7c3d631e24df13ef23d3b381a1c3e04abcc745d402ee3a031ac2718fae63b240837b4f657f29ca4702da9af22a3a019d68904a969ddb01bcf941df70af042f4fae5cbeb9c2151b324f387e525094c41",
    16)
c = 0x7fe1a4f743675d1987d25d38111fae0f78bbea6852cba5beda47db76d119a3efe24cb04b9449f53becd43b0b46e269826a983f832abb53b7a7e24a43ad15378344ed5c20f51e268186d24c76050c1e73647523bd5f91d9b6ad3e86bbf9126588b1dee21e6997372e36c3e74284734748891829665086e0dc523ed23c386bb520
n = q * p
d = libnum.invmod(e, (p - 1) * (q - 1))
m = pow(c, d, n)  # m 的十进制形式
string = long_to_bytes(m)  # m明文
print(string)  # 结果为 b‘ m ’ 的形式