【带你装逼带你飞】吐血总结了这五大常用算法技巧,让你在同事/面试官面前惊艳全场!
对于算法技巧,之前的文章也写过一些算法技巧,不过相对零散一些,今天我把之前的很多文章总结了下,并且通过增删查改,给大家总结一些常用的算法解题技巧,当然,这些也不是多牛逼的技巧,不过可以让你的代码看起来更加短小精悍,如果你能够充分掌握这些技巧,能够混合运用起来,那么写出来的代码,必然可以让别人拍案叫绝。
1、多思考能否使用位运算
如果你去看一些大佬的解题代码,你会发现大部分代码里都会出现位运算相关的代码,而且不瞒你说,如果我看到一个人的代码里,如果出现了位运算,我就会感觉这个人还是有点东西。
最简单地位运算使用场景就是当我们在进行除法和乘法运算的时候了,例如每次遇到 n / 2,n / 4,n / 8这些运算地时候,完全可以使用位运算,也可以使你地代码运行效率更高,例如
n / 2 等价于 n >> 1
n / 4 等价于 n >> 2
n / 8 等价于 n >> 3。
当然,如果你现在去找个 IDE 写个代码测试下 n / 2 和 n >> 1 的运行效率,可能会发现没啥差别,其实并非没有差别,而是大部分编译器会自动帮你把 n / 2 优化成 n >> 1,不过我还是建议你写成 n >> 1,这可以让你的代码显的更加牛逼一些,给面试官的印象可能也会好一些。当然,我说的说可能。
还有一个非常常用的就是奇偶的判断,判断一个数是否说奇数,常规操作长这样
if( n % 2 == 1){
dosomething();
}
不过你可以采用与运算来代替 n % 2,改成这样
if( (n & 2) == 1){
dosomething();
}
你去看源码的话,基本都是采用这些位运算的,如果你用惯,以后遇到这些代码,看起来也会比较容易懂。
上面列举的这个说最常用的,也说不上什么技巧,不过建议可以多使用熟悉,对于位运算的技巧,我推荐你熟悉如下几个。
1、利用 n & (n - 1)消去 n 最后的一位 1
在 n 的二进制表示中,如果我们对 n 执行
n = n & (n - 1)
那么可以把 n 最右边的 1 消除掉,例如
n = 1001
n - 1 = 1000
n = n & (n - 1) = (1001) & (1000) = 1000
这个公式有哪些用处呢?
其实还是有挺多用处的,在做题的时候也是会经常碰到,下面我列举几道经典、常考的例题。
(1)、判断一个正整数 n 是否为 2 的幂次方
如果一个数是 2 的幂次方,意味着 n 的二进制表示中,只有一个位 是1,其他都是0。我举个例子,例如
2^0 = 0…..0001
2^1 = 0…..0010
2^2 = 0….0100
那么我们完全可以对 n 执行 n = n & (n - 1),执行之后结果如果不为 0,则代表 n 不是 2 的幂次方,代码如下
boolean judege(int n){
return (n & (n - 1)) == 0;//
}
如果你使用常规手段对话,得把 n 不停着除以 2,最后判断得出结果,用这个位运算技巧,一行代码搞定。
(2)、判断 正整数 n 的二进制表示中有多少个 1
例如 n = 13,那么二进制表示为 n = 1101,那么就表示有 3 个1,这道题常规做法还是把 n 不停着除以 2,然后统计除后的结果是否为奇数,是则 1 的个数加 1,否则不需要加1,继续除以 2。
不过对于这种题,我们可以用不断着执行 n & (n - 1),每执行一次就可以消去一个 1,当 n 为 0 时,计算总共执行了多少次即可,代码如下:
public int NumberOf12(int n) {
int count = 0;
int k = 1;
while (n != 0) {
count++;
n = (n - 1) & n;
}
return count;
代码不仅更加短小精悍,而且效率更高,关于 n & (n - 1),我就暂时举例这两个,主要是后面还有非常多的技巧要写。
2、异或(^)运算的妙用
关于异或运算符,我们先来看下他的特性
特性一:两个相同的数相互异或,运算结果为 0,例如 n ^ n = 0;
特性二:任何数和 0 异或,运算结果不变,例如 n ^ 0 = n;
特性三:支持交换律和结合律,例如 x ^ ( y ^ x) = (x ^ y) ^ x;
案例1:只出现一次是数
问题:数组中,只有一个数出现一次,剩下都出现两次,找出出现一次的数
常规操作就是一边遍历数组一边用哈希表统计元素出现的次数数,最后再遍历哈希表,看看哪个数只出现了一次。这种方法的时间复杂度为 O(n),空间复杂度也为 O(n)了。
我们刚才说过,两个相同的数异或的结果是 0,一个数和 0 异或的结果是它本身,所以我们把这一组整型全部异或一下,例如这组数据是:1, 2, 3, 4, 5, 1, 2, 3, 4。其中 5 只出现了一次,其他都出现了两次,把他们全部异或一下,结果如下:
由于异或支持交换律和结合律,所以:
123451234 = (11)(22)(33)(44)5= 00005 = 5。
通过这种方法,可以把空间复杂度降低到 O(1),而时间复杂度不变,相应的代码如下
int find(int[] arr){
int tmp = arr[0];
for(int i = 1;i < arr.length; i++){
tmp = tmp ^ arr[i];
}
return tmp;
}
关于位运算的技巧真的挺多,不过由于篇幅原因,我就暂时先举例这么多,重点的要告诉你,平时在刷题的时候,多留意下这些技巧,然后可以总结下来,之后自己遇到的时候可以应用上去。
2、考虑是否可以使用数组下标
数组的下标是一个隐含的很有用的数组,特别是在统计一些数字,或者判断一些整型数是否出现过的时候。例如,给你一串字母,让你判断这些字母出现的次数时,我们就可以把这些字母作为下标,在遍历的时候,如果字母a遍历到,则arr[a]就可以加1了,即 arr[a]++;
通过这种巧用下标的方法,我们不需要逐个字母去判断。
我再举个例子:
问题:给你n个无序的int整型数组arr,并且这些整数的取值范围都在0-20之间,要你在 O(n) 的时间复杂度中把这 n 个数按照从小到大的顺序打印出来。
对于这道题,如果你是先把这 n 个数先排序,再打印,是不可能O(n)的时间打印出来的。但是数值范围在 0-20。我们就可以巧用数组下标了。把对应的数值作为数组下标,如果这个数出现过,则对应的数组加1。
public void f(int arr[]) {
int[] temp = new int[21];
for (int i = 0; i < arr.length; i++) {
temp[arr[i]]++;
}
//顺序打印
for (int i = 0; i < 21; i++) {
for (int j = 0; j < temp[i]; j++) {
System.out.println(i);
}
}
}
我在举一个例子
假如给你20亿个非负数的int型整数,然后再给你一个非负数的int型整数 t ,让你判断t是否存在于这20亿数中,你会怎么做呢?
有人可能会用一个int数组,然后把20亿个数给存进去,然后再循环遍历一下就可以了。
想一下,这样的话,时间复杂度是O(n),所需要的内存空间
4byte * 20亿,一共需要80亿个字节
如果采用下标法,我们可以把时间复杂度降低位 O(1),例如我们可以这样来存数据,把一个 int 非负整数 n 作为数组下标,如果 n 存在,则对应的值为1,如果不存在,对应的值为0。例如数组arr[n] = 1,表示n存在,arr[n] = 0表示n不存在。
那么,我们就可以把20亿个数作为下标来存,之后直接判断arr[t]的值,如果arr[t] = 1,则代表存在,如果arr[t] = 0,则代表不存在。这样,我们就可以把时间复杂度降低到O(1)。
那么大家想一下,空间上可以继续优化吗?
答是可以的,因为如果不需要统计个数,我们我们不需要 int 数组,用boolean类型的数组他不香吗?boolean类型占用的空间更少。
那么大家想一下,还能继续优化吗?
答是可以的,可以用 bitmap 算法,具体我这里不展开,感兴趣看这篇文章:【面试现场】如何判断一个数是否在40亿个整数中?
关于下标法的,在做题的时候,真的用到提多,这里推荐大家以后做题的时候可以关注一下,我就暂时先讲这么多。
3、考虑能否使用双指针
双指针这个技巧,那就更加常用的,特别是在链表和有序数组中,例如
给定一个整数有序数组和一个目标值,找出数组中和为目标值的两个数,并且打印出来
一种简单的做法就是弄个两层的 for 循环,然而对于这种有序的数组,如果是要寻找某个数之类的,大概率可以考虑双指针,也就是设置一个头指针和尾指针,直接看代码吧,代码如下:
int find(int arr[], int target){
int left = 0;//头指针
int right = arr.length - 1;// 尾指针
while(left < right){
if(left + right == target){
// 找到目标数,进行打印,这里我就不执行打印操作两
}else if(left + right < target){
left ++;
}else{
right --;
}
}
}
在 leetcode 中的三数之和和四数只和都可以采用这个类型的双指针来处理。
当然,双指针在链表中也是非常给力的,例如
在做关于单链表的题是特别有用,比如“判断单链表是否有环”、“如何一次遍历就找到链表中间位置节点”、“单链表中倒数第 k 个节点”等问题。对于这种问题,我们就可以使用双指针了,会方便很多。我顺便说下这三个问题怎么用双指针解决吧。
例如对于第一个问题
我们就可以设置一个慢指针和一个快指针来遍历这个链表。慢指针一次移动一个节点,而快指针一次移动两个节点,如果该链表没有环,则快指针会先遍历完这个表,如果有环,则快指针会在第二次遍历时和慢指针相遇。
对于第二个问题
一样是设置一个快指针和慢指针。慢的一次移动一个节点,而快的两个。在遍历链表的时候,当快指针遍历完成时,慢指针刚好达到中点。
对于第三个问题
设置两个指针,其中一个指针先移动k个节点。之后两个指针以相同速度移动。当那个先移动的指针遍历完成的时候,第二个指针正好处于倒数第k个节点。
你看,采用双指针方便多了吧。所以以后在处理与链表相关的一些问题的时候,可以考虑双指针哦。
关于双指针,在这里也是给大家提个醒,重要的还是要大家多考虑,以后才能顺手拈来。
4、从递归到备忘录到递推或者动态规划
递归真的太好用了,好多问题都可以使用递归来解决,不过 80% 的递归提都可以进行剪枝,并且还有还多带有备忘录的递归都可以转化为动态规划,我本来是要举例一个二维DP的动态规划题,较大家从递归 =》递归+备忘录 =》动态规划 =》动态规划优化的。
不过写起来有点多,并且有一定的难度,感觉有点偏离来这篇文章所有的技巧总结,所以我还来列举一个简单的例子吧,这个例子重在告诉大家遇到递归的题,一定要考虑是否可以剪枝,是否可以把递归转化成递推。
例如这个被我举烂的例子
(1).对于可以递归的问题务必考虑是否有重复计算的
当我们使用递归来解决一个问题的时候,容易产生重复去算同一个子问题,这个时候我们要考虑状态保存以防止重复计算。例如我随便举一个之前举过的问题
问题:一只青蛙一次可以跳上1级台阶,也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法?
这个问题用递归很好解决。假设 f(n) 表示n级台阶的总跳数法,则有
f(n) = f(n-1) + f(n - 2)。
递归的结束条件是当0 <= n <= 2时, f(n) = n。因此我们可以很容易写出递归的代码
public int f(int n) {
if (n <= 2) {
return n;
} else {
return f(n - 1) + f(n - 2);
}
}
不过对于可以使用递归解决的问题,我们一定要考虑是否有很多重复计算,一种简单的方法就是大家可以画一个图来看下。如这道题
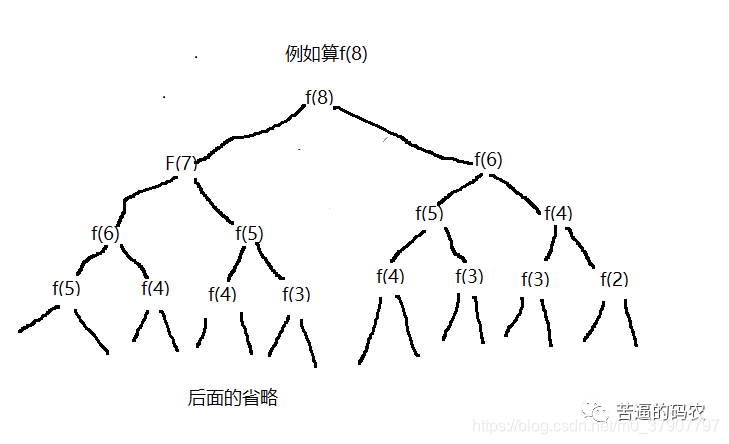
显然对于 f(n) = f(n-1) + f(n-2) 的递归,是有很多重复计算的。这个时候我们要考虑状态保存。例如用hashMap来进行保存,当然用一个数组也是可以的,这个时候就像我们上面说的巧用数组下标了。可以当arr[n] = 0时,表示n还没计算过,当arr[n] != 0时,表示f(n)已经计算过,这时就可以把计算过的值直接返回回去了。因此我们考虑用状态保存的做法代码如下:
//数组的大小根据具体情况来,由于int数组元素的的默认值是0
int[] arr = new int[1000];
public int f(int n) {
if (n <= 2) {
return n;
} else {
if (arr[n] != 0) {
return arr[n];//已经计算过,直接返回
} else {
arr[n] = f(n-1) + f(n-2);
return arr[n];
}
}
}
这样,可以极大着提高算法的效率。也有人把这种状态保存称之为备忘录法。
(2).考虑自底向上
对于递归的问题,我们一般都是从上往下递归的,直到递归到最底,再一层一层着把值返回。
不过,有时候当n比较大的时候,例如当 n = 10000时,那么必须要往下递归10000层直到 n <=2 才将结果慢慢返回,如果n太大的话,可能栈空间会不够用。
对于这种情况,其实我们是可以考虑自底向上的做法的。例如我知道
f(1) = 1;
f(2) = 2;
那么我们就可以推出 f(3) = f(2) + f(1) = 3。从而可以推出f(4),f(5)等直到f(n)。因此,我们可以考虑使用自底向上的方法来做。
代码如下:
public int f(int n) {
if(n <= 2)
return n;
int f1 = 1;
int f2 = 2;
int sum = 0;
for (int i = 3; i <= n; i++) {
sum = f1 + f2;
f1 = f2;
f2 = sum;
}
return sum;
}
我们也把这种自底向上的做法称之为递推。
根据这种带备忘录的递归,往往可以演变成动态规划,大家可以拿 leetcode 这两道题试试水
leetcode 的 62 号题:https://leetcode-cn.com/problems/unique-paths/
leetcode 的第64题:https://leetcode-cn.com/problems/minimum-path-sum/
总结一下
当你在使用递归解决问题的时候,要考虑以下两个问题
(1). 是否有状态重复计算的,可不可以使用备忘录法来优化。
(2). 是否可以采取递推的方法来自底向上做,减少一味递归的开销。
5、考虑是否可以设置哨兵位来处理临届问题
在链表的相关问题中,我们经常会设置一个头指针,而且这个头指针是不存任何有效数据的,只是为了操作方便,这个头指针我们就可以称之为哨兵位了。
例如我们要删除头第一个节点是时候,如果没有设置一个哨兵位,那么在操作上,它会与删除第二个节点的操作有所不同。但是我们设置了哨兵,那么删除第一个节点和删除第二个节点那么在操作上就一样了,不用做额外的判断。当然,插入节点的时候也一样。
有时候我们在操作数组的时候,也是可以设置一个哨兵的,把arr[0]作为哨兵。例如,要判断两个相邻的元素是否相等时,设置了哨兵就不怕越界等问题了,可以直接arr[i] == arr[i-1]?了。不用怕i = 0时出现越界。
当然我这只是举一个例子,具体的应用还有很多,例如插入排序,环形链表等。
总结
关于上面说的技巧,我只能说熟能生巧,居然要熟,首先你得要有机会接触到这样一算思想,而我上面的这些总结,便是给你找来机会接触这些思想,并且还都给出了例子,大家可以好好消化下,这篇文章的内容有些虽然是之前总结过的,不过这一次增加了一些新的东西和例子,还是花了不少时间,希望能够给大家带来一些帮助勒。
如果喜欢我的文章,欢迎各位关注我的公众号:帅地玩编程,专注于讲解算法,数据结果,计算机基础知识(计算机网络+ 操作系统+数据库+Linux),而这些都是每个程序员必修地底层内功,帅地带你装逼带你飞。
兄dei,如果觉得我写的不错,不妨帮个忙
1、关注我的原创微信公众号「帅地玩编程」,每天准时推送干货技术文章,专注于写算法 + 计算机基础知识(计算机网络+ 操作系统+数据库+Linux),听说关注了的不优秀也会变得优秀哦。
2、给俺点个赞呗,可以让更多的人看到这篇文章,顺便激励下我,嘻嘻。
作者简洁
作者:大家好,我是帅地,从大学、自学一路走来,深知算法,计算机基础知识的重要性,所以申请了一个微星公众号『帅地玩编程』,专业于写这些底层知识,提升我们的内功,帅地期待你的关注,和我一起学习。 转载说明:未获得授权,禁止转载



 浙公网安备 33010602011771号
浙公网安备 33010602011771号