一个简单的C4.5算法,采用Python语言
Test1.py 主要是用来运行的 代码如下:
# -*- coding: utf-8 -*- from math import log import operator import treePlotter def calcShannonEnt(dataSet): """ 输入:数据集 输出:数据集的香农熵 描述:计算给定数据集的香农熵;熵越大,数据集的混乱程度越大 """ # 数据集个数 numEntries = len(dataSet) #print("dd",numEntries) # 标签个数 labelCounts = {} for featVec in dataSet: # 获取每一行的结果 也就是yes or no currentLabel = featVec[-1] # print('e',currentLabel) # 判断我获取的这个yes or no 在不在labelCounts字典中 如果不在创建新的设置为0 if currentLabel not in labelCounts.keys(): labelCounts[currentLabel] = 0 labelCounts[currentLabel] += 1 #print('r',labelCounts) shannonEnt = 0.0 for key in labelCounts: # 计算类别信息熵 prob = float(labelCounts[key])/numEntries shannonEnt -= prob * log(prob, 2) #print('----',shannonEnt) return shannonEnt # 分别按照这几个属性来计算信息熵 找出最大的,最后按照这一个来划分。 def splitDataSet(dataSet, axis, value): """ 输入:数据集,选择维度,选择值 输出:划分数据集 描述:按照给定特征划分数据集;去除选择维度中等于选择值的项 """ retDataSet = [] # 这个时候 dataSet 还是完整的 for featVec in dataSet: # print(axis,featVec) # print('A',featVec[axis],"是不是等于",value) if featVec[axis] == value: reduceFeatVec = featVec[:axis] # print("B",reduceFeatVec,"此时的维度:",axis) reduceFeatVec.extend(featVec[axis+1:]) retDataSet.append(reduceFeatVec) # print('GG',retDataSet) return retDataSet def chooseBestFeatureToSplit(dataSet): """ 输入:数据集 输出:最好的划分维度 描述:选择最好的数据集划分维度 """ # 特征数量 也就是字段个数 numFeatures = len(dataSet[0]) - 1 ################################################################### # (1)信息增益 # print('cc',numFeatures) # 信息增益实际上是ID3算法中用来进行属性选择度量的。 # 它选择具有最高信息增益的属性来作为节点N的分裂属性。 # 该属性使结果划分中的元组分类所需信息量最小。 # 对D中的元组分类所需的期望信息为下式: baseEntropy = calcShannonEnt(dataSet) # 香农熵 # print('z',baseEntropy) bestInfoGainRatio = 0.0 # 最好的熵 bestFeature = -1 # 最好的特征 for i in range(numFeatures): featList = [example[i] for example in dataSet] uniqueVals = set(featList) # print('s',i,uniqueVals) newEntropy = 0.0 splitInfo = 0.0 for value in uniqueVals: # 划分数据集 # print("Bn",i,value) subDataSet = splitDataSet(dataSet, i, value) #print("After",subDataSet,i,value) prob = len(subDataSet)/float(len(dataSet)) # 现在假定按照属性A划分D中的元组,且属性A将D划分成v个不同的类。 # 在该划分之后,为了得到准确的分类还需要的信息由下面的式子度量 newEntropy += prob * calcShannonEnt(subDataSet) # 信息增益定义为原来的信息需求(即仅基于类比例)与新需求(即对A划分之后得到的)之间的差 splitInfo += -prob * log(prob, 2) # 信息增益 infoGain = baseEntropy - newEntropy ########################################################################## if (splitInfo == 0): # 修复溢出错误 continue ######################################################################### # (2)信息增益率 # 训练数据集D划分成对应于属性A测试的v个输出的v个划分产生的信息。信息增益率定义: infoGainRatio = infoGain / splitInfo # 选择具有最大增益率的属性作为分裂属性。 if (infoGainRatio > bestInfoGainRatio): bestInfoGainRatio = infoGainRatio bestFeature = i return bestFeature def majorityCnt(classList): """ 输入:分类类别列表 输出:子节点的分类 描述:数据集已经处理了所有属性,但是类标签依然不是唯一的, 采用少数服从多数的原则决定该子节点的分类 """ ''' 找出数量最多的分类 ''' # 分类字典 classCount = {} for vote in classList: if vote not in classCount.keys(): classCount[vote] = 0 classCount[vote] += 1 # 创建键值为classList中唯一值的数据字典,字典对象存储了classList中每个类标签出现的频率,最后利用operator操作键值排序字典,并返回出现次数最多的分类名称。 # iteritems:迭代器 # operator模块提供的itemgetter函数用于获取对象的哪些维的数据,参数为一些序号(即需要获取的数据在对象中的序号) # sorted() 是Python内置的一个排序函数,它会从一个"迭代器"返回一个排好序的新列表。 sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reversed=True) return sortedClassCount[0][0] # 创建决策树 参数:数据集、标签 def createTree(dataSet, labels): """ 输入:数据集,特征标签 输出:决策树 描述:递归构建决策树,利用上述的函数 """ # 截取dataSet的最后一行 classList = [example[-1] for example in dataSet] # 数据集都是同一类的情况 if classList.count(classList[0]) == len(classList): return classList[0] # 遍历完所有特征时返回出现次数最多的 #print('bb',dataSet[1]) # 如果数据集只有一个特征的情况 if len(dataSet[0]) == 1: return majorityCnt(classList) # 最大增益率的属性作为分裂属性 bestFeat = chooseBestFeatureToSplit(dataSet) # 最好的特征 # print('bestFeat',bestFeat) # 0 2 当选择0(outlook)之后 剩下的012中选择2(windy)中 bestFeatLabel = labels[bestFeat] # 最好的分类 myTree = {bestFeatLabel:{}} # print(myTree) # {'outlook': {}} {'windy': {}} del(labels[bestFeat]) # 得到列表包括节点所有的属性值 featValues = [example[bestFeat] for example in dataSet] # print('featValues',featValues) uniqueVals = set(featValues) # print('uniqueVals',uniqueVals) for value in uniqueVals: # 去掉前面标签之后剩下的标签 subLabels = labels[:] # print('subLabels',subLabels) myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), subLabels) # print('myTree',myTree) return myTree def classify(inputTree, featLabels, testVec): """ 输入:决策树,分类标签,测试数据 输出:决策结果 描述:跑决策树 """ firstStr = list(inputTree.keys())[0] # print('t2',firstStr) secondDict = inputTree[firstStr] #print('t3',secondDict) featIndex = featLabels.index(firstStr) # print('t4',featIndex) for key in secondDict.keys(): #print('key',key) if testVec[featIndex] == key: #print('testVec[featIndex]',testVec[featIndex]) if type(secondDict[key]).__name__ == 'dict': classLabel = classify(secondDict[key], featLabels, testVec) else: classLabel = secondDict[key] # print('t5',classLabel) return classLabel # 通过输入的决策树和对应的标签 来对测试集合 进行预测 def classifyAll(inputTree, featLabels, testDataSet): """ 输入:决策树,分类标签,测试数据集 输出:决策结果 描述:跑决策树 """ # 空列表 classLabelAll = [] for testVec in testDataSet: # print('t1',testVec) # 将预测结果插入到classLabelAll中 classLabelAll.append(classify(inputTree, featLabels, testVec)) # print("t6",classLabelAll) return classLabelAll # 训练集 def createDataSet(): """ 天气情况 outlook-> sunny | overcast | rain 温度情况 temperature-> hot | mild | cool 湿度情况 humidity-> high | normal 风力情况 windy-> false | true """ ######## no or yes is play golf ??? dataSet = [["sunny", "hot", "high", "false", 'no'], ["sunny", "hot", "high", "true", 'no'], ["overcast", "hot", "high", "false", 'yes'], ["rain", "mild", "high", "false", 'yes'], ["rain", "cool", "normal", "false", 'yes'], ["rain", "cool", "normal", "true", 'no'], ["overcast","cool", "normal", "true", 'no'], ["rain", "hot", "high", "true", 'yes'], ["sunny", "mild", "high", "true", 'no'], ["rain", "hot", "normal", "true", 'yes'], ["overcast","mild", "high", "false", 'no']] # 对应的标签 labels = ['outlook', 'temperature', 'humidity', 'windy'] return dataSet, labels # 测试集 def createTestSet(): testSet = [["sunny", "mild", "high", "false"], ["sunny", "cool", "normal", "false"], ["rain", "mild", "normal", "false"], ["sunny", "mild", "normal", "true"], ["overcast","mild", "high", "true"], ["rain", "hot", "normal", "true"], ["sunny", "mild", "normal", "false"], ["rain", "hot", "high", "true"], ["sunny", "mild", "high", "true"], ["rain", "hot", "normal", "true"], ["overcast", "mild", "high", "false"], ["rain", "mild", "high", "true"]] return testSet #主函数 定义 def main(): dataSet, labels = createDataSet() labels_tmp = labels[:] # 拷贝 labels Tree = createTree(dataSet, labels_tmp) print('Tree:\n', Tree) treePlotter.createPlot(Tree) print('------------------------------') # 获取测试集 进行预测 testSet = createTestSet() print('classifyResult:\n', classifyAll(Tree, labels, testSet)) # 调用主函数 if __name__ == '__main__': main()
treePlotter.py 用来画决策树。 代码如下所示:
import matplotlib.pyplot as plt # 定义文本框和箭头格式 decisionNode = dict(boxstyle="sawtooth", fc="0.8") leafNode = dict(boxstyle="round4", fc="0.8") arrow_args = dict(arrowstyle="<-") # 绘制带箭头的注释 def plotNode(nodeTxt, centerPt, parentPt, nodeType): createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction', \ xytext=centerPt, textcoords='axes fraction', \ va="center", ha="center", bbox=nodeType, arrowprops=arrow_args) ''' 获得决策树的叶节点数 ''' def getNumLeafs(myTree): numLeafs = 0 # fistStr获得字典的键 代表树根 firstStr = list(myTree.keys())[0] # 头结点 # print('firstStr',firstStr) secondDict = myTree[firstStr] # 取出头结点的的字典 for key in secondDict.keys(): # 测试节点的数据类型是否为字典 if type(secondDict[key]).__name__ == 'dict': numLeafs += getNumLeafs(secondDict[key]) else: numLeafs += 1 return numLeafs ''' 求树的深度 ''' def getTreeDepth(myTree): maxDepth = 0 firstStr = list(myTree.keys())[0] # 头结点 secondDict = myTree[firstStr] for key in secondDict.keys(): # 测试节点的数据类型是否为字典 if type(secondDict[key]).__name__ == 'dict': thisDepth = getTreeDepth(secondDict[key]) + 1 else: thisDepth = 1 if thisDepth > maxDepth: maxDepth = thisDepth return maxDepth ''' 在父子节点之间填充文本信息 ''' def plotMidText(cntrPt, parentPt, txtString): xMid = (parentPt[0] - cntrPt[0]) / 2.0 + cntrPt[0] yMid = (parentPt[1] - cntrPt[1]) / 2.0 + cntrPt[1] createPlot.ax1.text(xMid, yMid, txtString) ''' 根节点坐标 ''' def plotTree(myTree, parentPt, nodeTxt): numLeafs = getNumLeafs(myTree) # 子节点数量 depth = getTreeDepth(myTree) # 深度 firstStr = list(myTree.keys())[0] # 根节点的key '''X坐标=节点的x偏移量 + 叶节点数距离 所有该节点下子叶子节点的距离:numLeafs / plotTree.totalW 但是坐标在叶子节点的中心:numLeafs / 2 / plotTree.totalW 又因为xOff初始坐标点在原点的左边:numLeafs / 2 / plotTree.totalW + 0.5 / plotTree.totalW ,这是偏移量 那么x = numLeafs / 2 / plotTree.totalW + 0.5 / plotTree.totalW + plotTree.xOff ''' # 根节点坐标 # 叶子节点距离 cntrPt = (plotTree.xOff + (1.0 + float(numLeafs)) / 2.0 / plotTree.totalw, plotTree.yOff) # 标记子节点属性值 plotMidText(cntrPt, parentPt, nodeTxt) plotNode(firstStr, cntrPt, parentPt, decisionNode) secondDict = myTree[firstStr] plotTree.yOff = plotTree.yOff - 1.0 / plotTree.totalD for key in secondDict.keys(): if type(secondDict[key]).__name__ == 'dict': plotTree(secondDict[key], cntrPt, str(key)) else: plotTree.xOff = plotTree.xOff + 1.0 / plotTree.totalw plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode) plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key)) plotTree.yOff = plotTree.yOff + 1.0 / plotTree.totalD # plot构建树 def createPlot(inTree): # figure语法 创建自定义图像 定义了一个框架 # num:图像编号或名称,数字为编号 # facecolor:背景颜色 fig = plt.figure(1, facecolor='white') #plt.close()将完全关闭图形窗口 # plt.clf()将清除图形-您仍然可以在其上绘制另一个绘图。 fig.clf() # xticks是一个列表,其中的元素就是x轴上将显示的坐标 # yticks是y轴上显示的坐标,这里空列表则不显示坐标 axprops = dict(xticks=[], yticks=[]) # 这里定义一个子图窗口 # 第一个参数xyz含义是,将框架划分为x行y列窗口,ax1代表其第z个窗口。 # ps:111 就是一行一列第一个窗口 # frameon = False将隐藏坐标轴 createPlot.ax1 = plt.subplot(111, frameon=False, **axprops) # plotTree.totalW是决策树的叶子树,也代表宽度 plotTree.totalw = float(getNumLeafs(inTree)) # plotTree.totalD是决策树的深度 plotTree.totalD = float(getTreeDepth(inTree)) # 方便后面加上 1.0 / plotTree.totalW 后位置刚好在中间 plotTree.xOff = -0.5 / plotTree.totalw plotTree.yOff = 1.0 # 调用函数plotTree(),绘制整棵决策树,最后显示出来。 plotTree(inTree, (0.5, 1.0), '') plt.show()
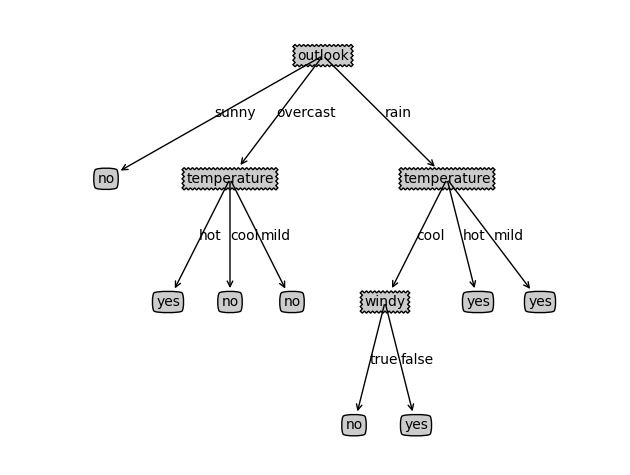
运行结果如下所示:





 浙公网安备 33010602011771号
浙公网安备 33010602011771号