文章相似度算法调研
文章相似度算法大体上分为两类,现实中文本相似性算法分为两类,一类是hash算法,一类是字符串直接匹配算法
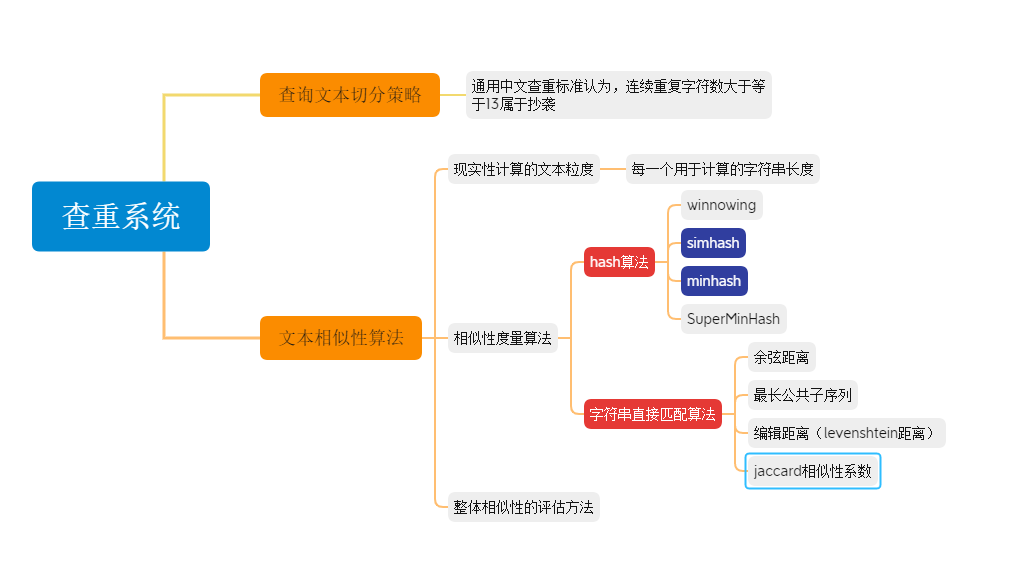
字符串匹配算法在现实情况中由于效率太低一般没人使用,经过调研发现,在实际使用中,几乎所有人都会在simhash和minhash算法中使用其中一种算法计算文本相似度。
一、基本概念
1.TF
TF(term frequency),就是分词出现的频率:该分词在该文档中出现的频率,算法是:(该分词在该文档出现的次数)/(该文档分词的总数),这个值越大表示这个词越重要,即权重就越大。
例如:一篇文档分词后,总共有500个分词,而分词”Hello”出现的次数是20次,则TF值是: tf =20/500=2/50=0.04
2.IDF
IDF(inversedocument frequency)逆向文件频率,一个文档库中,一个分词出现在的文档数越少越能和其它文档区别开来。算法是: log((总文档数/出现该分词的文档数)+0.01) ;(注加上0.01是为了防止log计算返回值为0)。
例如:一个文档库中总共有50篇文档,2篇文档中出现过“Hello”分词,则idf是:
Idf = log(50/2 + 0.01) = log(25.01)=1.39811369
3.TF-IDF
TF-IDF(termfrequency–inverse document frequency)是一种用于资讯检索与资讯探勘的常用加权技术。TF-IDF是一种统计方法,用以评估一字词对于一个文件集或一个语料库中的其中一份文件的重要程度。字词的重要性随著它在文件中出现的次数成正比增加,但同时会随著它在语料库中出现的频率成反比下降。TF-IDF加权的各种形式常被搜寻引擎应用,作为文件与用户查询之间相关程度的度量或评级。除了TF-IDF以外,因特网上的搜寻引擎还会使用基于连结分析的评级方法,以确定文件在搜寻结果中出现的顺序。
在文本挖掘中,要对文本库分词,而分词后需要对个每个分词计算它的权重,而这个权重可以使用TF-IDF计算。
TF-IDF结合计算就是 tf*idf,比如上面的“Hello”分词例子中:
TF-IDF = tf* idf = (20/500)* log(50/2 + 0.01)= 0.04*1.39811369=0.0559245476
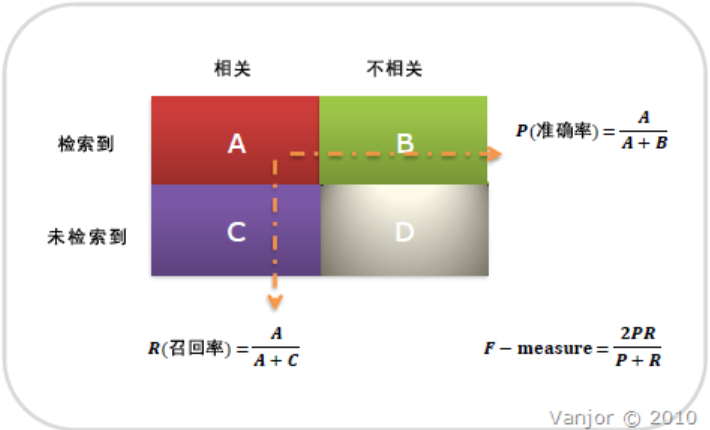
4.准确率和召回率
召回率(Recall Rate,也叫查全率)是检索出的相关文档数和文档库中所有的相关文档数的比率,衡量的是检索系统的查全率;
准确率是检索出的相关文档数与检索出的文档总数的比率,衡量的是检索系统的查准率。
5.编辑距离
编辑距离(Minimum Edit Distance,MED),由俄罗斯科学家 Vladimir Levenshtein 在1965年提出,也因此而得名 Levenshtein Distance。
在信息论、语言学和计算机科学领域,Levenshtein Distance 是用来度量两个序列相似程度的指标。通俗地来讲,编辑距离指的是在两个单词之间,由其中一个单词
转换为另一个单词
所需要的最少单字符编辑操作次数。
在这里定义的单字符编辑操作有且仅有三种:
- 插入(Insertion)
- 删除(Deletion)
- 替换(Substitution)
譬如,"kitten" 和 "sitting" 这两个单词,由 "kitten" 转换为 "sitting" 需要的最少单字符编辑操作有:
1.kitten → sitten (substitution of "s" for "k")
2.sitten → sittin (substitution of "i" for "e")
3.sittin → sitting (insertion of "g" at the end)
因此,"kitten" 和 "sitting" 这两个单词之间的编辑距离为 3 。
6.汉明距离(海明距离)
简单的说,Hamming Distance,又称汉明距离,在信息论中,两个等长字符串之间的汉明距离是两个字符串对应位置的不同字符的个数。也就是说,它就是将一个字符串变换成另外一个字符串所需要替换的字符个数。例如:1011101 与 1001001 之间的汉明距离是 2。至于我们常说的字符串编辑距离则是一般形式的汉明距离。
海明距离的求法:异或时,只有在两个比较的位不同时其结果是1 ,否则结果为0,两个二进制“异或”后得到1的个数即为海明距离的大小。
7.鸽巢原理
桌上有十个苹果,要把这十个苹果放到九个抽屉里,无论怎样放,我们会发现至少会有一个抽屉里面放不少于两个苹果。这一现象就是我们所说的“抽屉原理”。 抽屉原理的一般含义为:“如果每个抽屉代表一个集合,每一个苹果就可以代表一个元素,假如有n+1个元素放到n个集合中去,其中必定有一个集合里至少有两个元素。”
抽屉原理有时也被称为鸽巢原理,它是组合数学中一个重要的原理 。
8.倒排索引
在搜索引擎中每个文件都对应一个文件ID,文件内容被表示为一系列关键词的集合(实际上在搜索引擎索引库中,关键词也已经转换为关键词ID)。例如“文档1”经过分词,提取了20个关键词,每个关键词都会记录它在文档中的出现次数和出现位置。
得到正向索引的结构如下:
“文档1”的ID > 单词1:出现次数,出现位置列表;单词2:出现次数,出现位置列表;…………。
“文档2”的ID > 此文档出现的关键词列表。
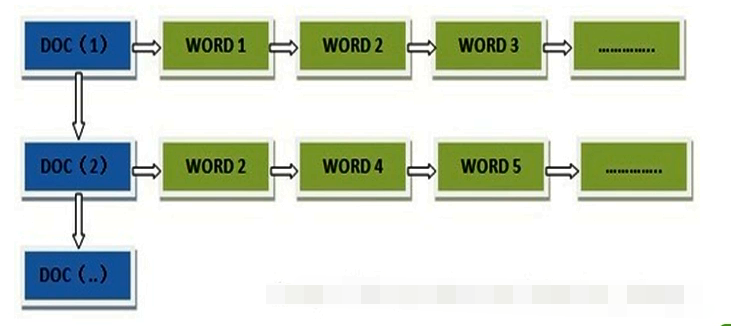
根据正向索引,查找的时候是挨个文档查找对应的关键词,在数据量大的情况下效率会很低,典型的是mysql的like查询方式。
倒排索引则反之,是根据关键词查询文档的技术。
倒排索引的结构如下:
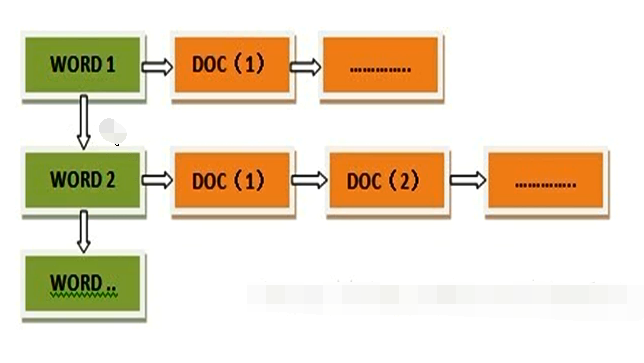
倒排索引的典型应用是ElasticSearch。
二、simhash算法及原理简介
1. 什么是SimHash
SimHash算法是Google在2007年发表的论文《Detecting Near-Duplicates for Web Crawling》中提到的一种指纹生成算法,被应用在Google搜索引擎网页去重的工作之中。
简单的说,SimHash算法主要的工作就是将文本进行降维,生成一个SimHash值,也就是论文中所提及的“指纹”,通过对不同文本的SimHash值进而比较海明距离,从而判断两个文本的相似度。
对于文本去重这个问题,常见的解决办法有余弦算法、欧式距离、Jaccard相似度、最长公共子串等方法。但是这些方法并不能对海量数据高效的处理。
比如说,在搜索引擎中,会有很多相似的关键词,用户所需要获取的内容是相似的,但是搜索的关键词却是不同的,如“北京好吃的火锅“和”哪家北京的火锅好吃“,是两个可以等价的关键词,然而通过普通的hash计算,会产生两个相差甚远的hash串。而通过SimHash计算得到的Hash串会非常的相近,从而可以判断两个文本的相似程度。
2. SimHash的计算原理
SimHash算法主要有五个过程:分词、Hash、加权、合并、降维。
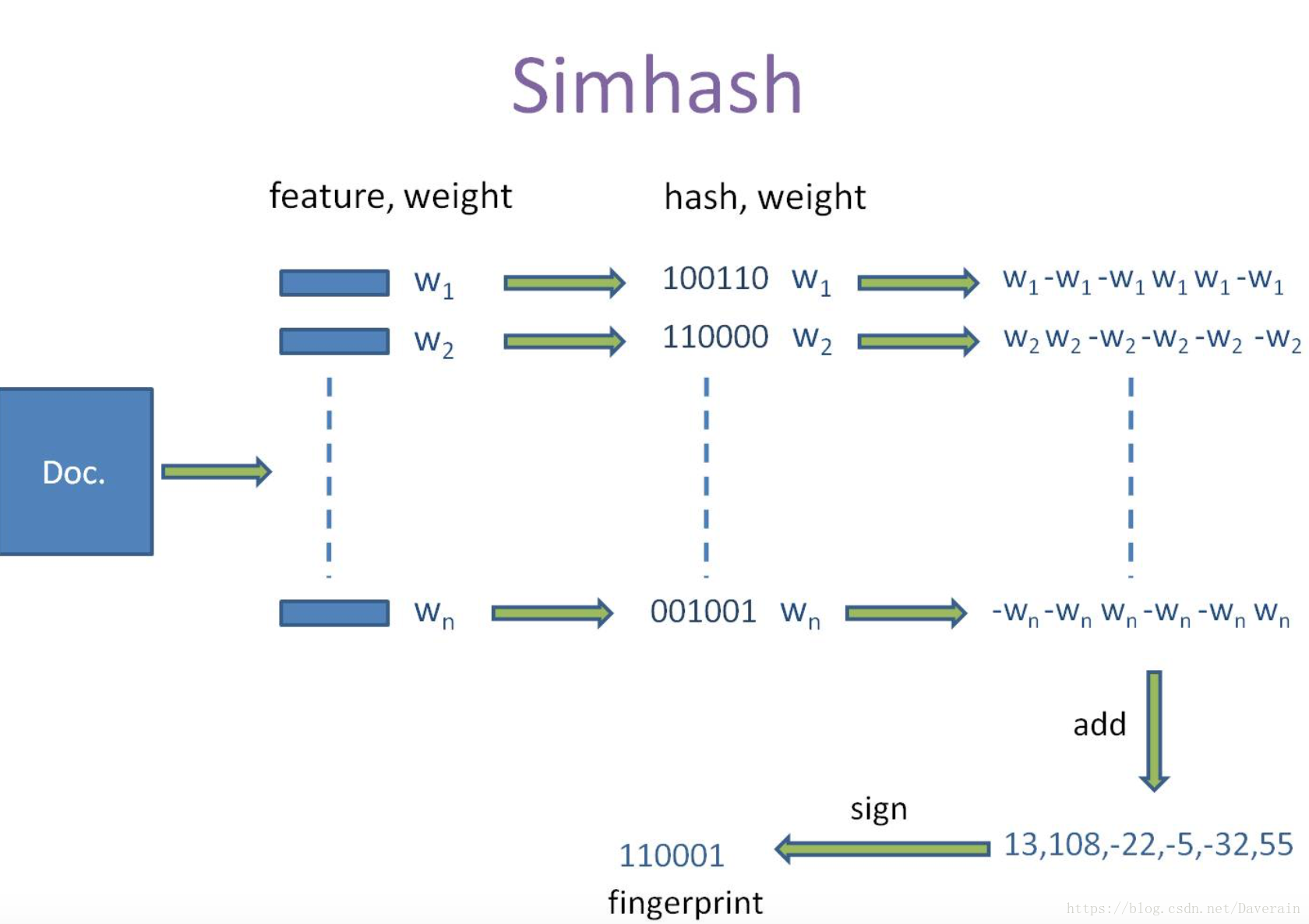
3.步骤
3.1 分词
给定一段语句,进行分词,得到有效的特征向量,然后为每一个特征向量设置1-5等5个级别的权重(如果是给定一个文本,那么特征向量可以是文本中的词,其权重可以是这个词出现的次数)。例如给定一段语句:“CSDN博客结构之法算法之道的作者July”,分词后为:“CSDN 博客 结构 之 法 算法 之 道 的 作者 July”,然后为每个特征向量赋予权值:CSDN(4) 博客(5) 结构(3) 之(1) 法(2) 算法(3) 之(1) 道(2) 的(1) 作者(5) July(5),其中括号里的数字代表这个单词在整条语句中的重要程度,数字越大代表越重要。
计算权重的值可以使用TF-IDF计算。
其中,数字越大,代表特征词在句子中的重要性就越高。这样,我们就得到了一个文本的分词的词向量和每个词向量对应的权重。
3.2 Hash
通过hash函数计算各个特征向量的hash值,hash值为二进制数01组成的n-bit签名。比如“CSDN”的hash值Hash(CSDN)为100101,“博客”的hash值Hash(博客)为“101011”。就这样,字符串就变成了一系列数字。
3.3 加权
前面的计算我们已经得到了每个词向量的Hash串和该词向量对应的权重,这一步我们计算权重向量W=hash*weight,即遇到1则hash值和权值正相乘,遇到0则hash值和权值负相乘。
例如给“CSDN”的hash值“100101”加权得到:W(CSDN) = 100101 * 4 = 4 -4 -4 4 -4 4,给“博客”的hash值“101011”加权得到:W(博客)=101011 * 5 = 5 -5 5 -5 5 5,其余特征向量类似此般操作。
3.4 合并
对于一个文本,我们计算出了文本分词之后每一个特征词的权重向量,在合并这个阶段,我们把文本所有词向量的权重向量相累加,得到一个新的权重向量,拿前两个特征向量举例,例如“CSDN”的“4 -4 -4 4 -4 4”和“博客”的“5 -5 5 -5 5 5”进行累加,得到“4+5 -4+-5 -4+5 4+-5 -4+5 4+5”,得到“9 -9 1 -1 1”。
3.5 降维
对于前面合并后得到的文本的权重向量,如果大于0则置1,否则置0,就可以得到该文本的SimHash值。最后我们便可以根据不同语句simhash的海明距离来判断它们的相似度。例如把上面计算出来的“9 -9 1 -1 1 9”降维(某位大于0记为1,小于0记为0),得到的01串为:“1 0 1 0 1 1”,从而形成它们的simhash签名。
到此为止,我们已经计算出了一个文本的SimHash值。那么,如何判断两个文本是否相似呢?我们要用到海明距离。
3.6 相似度判断
一般来说SimHash值是一个64位的长整数,作为对应文本的签名,从经验上来看,只要找到海明距离在3以内的所有签名,即可找出所有相似的文本。
4. 海量数据下的汉明距离计算
如何扩展到海量数据呢?譬如如何在海量的样本库中查询与其海明距离在3以内的记录呢?
一种方案是,查找待查询文本的64位simhash code的所有3位以内变化的组合:大约需要四万多次的查询。
另一种方案是,预生成库中所有样本simhash code的3位变化以内的组合:大约需要占据4万多倍的原始空间。
这两种方案,要么时间复杂度高,要么空间复杂度复杂,能否有一种方案可以达到时空复杂度的绝佳平衡呢?答案是肯定的,这时候有一种较好的办法来均衡计算海明距离的时间复杂度和空间复杂度,具体的计算思想是这样的:
我们可以把 64 位的二进制simhash签名均分成4块,每块16位。根据鸽巢原理(也称抽屉原理),如果两个SimHash相似,即两个签名的海明距离在 3 以内,它们必有一块完全相同。
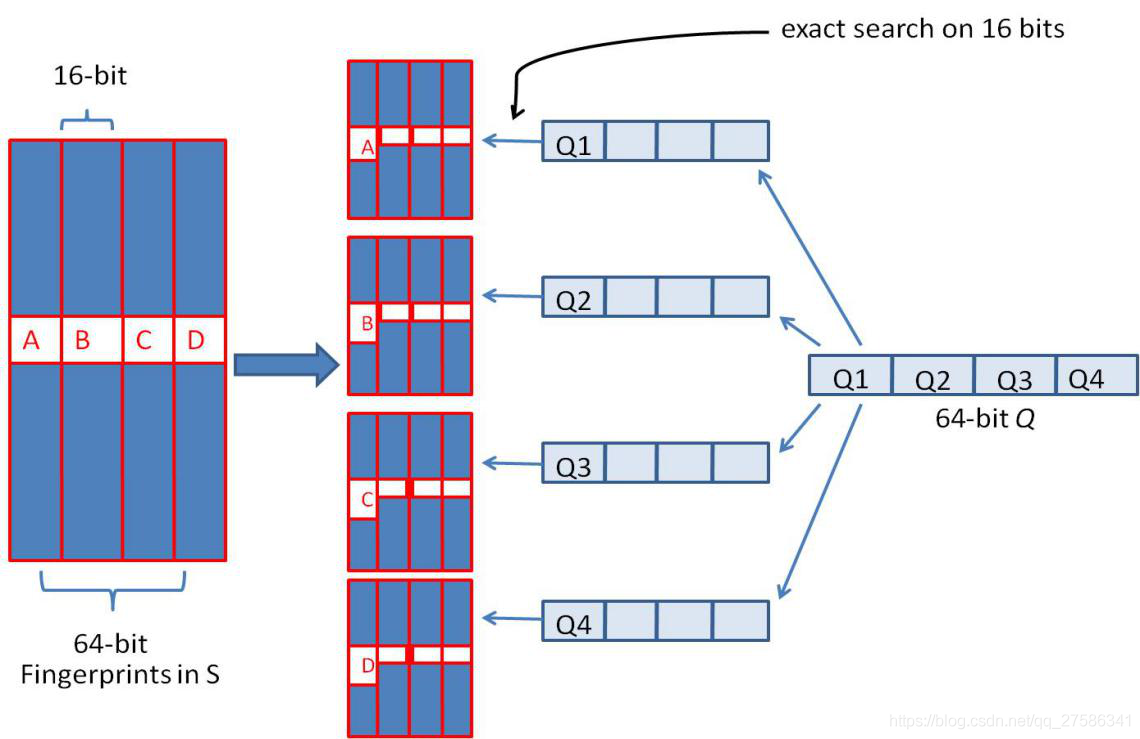
把分成的4 块中的每一个块分别作为前16位来进行查找,建倒排索引。
三、Minhash算法及原理介绍
给出N个集合,找到相似的集合对,如何实现呢?直观的方法是比较任意两个集合。那么可以十分精确的找到每一对相似的集合,但是时间复杂度是\(O(n^2)\)。当N比较小时,比如K级,此算法可以在接受的时间范围内完成,但是如果N变大时,比B级,甚至P级,那么需要的时间是不能够被接受的。比如N= 1B = 1,000,000,000。一台计算机每秒可以比较1,000,000,000对集合是否相等。那么大概需要15年的时间才能找到所有相似的集合!
上面的算法虽然效率很低,但是结果会很精确,因为检查了每一对集合。假如,N个集合中只有少数几对集合相似,绝大多数集合都不等呢?那么根据上述算法,绝大多数检测的结果是两个结合不相似,可以说这些检测“浪费了计算时间”。所以,如果能找到一种算法,将大体上相似的集合聚到一起,缩小比对的范围,这样只用检测较少的集合对,就可以找到绝大多数相似的集合对,大幅度减少时间开销。虽然牺牲了一部分精度,但是如果能够将时间大幅度减少,这种算法还是可以接受的。接下来的内容讲解如何使用Minhash和LSH(Locality-sensitive Hashing)来实现上述目的,在相似的集合较少的情况下,可以在\(O(n)\)时间找到大部分相似的集合对。
1.Jaccard相似度
判断两个集合是否相等,一般使用称之为Jaccard相似度的算法(后面用Jac(S1,S2)来表示集合S1和S2的Jaccard相似度)。举个列子,集合X = {a,b,c},Y = {b,c,d}。那么Jac(X,Y) = 2 / 3 = 0.67。也就是说,结合X和Y有67%的元素相同。下面是形式的表述Jaccard相似度公式:
也就是两个集合交集的个数比上两个集合并集的个数。范围在[0,1]之间。
2.降维技术Minhash
原始问题的关键在于计算时间太长。所以,如果能够找到一种很好的方法将原始集合压缩成更小的集合,而且又不失去相似性,那么可以缩短计算时间。Minhash可以帮助我们解决这个问题。举个例子,\(S1 = \{a,d,e\}\),\(S2 = \{c, e\}\),设全集\(U = \{a,b,c,d,e\}\)。集合可以如下表示:
| 行号 | 元素 | S1 | S2 | 类别 |
|---|---|---|---|---|
| 1 | a | 1 | 0 | Y |
| 2 | b | 0 | 0 | Z |
| 3 | c | 0 | 1 | Y |
| 4 | d | 1 | 0 | Y |
| 5 | e | 1 | 1 | X |
表1中,列表示集合,行表示元素,值1表示某个集合具有某个值,0则相反(X,Y,Z的意义后面讨论)。Minhash算法大体思路是:采用一种hash函数,将元素的位置均匀打乱,然后将新顺序下每个集合第一个值为1的元素作为该集合的特征值。比如哈希函数\(h_{1}(i) = (i + 1)\% 5\),其中i为行号。作用于集合S1和S2,得到如下结果:
| 行号 | 元素 | S1 | S2 | 类别 |
|---|---|---|---|---|
| 1 | e | 1 | 1 | X |
| 2 | a | 1 | 0 | Y |
| 3 | b | 0 | 0 | Z |
| 4 | c | 0 | 1 | Y |
| 5 | d | 1 | 0 | Y |
| Minhash | e | e |
这时,Minhash(S1) = e,Minhash(S2) = e。也就是说用元素e表示S1,用元素e表示集合S2。那么这样做是否科学呢?也就是说,如果Minhash(S1) 等于Minhash(S2),那么S1是否和S2类似呢?
3.一个神奇的结论
在哈希函数\(h_{1}\)均匀分布的情况下,集合\(S1\)的Minhash值和集合\(S2\)的Minhash值相等的概率等于集合\(S1\)与集合\(S2\)的Jaccard相似度,下面简单分析一下这个结论。
S1和S2的每一行元素可以分为三类:
-
X类 均为1。比如表2中的第1行,两个集合都有元素e。
-
Y类 一个为1,另一个为0。比如表2中的第2行,表明S1有元素a,而S2没有。
-
Z类 均为0。比如表2中的第3行,两个集合都没有元素b。
这里忽略所有Z类的行,因为此类行对两个集合是否相似没有任何贡献。由于哈希函数将原始行号均匀分布到新的行号,这样可以认为在新的行号排列下,任意一行出现X类的情况的概率为
这里为了方便,将任意位置设为第一个出现X类行的行号。所以
这里很重要的一点就是要保证哈希函数可以将数值均匀分布,尽量减少冲撞。
一般而言,会找出一系列的哈希函数,比如h个(h << |U|),为每一个集合计算h次Minhash值,然后用h个Minhash值组成一个摘要来表示当前集合(注意Minhash的值的位置需要保持一致)。举个列子,还是基于上面的例子,现在又有一个哈希函数h2(i) = (i -1)% 5。那么得到如下集合:
| 行号 | 元素 | S1 | S2 | 类别 |
|---|---|---|---|---|
| 1 | b | 0 | 0 | Z |
| 2 | c | 0 | 1 | Y |
| 3 | d | 1 | 0 | Y |
| 4 | e | 1 | 1 | X |
| 5 | a | 1 | 0 | Y |
| Minhash | d | c |
所以,现在用摘要表示的原始集合如下:
| 哈希函数 | S1 | S2 |
|---|---|---|
| h1(i) = (i + 1) % 5 | e | e |
| h2(i) = (i - 1) % 5 | d | c |
从上表还可以得到一个结论,令X表示Minhash摘要后的集合对应行相等的次数(比如上表,X=1,因为哈希函数h1情况下,两个集合的minhash相等,h2不等):
X符合次数为h,概率为Jac(S1,S2)的二项分布。那么期望E(X) = h * Jac(S1,S2) = 2 * 2 / 3 = 1.33。也就是每2个hash计算Minhash摘要,可以期望有1.33元素对应相等。
所以,Minhash在压缩原始集合的情况下,保证了集合的相似度没有被破坏。
4.LSH – 局部敏感哈希
现在有了原始集合的摘要,但是还是没有解决最初的问题,仍然需要遍历所有的集合对,,才能所有相似的集合对,复杂度仍然是\(O(n^2)\)。所以,接下来描述解决这个问题的核心思想LSH。其基本思路是将相似的集合聚集到一起,减小查找范围,避免比较不相似的集合。仍然是从例子开始,现在有5个集合,计算出对应的Minhash摘要,如下:
| S1 | S2 | S3 | S4 | S5 | |
|---|---|---|---|---|---|
| 区间1 | b | b | a | b | a |
| c | c | a | c | b | |
| d | b | a | d | c | |
| 区间2 | a | e | b | e | d |
| b | d | c | f | e | |
| e | a | d | g | a | |
| 区间3 | d | c | a | h | b |
| a | a | b | b | a | |
| d | e | a | b | e | |
| 区间4 | d | a | a | c | b |
| b | a | c | b | a | |
| d | e | a | b | e |
上面的集合摘要采用了12个不同的hash函数计算出来,然后分成了B = 4个区间。前面已经分析过,任意两个集合(S1,S2)对应的Minhash值相等的概率\(r = Jac(S1,S2)\)。先分析区间1,在这个区间内,\(P(集合S1等于集合S2) = r3\)。所以只要S1和S2的Jaccard相似度越高,在区间1内越有可能完成全一致,反过来也一样。那么\(P(集合S1不等于集合S2) = 1 - r3\)。现在有4个区间,其他区间与第一个相同,所以
这里的概率是一个r的函数,形状犹如一个S型,如下:
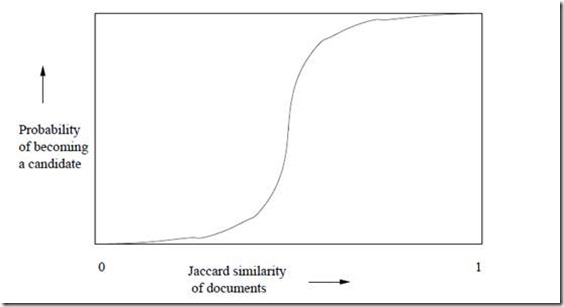
如果令区间个数为B,每个区间内的行数为C,那么上面的公式可以形式的表示为:
令r = 0.4,C=3,B = 100。上述公式计算的概率为0.9986585。这表明两个Jaccard相似度为0.4的集合在至少一个区间内冲撞的概率达到了99.9%。根据这一事实,我们只需要选取合适的B和C,和一个冲撞率很低的hash函数,就可以将相似的集合至少在一个区间内冲撞,这样也就达成了本节最开始的目的:将相似的集合放到一起。具体的方法是为B个区间,准备B个hash表,和区间编号一一对应,然后用hash函数将每个区间的部分集合映射到对应hash表里。最后遍历所有的hash表,将冲撞的集合作为候选对象进行比较,找出相识的集合对。整个过程是采用\(O(n)\)的时间复杂度,因为B和C均是常量。由于聚到一起的集合相比于整体比较少,所以在这小范围内互相比较的时间开销也可以计算为常量,那么总体的计算时间也是\(O(n)\)。
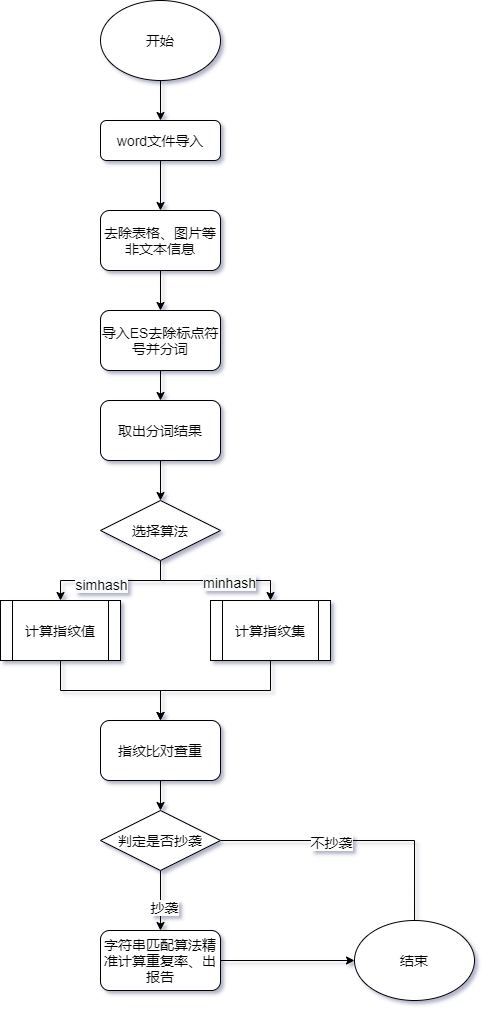
四、实践
参考文档
Choosing between SimHash and MinHash for a production system
Elasticsearch: getting the tf-idf of every term in a given document
Document Deduplication with Locality Sensitive Hashing
Near-Duplicate Detection using MinHash: Background
[Document Deduplication][1] MinHash
[Document Deduplication][2] Locality Sensitive Hashing
how-scoring-works-in-elasticsearch
相关论文
SuperMinHash – A New Minwise Hashing Algorithm for Jaccard Similarity Estimation


 浙公网安备 33010602011771号
浙公网安备 33010602011771号