HDU 4498 Function Curve (自适应simpson)
Function Curve
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65535/65535 K (Java/Others)
Total Submission(s): 203 Accepted Submission(s): 67
Problem Description
Given sequences of k1, k2, … kn, a1, a2, …, an and b1, b2, …, bn. Consider following function:
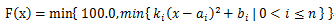
Then we draw F(x) on a xy-plane, the value of x is in the range of [0,100]. Of course, we can get a curve from that plane.
Can you calculate the length of this curve?
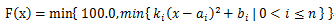
Then we draw F(x) on a xy-plane, the value of x is in the range of [0,100]. Of course, we can get a curve from that plane.
Can you calculate the length of this curve?
Input
The first line of the input contains one integer T (1<=T<=15), representing the number of test cases.
Then T blocks follow, which describe different test cases.
The first line of a block contains an integer n ( 1 <= n <= 50 ).
Then followed by n lines, each line contains three integers ki, ai, bi ( 0<=ai, bi<100, 0<ki<100 ) .
Then T blocks follow, which describe different test cases.
The first line of a block contains an integer n ( 1 <= n <= 50 ).
Then followed by n lines, each line contains three integers ki, ai, bi ( 0<=ai, bi<100, 0<ki<100 ) .
Output
For each test case, output a real number L which is rounded to 2 digits after the decimal point, means the length of the curve.
Sample Input
2
3
1 2 3
4 5 6
7 8 9
1
4 5 6
Sample Output
215.56
278.91
Hint
All test cases are generated randomly.
Source
Recommend
liuyiding
数值方法计算积分
1 /* *********************************************** 2 Author :kuangbin 3 Created Time :2013-10-9 12:04:07 4 File Name :E:\2013ACM\专题学习\数学\积分\HDU4498.cpp 5 ************************************************ */ 6 7 #include <stdio.h> 8 #include <string.h> 9 #include <iostream> 10 #include <algorithm> 11 #include <vector> 12 #include <queue> 13 #include <set> 14 #include <map> 15 #include <string> 16 #include <math.h> 17 #include <stdlib.h> 18 #include <time.h> 19 using namespace std; 20 21 vector<double>x; 22 23 void add(int a1,int b1,int c1)//计算a1*x^2 + b1*x + c = 0的解 24 { 25 if(a1 == 0 && b1 == 0) 26 { 27 return; 28 } 29 if(a1 == 0) 30 { 31 double t = -c1*1.0/b1; 32 if(t >= 0 && t <= 100) 33 x.push_back(t); 34 return; 35 } 36 long long deta = b1*b1 - 4LL*a1*c1; 37 if(deta < 0)return; 38 if(deta == 0) 39 { 40 double t = (-1.0 * b1)/(2.0 * a1); 41 if(t >= 0 && t <= 100) 42 x.push_back(t); 43 } 44 else 45 { 46 double t1 = (-1.0 * b1 + sqrt(1.0*deta))/(2.0*a1); 47 double t2 = (-1.0 * b1 - sqrt(1.0*deta))/(2.0*a1); 48 if(t1 >= 0 && t1 <= 100) 49 x.push_back(t1); 50 if(t2 >= 0 && t2 <= 100) 51 x.push_back(t2); 52 } 53 } 54 int A[100],B[100],C[100]; 55 int best; 56 double F(double x1) 57 { 58 return sqrt(1.0 + (x1*2*A[best] + 1.0 * B[best])*(x1*2*A[best] + 1.0 * B[best])); 59 } 60 double simpson(double a,double b) 61 { 62 double c = a + (b-a)/2; 63 return (F(a) + 4*F(c) + F(b))*(b-a)/6; 64 } 65 double asr(double a,double b,double eps,double A) 66 { 67 double c = a + (b-a)/2; 68 double L = simpson(a,c); 69 double R = simpson(c,b); 70 if(fabs(L+R-A) <= 15*eps)return L+R+(L+R-A)/15; 71 return asr(a,c,eps/2,L) + asr(c,b,eps/2,R); 72 } 73 double asr(double a,double b,double eps) 74 { 75 return asr(a,b,eps,simpson(a,b)); 76 } 77 78 int main() 79 { 80 //freopen("in.txt","r",stdin); 81 //freopen("out.txt","w",stdout); 82 int T; 83 int k,a,b; 84 scanf("%d",&T); 85 while(T--) 86 { 87 int n; 88 scanf("%d",&n); 89 A[0] = 0; 90 B[0] = 0; 91 C[0] = 100; 92 for(int i = 1;i <= n;i++) 93 { 94 scanf("%d%d%d",&k,&a,&b); 95 A[i] = k; 96 B[i] = -2*a*k; 97 C[i] = k*a*a + b; 98 } 99 x.clear(); 100 for(int i = 0;i <= n;i++) 101 for(int j = i+1;j <= n;j++) 102 add(A[i]-A[j],B[i] - B[j],C[i] - C[j]); 103 double ans = 0; 104 x.push_back(0); 105 x.push_back(100); 106 sort(x.begin(),x.end()); 107 int sz = x.size(); 108 for(int i = 0;i < sz-1;i++) 109 { 110 double x1 = x[i]; 111 double x2 = x[i+1]; 112 if(fabs(x2-x1) < 1e-8)continue; 113 double mid = (x1 + x2)/2; 114 best = 0; 115 for(int j = 1;j <= n;j++) 116 { 117 double tmp1 = mid*mid*A[best] + mid*B[best] + C[best]; 118 double tmp2 = mid*mid*A[j] + mid*B[j] + C[j]; 119 if(tmp2 < tmp1)best = j; 120 } 121 ans += asr(x1,x2,1e-8); 122 } 123 printf("%.2lf\n",ans); 124 } 125 return 0; 126 }
人一我百!人十我万!永不放弃~~~怀着自信的心,去追逐梦想

 浙公网安备 33010602011771号
浙公网安备 33010602011771号