HDU 4024 Dwarven Sniper’s hunting(数学公式 或者是二分)
Dwarven Sniper’s hunting
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65768/65768 K (Java/Others)
Total Submission(s): 441 Accepted Submission(s): 199
Problem Description
Now the hunting starts in the world named DOTA, a stupid PC game which cannot play with others together.
Among the individuals in the game, there are two heroes named Dwarven Sniper and Lycanthrope. Lycanthrope wants to escape from being captured; however, our Dwarven Sniper won’t let him go! He will use the Silver Bullet to kill the Lycanthrope by only one shot! Yes, that’s enough.
Lycanthrope is running on a line in the map with a constant speed and direction. The weapon range of the Silver Bullet is limited by L meters. Dwarven Sniper can run for a while freely, and then shoot Lycanthrope. In order to show his excellent shooting skill, Dwarven Sniper wants the Silver Bullet flying as far as possible. But don’t forget the flying time of the Silver Bullet due to considerable weight of the bullet. And Dwarven Sniper wants to stop the hunting as quickly as possible. So if there is more than one way to show his excellent skill, he would choose the fastest way. In this problem we consider the Silver Bullet and Lycanthrope as two points.
Now Dwarven Sniper wants to know the maximum length that the Silver Bullet can fly, and the shortest time that the hunting lasts. Specifically, the total hunting time is defined as the time interval from the start of hunting to the moment that the bullet hit Lycanthrope. Can you help him?
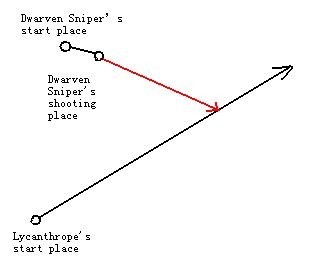
Among the individuals in the game, there are two heroes named Dwarven Sniper and Lycanthrope. Lycanthrope wants to escape from being captured; however, our Dwarven Sniper won’t let him go! He will use the Silver Bullet to kill the Lycanthrope by only one shot! Yes, that’s enough.
Lycanthrope is running on a line in the map with a constant speed and direction. The weapon range of the Silver Bullet is limited by L meters. Dwarven Sniper can run for a while freely, and then shoot Lycanthrope. In order to show his excellent shooting skill, Dwarven Sniper wants the Silver Bullet flying as far as possible. But don’t forget the flying time of the Silver Bullet due to considerable weight of the bullet. And Dwarven Sniper wants to stop the hunting as quickly as possible. So if there is more than one way to show his excellent skill, he would choose the fastest way. In this problem we consider the Silver Bullet and Lycanthrope as two points.
Now Dwarven Sniper wants to know the maximum length that the Silver Bullet can fly, and the shortest time that the hunting lasts. Specifically, the total hunting time is defined as the time interval from the start of hunting to the moment that the bullet hit Lycanthrope. Can you help him?

Input
There are several test cases. Each of them contains only one line which consist of 9 real numbers, that are X1, Y1, X2, Y2, Lx, Ly, vD , vB and L (-10000 <= X1 , Y1 , X2 , Y2 , Lx , Ly <= 10000 , 0 <= vD , vB , L <=100000).
The pair (X1, Y1) is the starting position of the Lycanthrope while (X2, Y2) is the starting position of Dwarven Sniper.
(Lx, Ly) is the moving vector per second of the Lycanthrope.
vD is the speed of the Dwarven Sniper .
vB is the speed of the Silver Bullet.
All units are meters/second.
It is guaranteed that (Lx*Lx+Ly*Ly) < vD*vD < vB*vB , and Dwarven Sniper’s starting position is different from Lycanthrope’s position. The input ends with a line containing all zeros.
The pair (X1, Y1) is the starting position of the Lycanthrope while (X2, Y2) is the starting position of Dwarven Sniper.
(Lx, Ly) is the moving vector per second of the Lycanthrope.
vD is the speed of the Dwarven Sniper .
vB is the speed of the Silver Bullet.
All units are meters/second.
It is guaranteed that (Lx*Lx+Ly*Ly) < vD*vD < vB*vB , and Dwarven Sniper’s starting position is different from Lycanthrope’s position. The input ends with a line containing all zeros.
Output
For each test case, output two real numbers S and T in a line separated by a single space denoting that the Silver bullet flies S meters before hitting Lycanthrope and the hunting lasts for T seconds, both with 3 digits after the decimal point.
You may assume that Dwarven Sniper can finish his hunting within no more than 1e+9 seconds.
You may assume that Dwarven Sniper can finish his hunting within no more than 1e+9 seconds.
Sample Input
-1 0 0 10 1 0 2 10 10 0 0 0 5 0 1 2 6 6 0 0 0 0 0 0 0 0 0
Sample Output
10.000 1.000 6.000 3.000
Source
Recommend
lcy
此题是比较有意思的题目。。上一年网络赛的时候竟然会没有做出来~~~~
我用了两种方法去做这题
一种是直接根据公式计算的,另外一种是二分算出来的。两种方法速度都很快,充分体会到二分的效率之高啊~~~
题目中一个很重要的条件就是 (Lx*Lx+Ly*Ly) < vD*vD < vB*vB ,
这样说明一定是可以追上的,而且可以以最大的距离射中,所以第一问的答案一定就是L的。
假设追击者跑的时间是 t1,那么肯定子弹飞行时间就是 L/vB 了
那么此时被追击者的位置就是 A(x1+(t1+L/vB)*Lx,y1+(t1+L/vB)*Ly )了
那么 点 (x2,y2) 到点A的距离等于 L+vD*t1 或者是 L-vD*t1
联立一个一元二次方程,很容易解出来。上面有两个方程,可以求得4个解。
那么选择其中最小的非负解就是答案了。
注意最后时间要加上 L/vB
看代码:
/* HDU 4024 找数学公式计算 */ #include<stdio.h> #include<iostream> #include<math.h> #include<string.h> using namespace std; int main() { //freopen("D.in","r",stdin); //freopen("D.out","w",stdout); double x1,y1,x2,y2,Lx,Ly,vD,vB,L; while(scanf("%lf%lf%lf%lf%lf%lf%lf%lf%lf",&x1,&y1,&x2,&y2,&Lx,&Ly,&vD,&vB,&L)) { if(x1==0&&y1==0&&x2==0&&y2==0&&Lx==0&&Ly==0&&vD==0&&vB==0&&L==0)break; double a=vD*vD-Lx*Lx-Ly*Ly; double b=2*L*vD-2*Lx*(x1-x2+L*Lx/vB)-2*Ly*(y1-y2+L*Ly/vB); double c=L*L-(x1-x2+L*Lx/vB)*(x1-x2+L*Lx/vB)-(y1-y2+L*Ly/vB)*(y1-y2+L*Ly/vB); double s1=(-b-sqrt(b*b-4*a*c))/(2*a); double s2=(-b+sqrt(b*b-4*a*c))/(2*a); b=-2*L*vD-2*Lx*(x1-x2+L*Lx/vB)-2*Ly*(y1-y2+L*Ly/vB); double s3=(-b-sqrt(b*b-4*a*c))/(2*a); double s4=(-b+sqrt(b*b-4*a*c))/(2*a); printf("%.3lf ",L); //从s1 s2 s3 s4当中选出一个最小的正数 if(s1<0)s1=10000000000.0; if(s2<0)s2=10000000000.0; if(s3<0)s3=10000000000.0; if(s4<0)s4=10000000000.0; printf("%.3lf\n",min(s1,min(s2,min(s3,s4)))+L/vB);//不要忘记加上L/vB } return 0; }
再附上二分做法的代码。
思路是差不多的。就是用二分来确定那个时间。
/* HDU 4024 二分 */ #include<stdio.h> #include<iostream> #include<math.h> #include<algorithm> using namespace std; const double eps=1e-8;//1e-6会WR const double INF=1e9; int main() { //freopen("D.in","r",stdin); //freopen("D.out","w",stdout); double x1,y1,x2,y2,Lx,Ly,vD,vB,L; while(scanf("%lf%lf%lf%lf%lf%lf%lf%lf%lf",&x1,&y1,&x2,&y2,&Lx,&Ly,&vD,&vB,&L)) { if(x1==0&&y1==0&&x2==0&&y2==0&&Lx==0&&Ly==0&&vD==0&&vB==0&&L==0)break; double l=0; double r=INF; double mid; double x,y; while(l<r-eps) { mid=(l+r)/2; x=x1+mid*Lx; y=y1+mid*Ly; double d=sqrt((x-x2)*(x-x2)+(y-y2)*(y-y2));//两点距离 double d1=vD*(mid-L/vB);//勇士跑的最大距离 if(d<=L)//在圆里面 { if(d+d1<=L)l=mid;//到不了圆周上 else r=mid; } else { if(L+d1<=d)l=mid;//到不了圆周上 else r=mid; } } printf("%.3lf %.3lf\n",L,mid); } return 0; }
人一我百!人十我万!永不放弃~~~怀着自信的心,去追逐梦想

 浙公网安备 33010602011771号
浙公网安备 33010602011771号