HDU 3662 3D Convex Hull (三维凸包,求凸包多边形个数)
3D Convex Hull
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 592 Accepted Submission(s): 328
Problem Description
There are N points in 3D-space which make up a 3D-Convex hull*. How many faces does the 3D-convexhull have? It is guaranteed that all the points are not in the same plane.
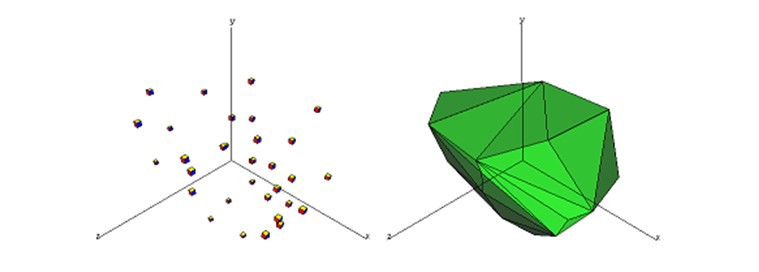
In case you don’t know the definition of convex hull, here we give you a clarification from Wikipedia:
*Convex hull: In mathematics, the convex hull, for a set of points X in a real vector space V, is the minimal convex set containing X.

In case you don’t know the definition of convex hull, here we give you a clarification from Wikipedia:
*Convex hull: In mathematics, the convex hull, for a set of points X in a real vector space V, is the minimal convex set containing X.
Input
There are several test cases. In each case the first line contains an integer N indicates the number of 3D-points (3< N <= 300), and then N lines follow, each line contains three numbers x, y, z (between -10000 and 10000) indicate the 3d-position of a point.
Output
Output the number of faces of the 3D-Convex hull.
Sample Input
7 1 1 0 1 -1 0 -1 1 0 -1 -1 0 0 0 1 0 0 0 0 0 -0.1 7 1 1 0 1 -1 0 -1 1 0 -1 -1 0 0 0 1 0 0 0 0 0 0.1
Sample Output
8 5
Source
Recommend
lcy
直接套模板:
/* HDU 3662 求凸包表面多边形个数 */ #include<stdio.h> #include<algorithm> #include<string.h> #include<math.h> #include<stdlib.h> using namespace std; const int MAXN=550; const double eps=1e-8; struct Point { double x,y,z; Point(){} Point(double xx,double yy,double zz):x(xx),y(yy),z(zz){} //两向量之差 Point operator -(const Point p1) { return Point(x-p1.x,y-p1.y,z-p1.z); } //两向量之和 Point operator +(const Point p1) { return Point(x+p1.x,y+p1.y,z+p1.z); } //叉乘 Point operator *(const Point p) { return Point(y*p.z-z*p.y,z*p.x-x*p.z,x*p.y-y*p.x); } Point operator *(double d) { return Point(x*d,y*d,z*d); } Point operator / (double d) { return Point(x/d,y/d,z/d); } //点乘 double operator ^(Point p) { return (x*p.x+y*p.y+z*p.z); } }; struct CH3D { struct face { //表示凸包一个面上的三个点的编号 int a,b,c; //表示该面是否属于最终凸包上的面 bool ok; }; //初始顶点数 int n; //初始顶点 Point P[MAXN]; //凸包表面的三角形数 int num; //凸包表面的三角形 face F[8*MAXN]; //凸包表面的三角形 int g[MAXN][MAXN]; //向量长度 double vlen(Point a) { return sqrt(a.x*a.x+a.y*a.y+a.z*a.z); } //叉乘 Point cross(const Point &a,const Point &b,const Point &c) { return Point((b.y-a.y)*(c.z-a.z)-(b.z-a.z)*(c.y-a.y), (b.z-a.z)*(c.x-a.x)-(b.x-a.x)*(c.z-a.z), (b.x-a.x)*(c.y-a.y)-(b.y-a.y)*(c.x-a.x) ); } //三角形面积*2 double area(Point a,Point b,Point c) { return vlen((b-a)*(c-a)); } //四面体有向体积*6 double volume(Point a,Point b,Point c,Point d) { return (b-a)*(c-a)^(d-a); } //正:点在面同向 double dblcmp(Point &p,face &f) { Point m=P[f.b]-P[f.a]; Point n=P[f.c]-P[f.a]; Point t=p-P[f.a]; return (m*n)^t; } void deal(int p,int a,int b) { int f=g[a][b];//搜索与该边相邻的另一个平面 face add; if(F[f].ok) { if(dblcmp(P[p],F[f])>eps) dfs(p,f); else { add.a=b; add.b=a; add.c=p;//这里注意顺序,要成右手系 add.ok=true; g[p][b]=g[a][p]=g[b][a]=num; F[num++]=add; } } } void dfs(int p,int now)//递归搜索所有应该从凸包内删除的面 { F[now].ok=0; deal(p,F[now].b,F[now].a); deal(p,F[now].c,F[now].b); deal(p,F[now].a,F[now].c); } bool same(int s,int t) { Point &a=P[F[s].a]; Point &b=P[F[s].b]; Point &c=P[F[s].c]; return fabs(volume(a,b,c,P[F[t].a]))<eps && fabs(volume(a,b,c,P[F[t].b]))<eps && fabs(volume(a,b,c,P[F[t].c]))<eps; } //构建三维凸包 void create() { int i,j,tmp; face add; num=0; if(n<4)return; //********************************************** //此段是为了保证前四个点不共面 bool flag=true; for(i=1;i<n;i++) { if(vlen(P[0]-P[i])>eps) { swap(P[1],P[i]); flag=false; break; } } if(flag)return; flag=true; //使前三个点不共线 for(i=2;i<n;i++) { if(vlen((P[0]-P[1])*(P[1]-P[i]))>eps) { swap(P[2],P[i]); flag=false; break; } } if(flag)return; flag=true; //使前四个点不共面 for(int i=3;i<n;i++) { if(fabs((P[0]-P[1])*(P[1]-P[2])^(P[0]-P[i]))>eps) { swap(P[3],P[i]); flag=false; break; } } if(flag)return; //***************************************** for(i=0;i<4;i++) { add.a=(i+1)%4; add.b=(i+2)%4; add.c=(i+3)%4; add.ok=true; if(dblcmp(P[i],add)>0)swap(add.b,add.c); g[add.a][add.b]=g[add.b][add.c]=g[add.c][add.a]=num; F[num++]=add; } for(i=4;i<n;i++) { for(j=0;j<num;j++) { if(F[j].ok&&dblcmp(P[i],F[j])>eps) { dfs(i,j); break; } } } tmp=num; for(i=num=0;i<tmp;i++) if(F[i].ok) F[num++]=F[i]; } //表面积 double area() { double res=0; if(n==3) { Point p=cross(P[0],P[1],P[2]); res=vlen(p)/2.0; return res; } for(int i=0;i<num;i++) res+=area(P[F[i].a],P[F[i].b],P[F[i].c]); return res/2.0; } double volume() { double res=0; Point tmp(0,0,0); for(int i=0;i<num;i++) res+=volume(tmp,P[F[i].a],P[F[i].b],P[F[i].c]); return fabs(res/6.0); } //表面三角形个数 int triangle() { return num; } //表面多边形个数 int polygon() { int i,j,res,flag; for(i=res=0;i<num;i++) { flag=1; for(j=0;j<i;j++) if(same(i,j)) { flag=0; break; } res+=flag; } return res; } //三维凸包重心 Point barycenter() { Point ans(0,0,0),o(0,0,0); double all=0; for(int i=0;i<num;i++) { double vol=volume(o,P[F[i].a],P[F[i].b],P[F[i].c]); ans=ans+(o+P[F[i].a]+P[F[i].b]+P[F[i].c])/4.0*vol; all+=vol; } ans=ans/all; return ans; } //点到面的距离 double ptoface(Point p,int i) { return fabs(volume(P[F[i].a],P[F[i].b],P[F[i].c],p)/vlen((P[F[i].b]-P[F[i].a])*(P[F[i].c]-P[F[i].a]))); } }; CH3D hull; int main() { // freopen("in.txt","r",stdin); // freopen("out.txt","w",stdout); while(scanf("%d",&hull.n)==1) { for(int i=0;i<hull.n;i++) { scanf("%lf%lf%lf",&hull.P[i].x,&hull.P[i].y,&hull.P[i].z); } hull.create(); printf("%d\n",hull.polygon()); } return 0; }
人一我百!人十我万!永不放弃~~~怀着自信的心,去追逐梦想


