二分图
1. 二分图的概念
二分图,又称二部图,英文名叫 Bipartite graph。
如果一张无向图的 \(N\ (N≥2)\) 个节点,可以分成 A、B 两个非空集合,其中 \(A∩B=Φ\),并且在同一集合内的点之间都没有边相连,那么称这张无向图为一张二分图。A、B 分别称为二分图的 左部 和 右部。如下图所示。
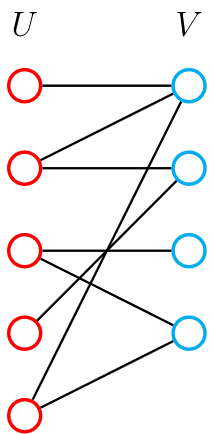
2. 二分图的判定
如果两个集合中的点分别染成黑色和白色,可以发现二分图中的每一条边都一定是连接一个黑色点和一个白色点。
定理:一张无向图是二分图,当且仅当图中不存在奇环(边数为奇数的环)
判定:我们可以用染色法进行二分图的判定,尝试用黑白两种颜色标记图中的节点:当一个节点被标记后,它的所有相邻节点应该被标记与它相反的颜色。若标记过程中产生冲突,则说明图在存在奇环。用 DFS 或 BFS 均可,多数用 DFS,时间复杂度为 \(O(N+M)\)。
【参考代码】
// cur 当前结点
// fa 父结点
// color 结点cur将被染的色
bool isBiGraph(int cur, int fa, int color) {
col[cur] = color; //给当前结点染色
for (int i = head[cur]; i; i = edge[i].next) {
int to = edge[i].to;
if (to == fa) continue;
if (col[to] == color) {
return false; // 子结点有颜色且与当前结点染色相同
}
if (col[to] == 0 && !isBiGraph(to, cur, 3-color)) {
return false; // 尝试染色失败
}
}
return true;
}
// 主函数部分
bool flag = true;
for (int i = 1; i <= n; i++) {
if (col[i] == 0) {
col[i] = 1; // 用1和2染色
if (!isBiGraph(i, 0, 1)) {
flag = false;
break;
}
}
}
if (flag) cout <<"YES" <<endl;
else cout <<"NO" <<endl;
2.1 例题1【关押罪犯】
【分析】
考虑某一个答案为ans时成立时,那么大于ans的答案也一定成立,因此答案具有单调性,可以通过二分答案解决。
设二分的答案为mid,对任意仇恨大于mid的罪犯连边,得到一张无向图,图中的节点需要划分到两个集合,且每个集合中没有边。此时,我们用染色法判定该无向图是否为二分图。根据判定结果,继续二分答案即可。
2.2 例题2【图的遍历(牛客52275)】
【题目描述】
无向图有n个点,从点1开始遍历,但是规定:按照每次“走两步”的方式来遍历整个图。可以发现按照每次走两步的方法,不一定能够遍历整个图,所以现在小sun想问你,最少加几条边,可以完整的遍历整个图。
【输入格式】
n个点,m条边,接下来是一个无向图
【数据范围】
\(n, m \le 1e5\)
【分析】
- 先不考虑走两步,只考虑要遍历整个图,那么整个图肯定是需要联通的。我们需要求出有多少个连通块,需要加的边数就是连通块个数 \(-1\),这样先保证图联通。
- 再考虑走两步的走法,可以简单画一下,如果图联通,只要存在奇环,那么就可以走完整个图,因为奇环,从环的一点走一圈后,继续走会到另一个起点,这样之前遍历的是奇数点,第二次过来就变成了偶数点,画一下就容易理解了,偶环则不行。
- 那么如果没有奇环呢?只需要在其中一个连通块中,加上一条边形成奇数环即可。
- 所以整个题等价求有多少个联通块、求是否存在奇环,可以通过 dfs ,\(O(m+n)\) 复杂度即可解决。
【参考代码】
#include <bits/stdc++.h>
using namespace std;
vector<int> e[100005];
int ans, flag = 1; // flag=1 表示不存在奇数环
int v[100005];
void dfs(int x) { // 黑白染色,同时找联通块,所以中间不能return
for (auto &it : e[x]) {
if (v[it] == -1) { // 没被染色
v[it] = v[x] ^ 1; // 相邻的点染相反的颜色
dfs(it);
} else if (v[it] == v[x]) {
flag = 0; // 相邻的点已被染色,并且颜色相同,说明有奇环
}
}
}
int main() {
int n, m;
cin >> n >> m;
for (int i = 1; i <= m; i++) {
int x, y;
cin >> x >> y;
e[x].push_back(y); // 加边
e[y].push_back(x);
}
memset(v, -1, sizeof(v));
for (int i = 1; i <= n; i++) {
if (v[i] == -1) {
ans++; // 联通块个数
v[i] = 0; // 进行染色
dfs(i);
}
}
cout << ans - 1 + flag;
return 0;
}
3 二分图的应用
3.1 二分图最大匹配(匈牙利算法)
3.1.1 一些概念
设 \(G=<V, E>\) 是二分图,\(V\)是点集,左部集合为 \(V_1\),右部集合为 \(V_2\),\(E\) 是边集,\(M\subseteq E\)。
匹配:若 \(M\) 中任何两条边没有公共点,则称 \(M\) 是 \(G\) 的一个匹配。匹配中的边称为 匹配边,反之称为 非匹配边。一个点如果属于 \(M\) 中至多一条边的端点,称为 匹配点,反之称为 非匹配点。
最大匹配:具有边数量最多的匹配称为最大匹配。
最大权匹配:当图中的边带权的时候,边权和最大的匹配为最大权匹配。
完美匹配:若 \(|V_1|=|V_2|=|M|\),则称 \(M\) 为完美匹配,也称为完备匹配。
多重匹配:给定一张包含 \(N\) 个左部结点,\(M\) 个右部结点的二分图,从中选出尽量多的边,使第 \(i(1\le i\le N)\) 个左部结点至多与 \(kl_i\) 条选出的边相连,第 \(j(1\le j\le M)\) 个右部结点至多与 \(kr_j\) 条选出的边相连,该问题被称为二分图的多重匹配,一般用 网络流 来解决。
【示例】
下图中
最大匹配:图 4 是一个最大匹配,它包含 4 条匹配边。
完美匹配:图 4 是一个完美匹配。显然,完美匹配一定是最大匹配(完美匹配的任何一个点都已经匹配,添加一条新的匹配边一定会与已有的匹配边冲突)。但并非每个图都存在完美匹配。
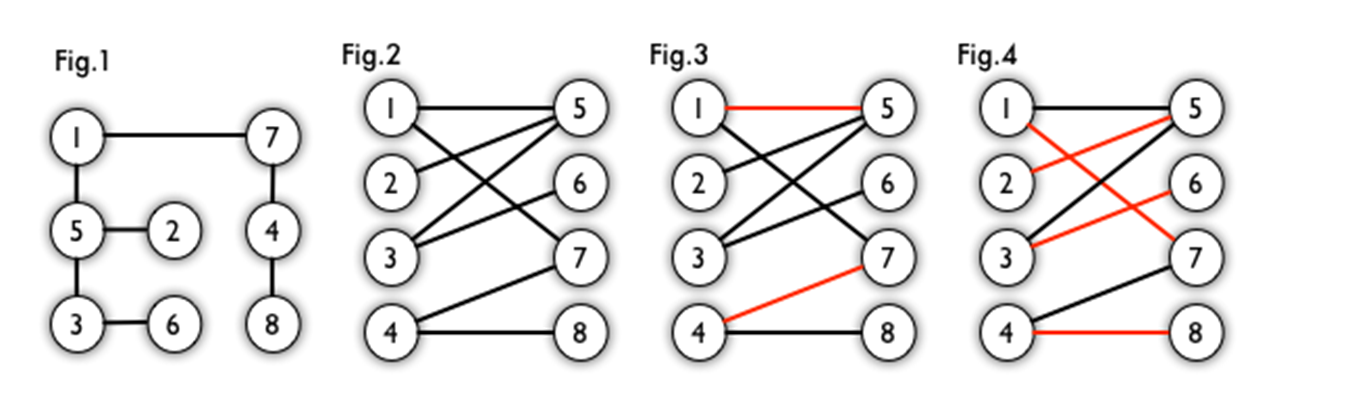
交错路:从一个未匹配的点出发,依次经过未匹配边、匹配边、未匹配边....这样的路叫做交错路。
增广路:从一个未匹配的点出发,走交错路,到达了一个未匹配过的点,这条路叫做增广路。
增广路的性质:
- 长度 \(len\) 是奇数
- 路径上第 \(1、3、5、…、len\) 条边是非匹配边,第 \(2、4、6、…、len-1\) 条边是匹配边
【示例】
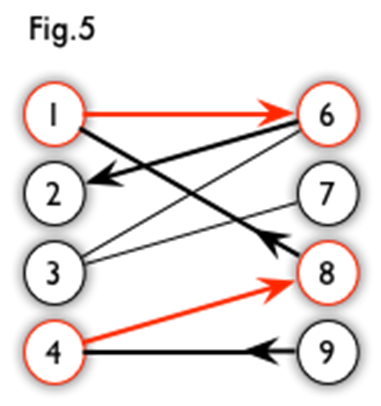
下图中,假设红色标记为我们已经找到的一个匹配,红色边表示匹配边,红色的点表示匹配点。那么从结点 9 开始,沿着图 6 的路径,可以找到一条增广路。
可以发现,我们把增广路径上的匹配边与非匹配边状态取反,便会得到一个更大的匹配。
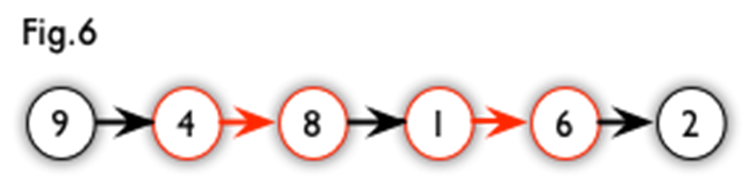
结论:二分图的一组匹配 \(M\) 是最大匹配,当且仅当图中不存在 \(M\) 的增广路。
3.1.2 匈牙利算法
求最大匹配可以看做是一个舞蹈队的人分成了两个集合,给点集1中的点从点集2中找舞伴,点集1中的点都是男的,点集2中的点都是女的,每个人都有若干个意向的舞伴。
点集1中的男的都很好说话,只要当前给他介绍的女的是单身,就同意匹配;
而且点集1中的男的还很善良,哪怕当前介绍的舞伴不是单身,只要她已经匹配的舞伴可以跟她立马分开,去匹配其他单身的舞伴,他还是可以同意匹配的。
这就是匈牙利算法的大致流程。
3.1.2.1 匈牙利算法(二分图最大匹配算法)动画模拟
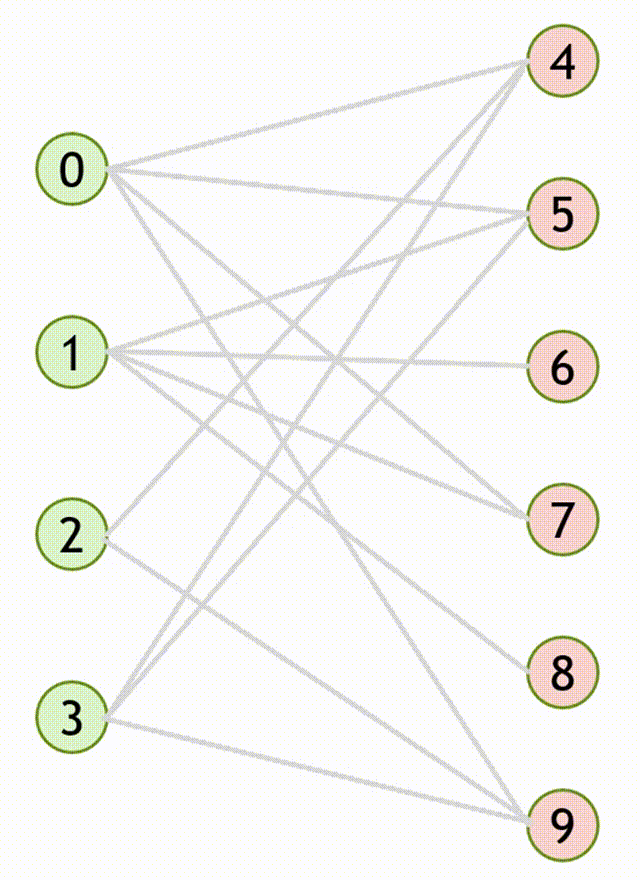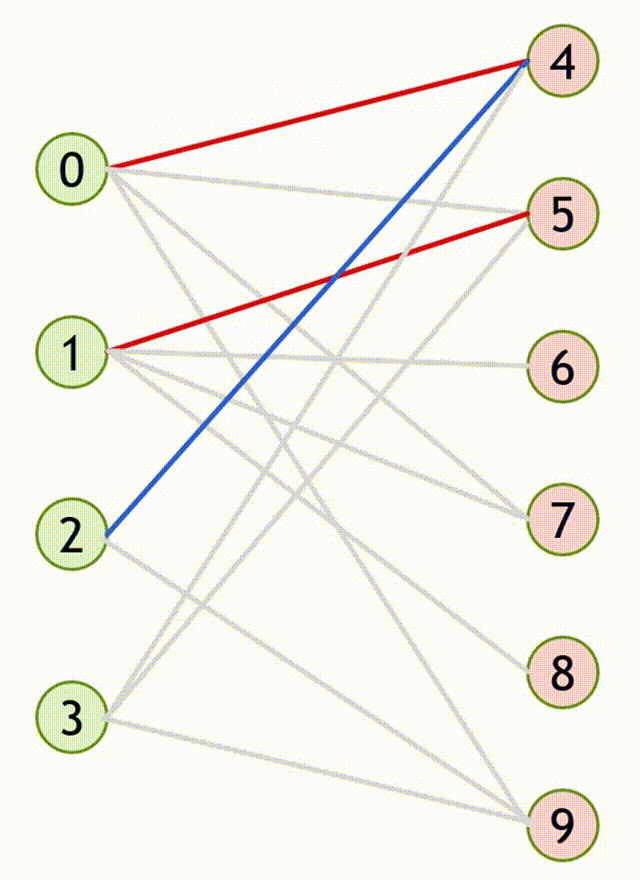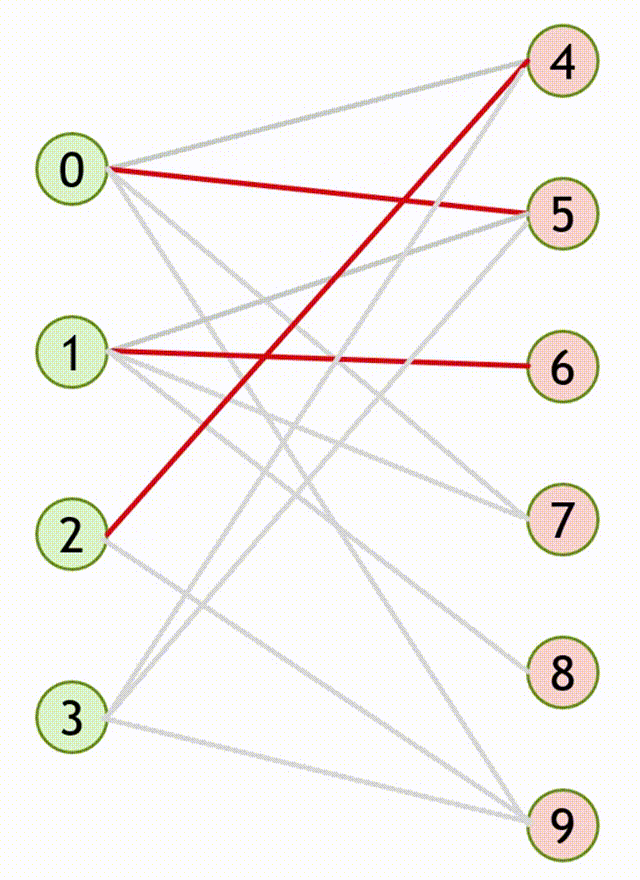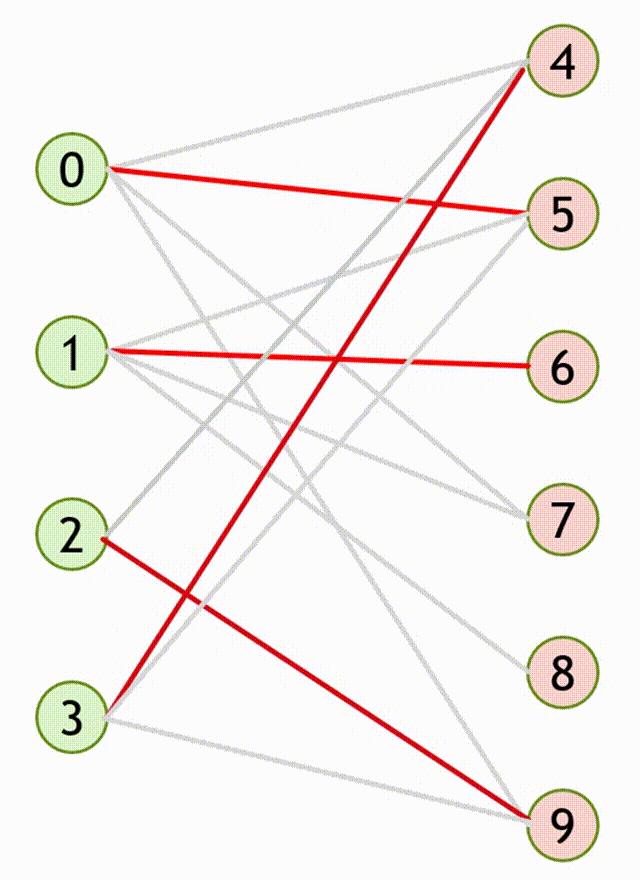
3.1.2.2 匈牙利算法流程(求二分图最大匹配算法)
- 设匹配 \(M\) 是空集,即所有边都是非匹配边
- 寻找增广路 \(path\),把路径上所有边的匹配状态取反,得到一个更大的匹配 \(M’\)
- 重复第 \(2\) 步,直至图中不存在增广路。
匈牙利算法的实现以顶点集合 \(V\) 为基础,每次左部集合中选一个顶点 \(X_i\) 做增广路径的起点搜索增广路径。搜索增广路径需要遍历边集 \(E\) 内的所有边,遍历方法可以采用深度优先遍历(DFS),也可以采用广度优先遍历(BFS),无论什么方法,其时间复杂度都是 \(O(E)\)。
匈牙利算法每个顶点 \(V_i\) 只能选择一次,因此算法的整体时间复杂度是 \(O(V*E)\)。
3.1.2.3 匈牙利算法参考代码
// 匈牙利算法求最大匹配
int xyl() {
int ans = 0; // 记录最大匹配数
for (int i = 1; i <= n; i++) {
memset(vis, 0, sizeof(vis));
// 找到一条增广路,匹配数+1
if (dfs(i)) ans++;
}
}
bool dfs(int now) {
for (int i = head[now]; i; i = edge[i].nxt) {
int to = edge[i].to;
// 这里不用考虑会有回到父结点的边的问题
// 因为每次都是从左部找邻接点
if (!vis[to]) {
vis[to] = true;
// 如果邻接点to是非匹配点,则找到一条增广路,匹配
// 如果to已匹配过,但是能重新匹配,则也找到一条增广路
// 让to与now匹配
if (!match[to] || dfs(match(to))) {
match[to] = now;
return true;
}
}
}
return false;
}
3.1.3 例题
3.1.3.1 例 1【文理分班】
【题目描述】
\(jzyz\) 每年的文理分班的时候,每个班都会有一些同学分到其他班,还会进入一些其他班的同学进入这个班。
小 \(x\) 负责安排座位,为了照顾分班带来的那种伤感情绪,小 \(x\) 制定了很人性化的座位安排计划,具体计划如下:
比如 \(A\) 和 \(B\) 都是本班学生且是好朋友,\(A\) 分到了其他班,而 \(C\) 则是外班进入这个班的,\(C\) 和 \(A\) 并不熟悉,而 \(C\) 和 \(B\) 关系很好,那么小 \(x\) 为了照顾 \(A\) 和 \(C\) 的情绪,就会让 \(B\) 坐在 \(A\) 的位置,\(C\) 坐在 \(B\) 的位置。
当然,实际情况可能很复杂,比如一个班里的同学之间关系不一定好,外班进来的可能和本班很多人关系都很好。
现在告诉你,和小 \(x\) 所在班有关系的人一共有 \(n\) 个人,小 \(x\) 想知道有没有一个合理的方案来满足自己的座位安排计划。
【输入格式】
本题为多组数据,第一行一个整数 \(M\),表示有 \(M\) 组测试数据。
对于每组测试数据,每组的第一行一个整数 \(n\),表示一共有 \(n\) 个人和这个班有关系。
接下来一行 \(n\) 个整数,第i个整数表示第 \(i\) 个人是否是本班学生(\(0\) 表示不是,\(1\) 表示是,分到其他班的也算是本班学生)
接下来一行 \(n\) 个整数,第 \(i\) 个整数表示第 \(i\) 个人是否要分到其他班(\(0\) 表示留在本班,\(1\) 表示分到其他班,如果第 \(i\) 个人是由外班分进来的,那么第 \(i\) 个整数就是一个随机整数,没有实际意义)
接下来是一个 \(n\) 行 \(n\) 列的一个二维矩阵,第 \(i\) 行第 \(j\) 列的数表示第 \(i\) 个人和第 \(j\) 个人是否关系很好(\(1\) 表示认识,\(0\) 表示不认识),对角线上是 \(0\),但是自己肯定认识自己。
【输出格式】
每组数据,如果存在一个方案,输出 “_”(不含引号)。
如果没有方案,输出 “T_T”(不含引号)。都是半角字符。
【数据范围】
\(1 ≤ n ≤ 50,1 ≤ T ≤ 20\)。
【分析】
题目大意是根据学生之间的认识关系,考虑换座位是否冲突。因为只需要考虑本班安排座位的问题,所以原来不是本班的学生一定会来,调走的学生不用管。
如果 \(A\) 认识 \(B\),则不管 \(A\) 是本班还是外来,都可以坐在 \(B\) 的位置。
如果某个学生 \(x\) 是本班学生且留在本班,可以认为他自己跟自己换,避免跑匈牙利算法的时候,出现该点无法匹配而判错的情况。但是,外来学生不能自己跟自己换位。
根据可换位的关系,我们构建一张图,跑匈牙利算法,如果发现有匹配不了的,则失败;否则成功。
建图
对于结点 \(i\):
- 如果 \(i\) 被分到其他班,则不用管;
- 如果 \(i\) 是本班学生且留在本班,则自己可以换到自己的座位;
- 对于结点 \(i\) 和 \(j\),如果 \(i\) 认识 \(j\),且 \(j\) 原来是本班的,\(i\) 到 \(j\) 连边,表示 \(i\) 可以坐到 \(j\) 的位置(如果 \(j\) 是外来的,即使 \(i\) 认识 \(j\) 也没法换位,因为 \(j\) 原本没有位置)。
判断
对没有被分出去的结点跑匈牙利,只要每个节点都能正常匹配即可;否则只要有一个不能匹配则失败。
【参考代码】
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int maxn = 1050;
int n, k, m, vis[maxn], match[maxn], ans, g[maxn][maxn], a[maxn], b[maxn];
int find(int u) { //匈牙利
for (int i = 1; i <= n; i++) {
if (g[u][i] && !vis[i]) {
vis[i] = 1;
if (!match[i] || find(match[i])) {
match[i] = u;
return 1;
}
}
}
return 0;
}
int main() {
scanf("%d", &m);
while (m--) {
memset(g, 0, sizeof(g));
memset(match, 0, sizeof(match)); //多组测试,记得初始化
scanf("%d", &n);
for (int i = 1; i <= n; i++) scanf("%d", &a[i]); //是否为本班学生
for (int i = 1; i <= n; i++) {
scanf("%d", &b[i]); //是否分走
if (a[i] == 1 && b[i] == 0) g[i][i] = 1; //是本班学生且没被分走,自己可以和自己换坐
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
int x; scanf("%d", &x);
if (a[i] && b[i]) continue; // 本班学生分走,不用管
if (x == 1 && a[j] == 1) g[i][j] = 1; //i和j很熟, 且j是本班的(即使j被分到外班,j的座位还在本班)
}
}
bool flag = 0;
for (int i = 1; i <= n; i++) {
memset(vis, 0, sizeof(vis));
if ((!a[i]) || (a[i] && !b[i])) { //i不是本班学生(外班来的)或i是没有被分走的本班学生
if (!find(i)) {//找不到可以换坐的人
flag = 1;
break;
}
}
}
printf("%s\n", flag ? "T_T" : "^_^");
}
return 0;
}
3.1.3.2 例 2 【P2825 [HEOI2016/TJOI2016] 游戏】
【题目描述】
在 2016 年,佳媛姐姐喜欢上了一款游戏,叫做泡泡堂。
简单的说,这个游戏就是在一张地图上放上若干个炸弹,看是否能炸到对手,或者躲开对手的炸弹。在玩游戏的过程中,小 H 想到了这样一个问题:当给定一张地图,在这张地图上最多能放上多少个炸弹能使得任意两个炸弹之间不会互相炸到。炸弹能炸到的范围是该炸弹所在的一行和一列,炸弹的威力可以穿透软石头,但是不能穿透硬石头。
给定一张 $ n \times m $ 的网格地图:其中 * 代表空地,炸弹的威力可以穿透,可以在空地上放置一枚炸弹。 x 代表软石头,炸弹的威力可以穿透,不能在此放置炸弹。# 代表硬石头,炸弹的威力是不能穿透的,不能在此放置炸弹。例如:给出 $ 1 \times 4 $ 的网格地图 *xx*,这个地图上最多只能放置一个炸弹。给出另一个$ 1 \times 4 $ 的网格地图 *x#*,这个地图最多能放置两个炸弹。
现在小 H 任意给出一张 \(n \times m\) 的网格地图,问你最多能放置多少炸弹。
【输入格式】
第一行输入两个正整数 \(n, m\),\(n\) 表示地图的行数,\(m\) 表示地图的列数。
接下来输入 $ n $ 行 $ m $ 列个字符,代表网格地图。*的个数不超过 $ n \times m $ 个。
【输出格式】
输出一个整数 $ a $,表示最多能放置炸弹的个数。
【样例输入 】
4 4
#***
*#**
**#*
xxx#
【样例输出】
5
【数据范围】
\(1 \leq n,m \leq 50\)
【分析】
首先观察一下题目,若是把硬石子全部当成软石子,就可以将题意转换成:“每摆放一个炸弹,它所在的行和列都不再能摆放其它的棋子,其中本身就有一些点是不可以摆放炸弹的。”是不是很简单?
将行看成集合 \(S\),将列看成集合 \(T\) (两个集合内部无连边,即不同行的炸弹在行方向上互不影响,不同列的炸弹在列方向上互不影响),再将每个可以放置炸弹的点,从行 \(x\) 向列 \(y\) 建边,此时每条边表示可以在 \((x,y)\) 位置放炸弹。
那么能够摆放的炸弹的个数就是 \(S\) 与 \(T\) 的最大匹配,这是一个经典的二分图最大匹配应用题。
加了硬石子,又怎么做?
如果一行内存在一个硬石子,这一行就会被分成不相邻的两部分。如果把这两部分都分别看成两个独立的行,此时,不同行的炸弹在行方向上仍然互不影响,列与行仍然会相交,依旧满足二分图的性质,此方案可行。
拿样例举个例子:
#***
*#**
**#*
xxx#
如果将硬石子看成软石子,分别对每行可以放炸弹的位置做行方向的编号,原来的矩阵长如下:
#111
2#22
33#3
xxx#
但是硬石子将每行划分成了多个单独的行,因此我们要将硬石子后的可放石子的节点所处的行加一。
注意:这里的行已经不是原来意义上的行了,这里是被硬石子分割后的逻辑意义的行
#111
2#33
44#5
xxx#
这样,我们就把行的编号处理完了,列的编号也同理。
我们已经得到每个可以放置炸弹的点所对应的行号 \(x\) 与列号 \(y\),此时遍历所有点,将 \(x\) 与 \(y\) 建有向边(无需反向建边),最后求最大匹配即可。
【参考代码】
#include <bits/stdc++.h>
using namespace std;
int n, m, ntot, mtot, tot, head[3000], nxt[3000], to[3000], row[60][60], col[60][60], match[3000], ans;
bool vis[3000];
void add(int x, int y) {// 链式前向星加边
to[++tot] = y;
nxt[tot] = head[x];
head[x] = tot;
}
bool find(int x) {// 匈牙利算法
for (int i = head[x]; i; i = nxt[i]) {
int y = to[i];
if (!vis[y]) {
vis[y] = true;
if (!match[y] || find(match[y])) {
match[y] = x;
return true;
}
}
}
return false;
}
int main() {
scanf("%d%d", &n, &m);
char s[60][60];
bool flag = 1; // 注意第一次需要单开一行
pair<int, int> last; // 与动态规划的思想相似,每个点所在的逻辑的行的编号都可以由上一个有编号的点转移过来
for (int i = 1; i <= n; i++) {
scanf("%s", s[i] + 1);
for (int j = 1; j <= m; j++) {
if (s[i][j] == '#') { // 硬石头,要另开一行(逻辑意义上的行)
flag = 1;
continue;
}
if (flag == 0) { // 未出现硬石头,也未换行,不需要加1
if (s[i][j] != 'x') // 此位置可放炸弹
{
row[i][j] = row[last.first][last.second]; // row数组的意义为该点所在的逻辑的行编号
last = make_pair(i, j);
}
}
else // 出现过硬石头或换行
{
if (s[i][j] != 'x') {
row[i][j] = row[last.first][last.second] + 1; // 逻辑的行编号要加 1
ntot++; // 更新总的逻辑行数
last = make_pair(i, j);
flag = 0; // 当前的加处理完毕,恢复状态
}
}
}
flag = 1; // 换行一定要加 1
}
// 下面是列的处理,与行相似,但是i与j相反
flag = 1;
last = make_pair(0, 0); // 清零,赋初值
// 编号部分代码略去,自己完成
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= m; ++j) {
if (s[i][j] == '*')
add(row[i][j], col[i][j]); // 加边
}
for (int i = 1; i <= ntot; ++i) {
memset(vis, 0, sizeof(vis));
if (find(i))
ans++; // 统计最大匹配
}
printf("%d\n", ans);
return 0;
}
3.1.4 相关结论
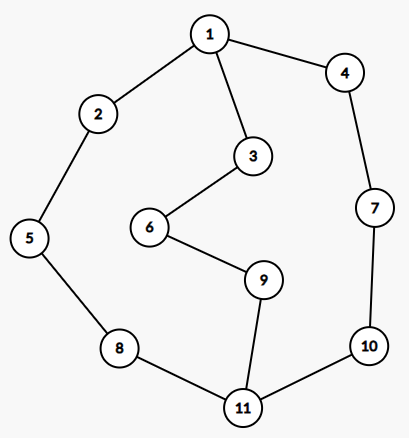
顶点覆盖
对于图 \(G=(V,E)\),选取顶点集合 \(V\) 的子集 \(V'\subseteq V\),使得 \(\forall e\in E\),至少有一个端点在 \(V'\) 中。
最小顶点覆盖
在所有的顶点覆盖集中,顶点数最小的称为最小顶点覆盖。
二分图中最小点覆盖数=最大匹配数
上图中最小点覆盖大小为 \(5\)。
独立集
对于图 \(G=(V,E)\),选取顶点集合 \(V\) 的子集 \(V'\subseteq V\),使得其中任意两个顶点之间没有连边。
最大独立集
在所有的独立集中,顶点数最多的集合称为最大独立集。
二分图中最大独立集数=n-最小点覆盖数
上图中最大独立集大小为 \(6\)
3.2 二分图最大权完美匹配(KM 算法)
给定一张二分图,二分图的每条边都带有一个权值。求出该二分图的一组最大匹配,使得匹配边的权值总和最大。该问题称为二分图的带权最大匹配,也称二分图的最优匹配。
其中,二分图最大权完美匹配是指给定二分图 \(G=(V,E)\),若边集 \(M\subseteq E\) 满足 \(M\) 中任意两条边不交于同一端点,\(|M|=|V_1|=|V_2|\) 且 \(M\) 的边权和最大,则称 \(M\) 是 \(G\) 的一组最大权完美匹配。将 \(|M|=|V_1|=|V_2|\) 这个限制去掉,则称 \(M\) 是 \(G\) 的一组最大权匹配。
最大权匹配不一定是最大权完美匹配,如下图,最大权匹配是 \(20\),最大权完美匹配是 \(3\)。
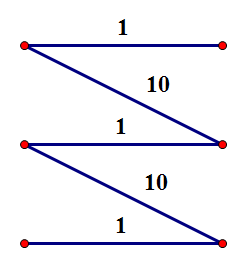
\(KM\) 算法用于求解二分图最大权 完美 匹配
考虑到二分图中两个集合中的点并不总是相同,为了能应用 KM 算法解决二分图的最大权匹配,需要先作如下处理:
- 将两个集合中点数比较少的补点,使得两边点数相同,再将不存在的边权重设为 \(0\),这种情况下,问题就转换成求 最大权完美匹配问题,从而能应用 KM 算法求解。
3.2.1 一些概念
顶标
也叫做“顶点标记值”。在二分图中,我们定义 \(w(i,j)\) 表示左部第 \(i\) 个结点和右部第 \(j\) 个结点的边权。给左部的每个结点一个权值 \(L_i\),右部的每个结点一个权值 \(R_j\),同时满足:对 \(\forall i, j\),有 \(L_i+R_j\ge w(i,j)\)。这里的 \(L_i、 R_j\) 称为结点的顶标。
相等子图
二分图所有结点与满足 \(L_i+R_j=w(i,j)\) 的边构成的子图,称为二分图的相等子图。
交错树
从未匹配点 \(x\) 进行 DFS 或 BFS 寻找增广路的过程中产生的树称为交错树,\(x\) 是交错树的根。设 \(T=(V_t,E_t)\) 为寻找增广路时产生的交错树。定义:
- 偶点(黑点)为树上深度为偶数的点。
- 奇点(白点)为树上深度为奇数的点。
下图展示了一个二分图和从未匹配点 \(1\) 开始寻找增广路时,形成的以 \(1\) 为根的交错树。
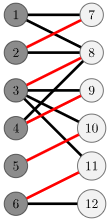
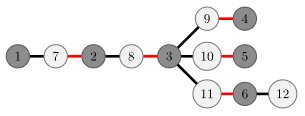
【定理】
若相等子图存在完备匹配,则这个完备匹配就是二分图的带权最大完美匹配。
【证明】
在相等子图中,完备匹配的边权之和为 \(\sum_{i=1}(L_i+R_i)\),即所有顶标这和。
因为顶标满足:对 \(\forall i, j\),有 \(L_i+R_j\ge w(i,j)\),所以在整个二分图中,任何一组匹配的边权之和都不可能大于所有顶标的和。
3.2.2 KM 算法基本思想
-
初始化可行顶标
顶标要满足:对 \(\forall i, j\),有 \(L_i+b_j\ge w(i,j)\),一般我们可以初始化 \(L_i=max_{1\le j\le N}\{w(i,j)\},\,R_j=0\) -
设当前希望处理的结点为 \(x\),则从 \(x\) 开始搜索。搜索前清空右部点之前的访问标记,以及右部点的 \(slack_y\),它表示 \(min{A_x+B_y-w_{x,y}}\),即每次找增广路失败时,需要调整的值,初始化为 \(+\infty\)。
-
遍历 \(x\) 所有的出边对应的右部的点 \(y\):
- 若 \(y\) 已被访问过,则跳过
- 若 \(A_x+B_y=w_{x,y}\),则 \((x, y)\) 在相等子图上。此时找增广路(若 \(y\) 是非匹配点或递归 \(y\) 对应的左部点 \(x'\) 时能成功增广),若成功增广,则返回成功信息,否则,换下一条边尝试。
- 若边 \((x,y)\) 不在相等子图上,用 \(A_x+B_y-w_{x,y}\) 更新 \(slack_y\)。
-
\(x\) 搜索完毕后
- 若成功增广,结束 \(x\) 的增广,继续下一个结点。
- 若未能成功增广,说明从 \(x\) 出发无法增广。此时所有遍历过的点在一棵交错树上,需要将树上所有点的顶标进行调整。令 \(d\) 为所有未匹配的右部点 \(y\) 的 \(min{slack_y}\)。让所有被访问的左部点的顶标减少 \(d\),已匹配的右部点的顶标增加 \(d\)。重新从 \(x\) 找增广路,直到找到一条增广路为止。
时间复杂度约为 \(O(n^4)\),可以应付大部分题目。
3.2.3 KM 算法流程参考
https://blog.csdn.net/lemonxiaoxiao/article/details/108704280
KM 算法参考代码
//邻接矩阵存图,A B分别代表左右部的顶标
//slack记录每次顶标的调整值
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
constexpr int N = 500 + 5;
ll e[N][N], A[N], B[N], slack[N];
int n, m, mch[N], vis[N];
//匈牙利算法找增广路,如果成功找到增广路,则返回 1
//否则,更新顶标调整值,访问过的点都是交错树上的点
//需要调整顶标的值
bool dfs(int id) {
for (int it = 1; it <= n; it++) {
if (vis[it]) continue;
if (A[id] + B[it] == e[id][it]) { //相等子图的一条边
vis[it] = 1;
if (!mch[it] || dfs(mch[it])) return mch[it] = id, 1;
}
else { //更新顶标调整值
slack[it] = min(slack[it], A[id] + B[it] - e[id][it]);
}
}
return 0;
}
int main() {
cin >> n >> m;
memset(e, 0xcf, sizeof(e));
for (int i = 1; i <= m; i++) {
int y, c, h;
cin >> y >> c >> h;
e[y][c] = h;
}
memset(A, 0xcf, sizeof(A));
//左部顶标初始化为该点出边的最大边权,右部为0
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
A[i] = max(A[i], e[i][j]);
//匈牙利算法
for (int i = 1; i <= n; i++) {
while (1) {
//注意初始化的位置
memset(vis, 0, sizeof(vis)); //只标记右部的点,左部访问过的点可以通过右部点的匹配记录得到
memset(slack, 0x3f, sizeof(slack));
if (dfs(i)) break; //成功找到增广路,换下一个结点
//匹配失败,调整上面搜索的交错树上结点的顶标值
ll d = 1e18;
for (int j = 1; j <= n; j++) if (!vis[j]) d = min(d, slack[j]);
for (int j = 1; j <= n; j++) if (vis[j]) B[j] += d, A[mch[j]] -= d;
A[i] -= d; //注意递归起点的顶标值修改
}
}
ll ans = 0;
for (int i = 1; i <= n; i++) ans += A[i] + B[i];
cout << ans << "\n";
for (int i = 1; i <= n; i++) cout << mch[i] << " ";
cout << "\n";
return 0;
}
3.2.4 例题
HDU2255
浴谷P6577


