三傅里叶变换
1 傅里叶变换
研究同一个事物,在不同的领域的视角是怎么不同的
傅里叶变换和逆变换是无损的
3 变换的目的
有的操作在不同的领域的成本不同

上面的音频:可以由傅里叶转换为下面

这样就可以将音频拆分为男女不同的音频
4 图上做变换的必要性
图具有任意复杂的拓扑结构,无法给一个特定形状的卷积核的,每个点的邻居数量是未知的
因此,在空间域,做图的卷积是很困难的
5 图上的傅里叶变换
LX(L见上骗博客)
X是n行的列向量,每个节点都有一个值作为feature
LX:N*1的向量,第一维是(x1-和x1相连的节点的feature)之和
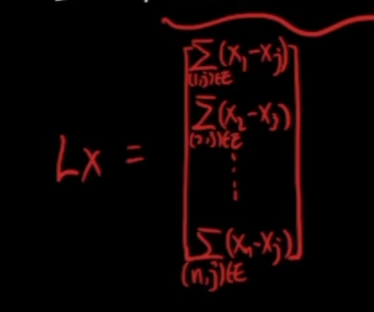
其实是做了一次邻居的聚合,也是卷积的本质
L是实对称,半正定的矩阵,L可以分解为:
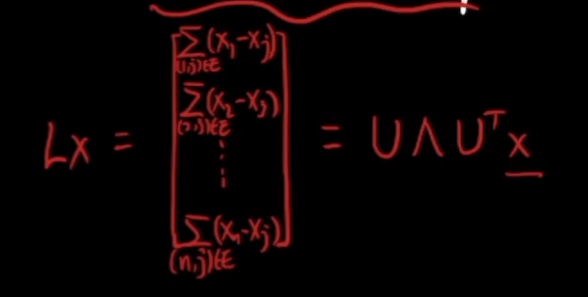
U是正交矩阵,UT也是正交阵。
UTX就是让x变换一下基底 空间系的基底变换,去了一个新的域(UTx)
在新的域,对每一个维度做一个放缩,实现聚合邻居的目的(尖的作用)
再用逆变换变换回去(U就是逆变换)
6 难点
特征值分解,求矩阵的拉普拉斯矩阵L的复杂度是为o(n*n)
小规模矩阵尚可以接受,现实庞大数据不可能
GCN对傅里叶变换做了限制,推到了一种不需要带特征值分解,复杂度和边的数量成线性关系的方法


 浙公网安备 33010602011771号
浙公网安备 33010602011771号