算法工程师的升级之路-数据结构与算法篇(2)归并排序

引言

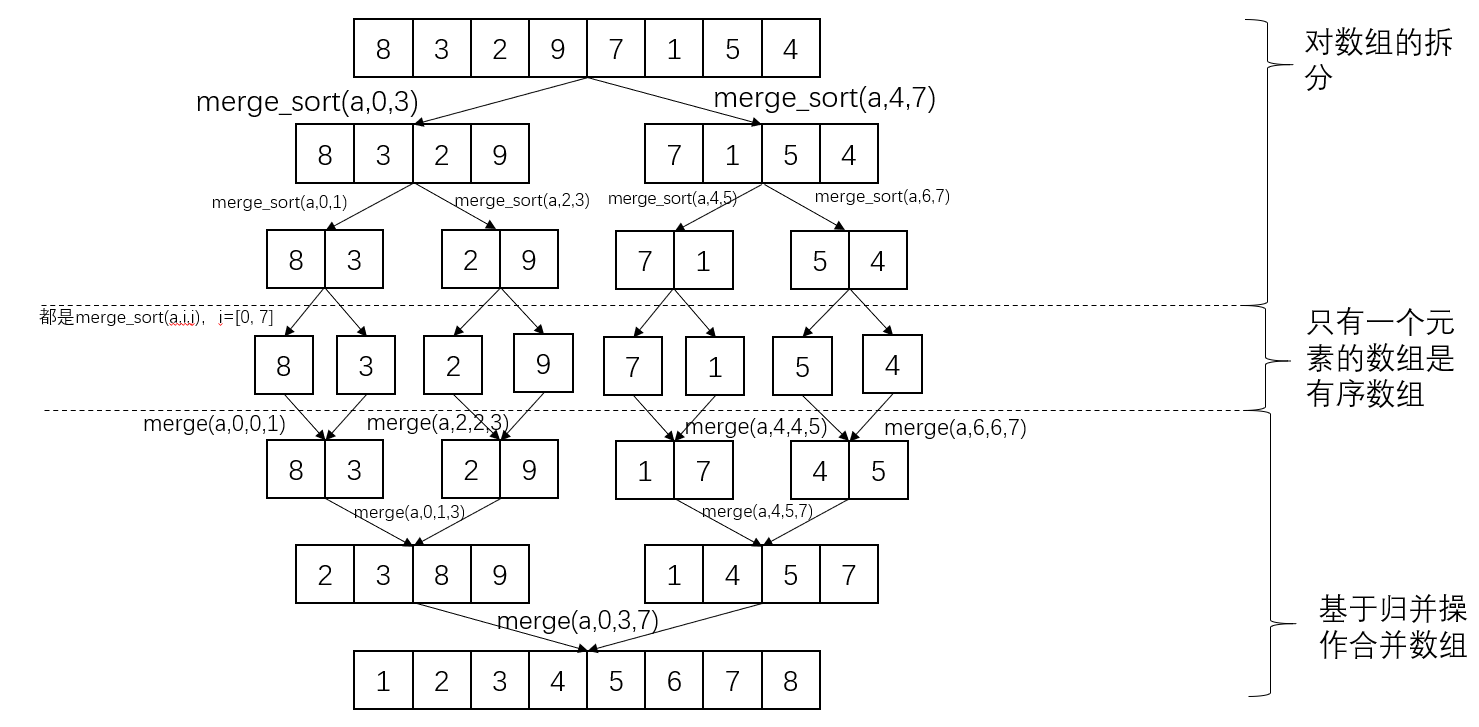
　　本次将要介绍归并排序算法，归并排序是分治算法的一个很典型的例子，将排序问题递归地拆分为子数组的排序问题(分)，然后逐个攻破，通过归并操作将排序好的数组进行合并。

归并操作

　　归并操作是归并算法的核心步骤，归并算法的输入是两个排序好的子数组，返回一个合并的排序好的数组。

　　为了方便实现，以下归并操作是借助辅助数组的C++实现

void merge(std::vector<int> &a, int lo, int mid, int hi)
{//合并两个有序子数组为一个有序数组a[lo, ..., mid]+a[mid+1, ..., hi] ---> a[lo, ..., hi]
    int i=lo,j=mid+1;                               //两个子数组的指针
    std::vector<int> aux(a.size(),0);               //辅助数组
    for(int k=lo;k<=hi;k++) aux[k]=a[k];
    for(int k=lo;k<=hi;k++)
    {
        if(i>mid)               a[k]=aux[j++];      //第一个数组的索引有效范围是i：[lo, ..., mid], 当i>mid说明第一个子数组的元素已经被取完了，故取第二个子数组的元素
        else if(j>hi)           a[k]=aux[i++];      //同理，第二个数组元素被取完
        else if(aux[j]<aux[i])  a[k]=aux[j++];      //两个数组都没被取完，则将比较小的元素放到合并后的数组前面
        else                    a[k]=aux[i++];      //逻辑同上
    }
}

　下面结合图像来理解归并操作的原理。上面两个分离的子数组为aux，为了方便区分，没有将它们画到一个数组里，实际上这两个子数组是通过索引的范围来确定的；下面的数组为a。蓝色代表已经放置在正确位置上的元素。

 

 

 

 

 

 

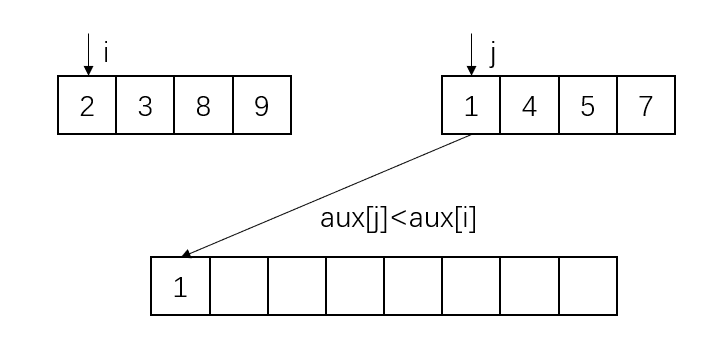
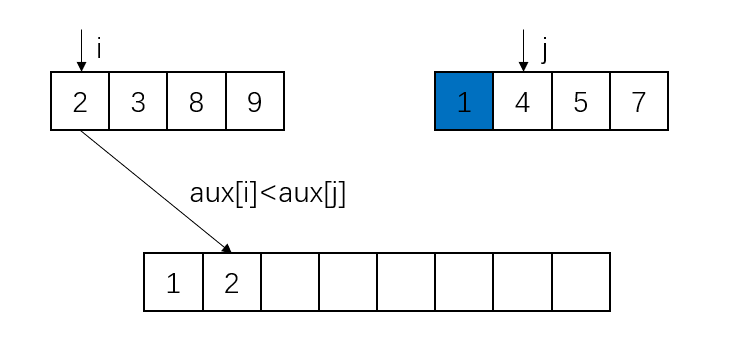
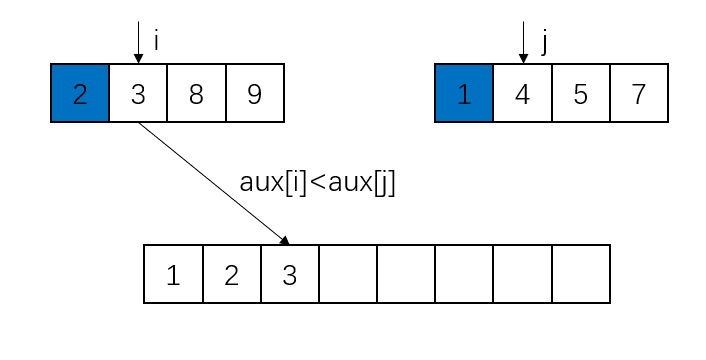
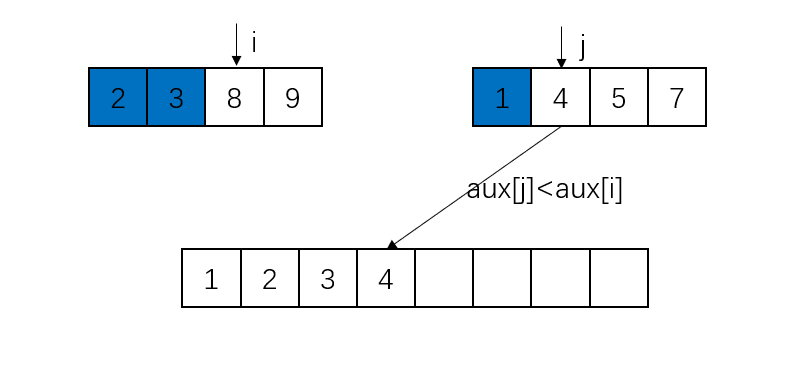
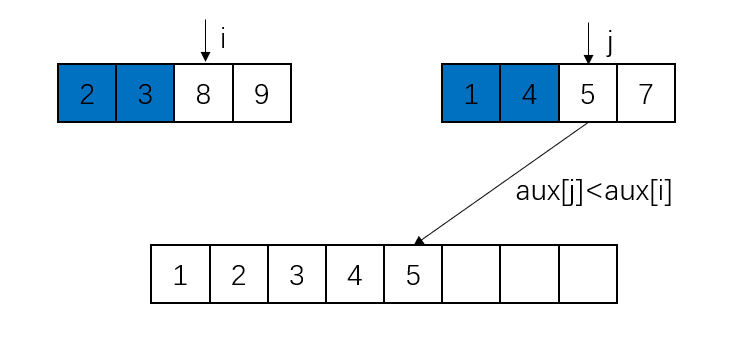
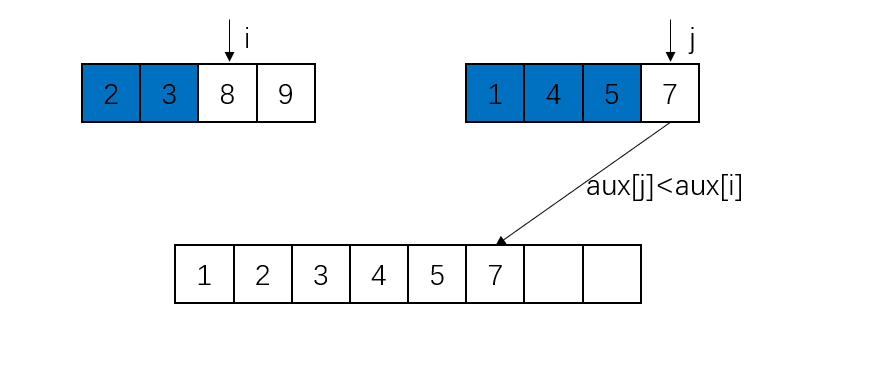
　　此处第二个子数组的元素被取完，所以直接将第一个子数组的元素放置到数组a的对应位置即可。

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

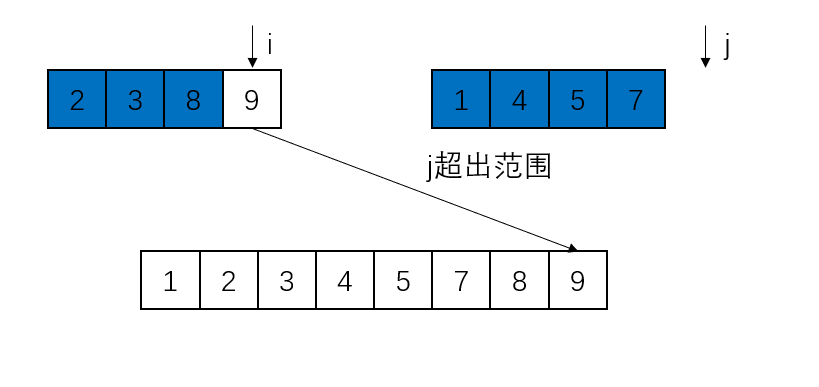
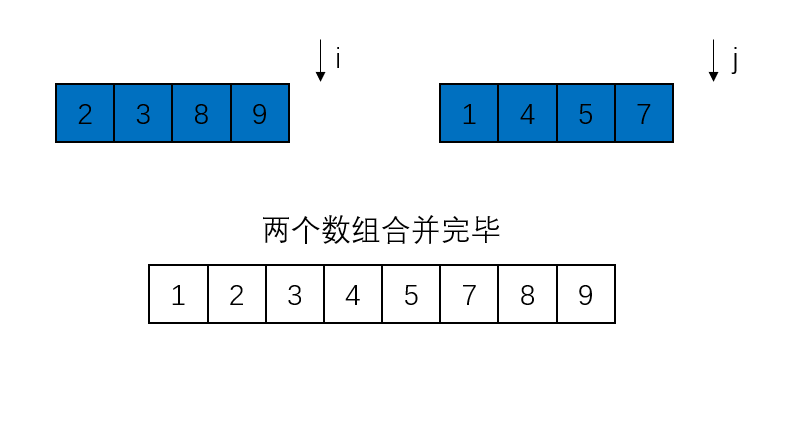
递归排序

　　归并操作十分地简单且直接，真正让归并排序发挥出威力的是分的操作。此处借助递归和归并操作，实现自顶向下的归并排序。

void merge_sort(std::vector<int> &a, int lo, int hi)
{//使用归并排序对数组a[lo, ..., hi]进行排序
    if(lo>=hi) return;              //数组不多于1个元素，已经有序
    int mid = lo+(hi-lo)/2;         //这里是为了避免相加结果溢出
    merge_sort(a, lo, mid);         //对切分的子数组排序
    merge_sort(a, mid+1, hi);
    merge(a, lo, mid, hi);          //对切分后有序的两个子数组进行合并操作
}

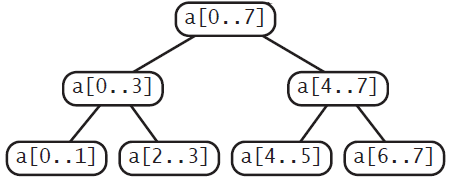
　　下面为了理解归并排序，绘制函数的递归调用树。

 

　　 从代码实现来看，可以发现这种递归形式与二叉树的后续遍历是一样的形式，下面以长度为4的数组为例

merge_sort(a,0,3)
    merge_sort(a,0,1)
    |   merge_sort(a,0,0)
    |   merge_sort(a,1,1)
    |   merge(a,0,0,1)
    merge_sort(a,2,3)
    |   merge_sort(a,2,2)
    |   merge_sort(a,3,3)
    |   merge(a,2,2,3)
    merge(a,0,1,3)

 时空复杂度分析

 　　首先进行简单的分析，经过上面的分析，以长度为8的数组为例，函数调用的递归树如下图

 

 　　可以发现归并函数的递归树为满二叉树，结点的每一次分裂都是数组长度减半，所以递归树高度为log n。每一次分割对应一次归并操作，归并操作的时间复杂度为O(n)。所以对于归并排序算法的时间复杂度为O(n logn)。

　　通过列归并排序算法的时间复杂度递推关系式，又递归代码可知，归并排序将数组排序分解为大小减半的两个子数组的归并排序和一个归并操作，其中归并操作的时间复杂度为线性时间复杂度，得到T(n)=2T(n/2)+O(n)。

　　根据主定理，当T(n)=aT(n/b)+f(n)，f(n)=O(n^d)时

　　①T(n)=O(n^d)， 当a<b^d时

　　②T(n)=O(n^dlog n)， 当a=b^d时

　　③T(n)=O(n^log_ba)， 当a>b^d时

　　由已知条件，属于情况②，所以得到时间复杂度为O(n logn)。

　　对于空间复杂度，借助辅助数组的归并排序算法是线性空间复杂度的O(n)。同时还有inplace版本的归并排序算法实现，所以空间复杂度为O(1)，有兴趣的同学可以自己去看看。

 

 

 

 总结

　　本次我们学习了归并排序的基本思想和简单自顶向下的的算法代码实现，归并排序算法是一个很经典的分治算法的例子，将问题进行分解的思路在日常生活中也是很实用的思想。推荐大家在学习时结合图像进行思考，充分调动左右脑，这里是一个关于归并算法的一个可视化(https://www.cs.usfca.edu/~galles/visualization/ComparisonSort.html)