算法工程师的升级之路-数据结构与算法篇(1)堆排序
引言
在学习堆排序前,需要简要了解选择排序的原理。因为堆排序的本质是一种使用了特殊数据结构的选择排序。
选择排序的伪代码如下:
SelectionSort(A):
for i=1 to n:
找到A的最小元,并赋值给Sort[i]
删除A的最小元
return Sort
在for循环里面的每一次寻找最小元的过程都是O(n)的时间复杂度,所以选择排序算法的时间复杂度是O(n^2)的。所以针对找到最小元的操作,将它进行简化就可以有效地减小时间复杂度。
堆排序的思想介绍
为了实现快速找到最小元,借助一种名为堆的数据结构。堆是一种非严格有序的数据结构,这种结构保证了它能提供高效的取最小元操作。
下面以大顶堆为例子进行堆的介绍。
在介绍堆之前,先简要地介绍完全二叉树的概念,完全二叉树指的是处理最后一层外,其余层的结点是满的,且最后一层结点优先放置在最左边。如图1所示
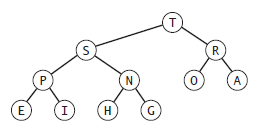
图1.完全二叉树
完全二叉树的优点是,它能够在空间浪费小的情况下使用数组表示一个完全二叉树。对于有N个结点的完全二叉树,使用N+1大小的数组表示,数组的第一个位置(位置0)不放置元素,位置k的结点的两个子结点位置分别为2k和2k+1,父结点的位置为k/2向下取整。所以可以很简单地通过数组的索引进在树中上下移动。
完全二叉树的示意图如图2所示
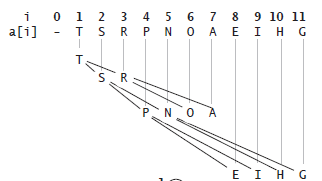
图2.完全二叉树数组表示法
堆是一课保持上下有序性的完全二叉树,上下有序性指的是:堆的每个结点都大于或等于它的左右子节点。而这种有序性确保了最上层的根结点是整个堆最大的元素,所以单纯的取堆顶元素就是常数时间的操作,从而实现了前面想要的高效取最小元的操作。但是这是要付出代价的,取走堆顶元素后的,一个堆就变成两个堆了,如此进行下去取最大元的操作耗费的时间就会越来越多,退化为线性时间的查找。所以为了更好地使用堆的高效取最大元的性质,需要对取走最大元后的堆进行一定的操作(一时的不白嫖是为了更好地白嫖,白嫖一时爽,一直白嫖一直爽)
为了保持取走堆顶最大元素后仍能维持一个堆的性质,将堆最末尾的元素(即数组的最末尾元素)移动到堆顶,然后根据堆的性质,对比当前的堆顶元素和它的左右结点,重新维护堆的性质,因为是堆尾移动来的,大概率不满足堆的性质,所以需要将堆重新排列,以让其重新满足堆的性质。此处需要的操作称为形象地称为下沉,将堆顶元素与左右结点进行大小比较,将最大的元素对应结点与堆顶元素进行交换,实现了新元素从第一层下沉到第二层。以此类推,到达第二层的相应位置继续执行与左右结点的下沉,从而实现取走堆顶元素后的堆的维护。下沉操作是以层级间的元素交换为基础的,所以下沉操作需要执行的次数与堆的高度是相关的,而由于堆是完全二叉树,所以对于含有n个结点的堆,它的高度是log(n),所以对于堆的维护是O(log n)时间复杂度的操作。将取最大元和堆的重新维护看着是一个操作,堆的取最大元操作时间复杂度是O(log n)级别的。
所以,很显然,以堆为数据结构的选择排序在循环中的取最小元操作,通过小顶堆可以在O(log n)的时间复杂度内完成,结合外层的O(n)循环,(基于)堆排序的时间复杂度为O(n*logn)。
上面就是堆排序的基本思路,不同于一般的二叉树,完全二叉树可以通过数组进行实现,且不会造成空间的浪费。
堆排序的整体思路就是介绍完毕,为了更好地理解对排序,我们需要结合代码进行理解。
堆排序的代码实现
在对堆排序的原理进行讲解的时候,使用到最多的操作是交换元素和下沉操作。所以首先实现这两个操作。
void exch(vector<int>&a,int i,int j)//交换
{
int temp=a[i];
a[i]=a[j];
a[j]=temp;
}
void sink(vector<int>&a, int k, int N)
{
while(2*k<=N)
{
int j=2*k;//左边子结点的索引
if(j<N&&a[j]<a[j+1])j++;//定位子结点中的较大值
if(a[k]>=a[j])break;//若已经满足堆的性质,则跳出循环
exch(a,k,j);//否则将三个结点中最大的元素放到堆顶
k=j;//根据堆的上下有序性,因为交换前元素位于子堆的最大位置,所以交换后元素k有可能比堆的子结点更小,需要继续下沉
}
}
堆排序可分为两个阶段:构建堆和取走最大元。
构建堆的方法可以很简单,通过逐个添加元素到数组尾部,然后维护堆的性质即可,这种实现的时间复杂度为O(n logn)。一种更快的构建方法是从数组中间进行构建,跳过大小为1的子堆。
void bulid(vector<int> &a)
{
int N=a.size()-1;//实际上位置0的元素是不使用的
for(int k=N/2;k>=1;k--)
sink(a,k,N);
}
构建好堆后,获取堆顶的最大元素并删除,递归执行直至数组有序。
void sort(vector<int> &a)
{
bulid(a);
int N=a.size()-1;// 实际上位置0的元素是不使用的
while(N>1)//循环结束的条件是堆中元素等于1,即比该元素大的元素都按大小放到了它的后面,所以数组排序完毕
{
//首先将堆顶元素取出,交换到数组末尾
exch(a,1,N);
//删除体现为把数放置到数组末尾后,数组大小减小1->表示将最大值排除在外
--N;
//由于将原本堆末尾的数字交换到了堆顶,需要从上到下重新维护堆的性质
sink(a,1,N);
}
}
总结
堆排序在在初学的时候觉得很复杂,但是将堆排序的操作进行分解后,背后的原理很容易懂,这也充分体现了算法的有趣性,简单地预处理将大大提升排序算法的性能。
同时堆排序算法也是在初级的排序算法中,唯一能够最优地利用空间和时间的方法,在最坏情况下,它还能保证O(N logN)的时间复杂度,同时使用的仅仅是常数级的额外空间,但是在现代的很多应用中,很少使用到堆排序,这是因为它很少涉及相邻元素的比较和交换,无法有效利用缓存。
但是它背后包含的思想值得我们学习。堆的高效取最大值的操作在很多场合都有相应的应用,所以堆排序是值得我们细细品味学习的一个排序算法。



