算法分析与设计——动态规划法实验报告
|
算法导论 课程设计
题 目: 动态规划法
学院班级: 1613013 学 号: 16130130216 姓 名: 库 妍 主讲教师: 张立勇 日 期: 2019.4.11
|
(1)描述最优子结构:如果最优的加括号的方式将其分解为Ai..k与Ak+1..j的乘积,则分别对Ai..k与Ak+1..j加括号的方式也一定是最优的。
(2)递归定义最优解的值:定义m[i, j]为计算矩阵Ai..j所需标量乘法次数的最小值,对于i=j时,矩阵链乘只包含唯一的矩阵Ai,因此不需要做任何标量乘法运算,所以m[i, i]=0;当i<j时利用步骤(1)中的最优子结构来计算m[i, j]。所以,矩阵链乘的递归式为:
(3)按自底向上的方式计算最优解的值:在算法设计的时候,需要m数组记录Ai..j最小相乘次数,s数组记录构造最优解所需要的信息,其记录的k值指出了AiAi+1Aj的最优括号化方案的分割点应在AkAk+1之间。
(4)构造一个最优解。


4、项目测试(功能与性能)
矩阵链乘的时间复杂度为θ(n^3)
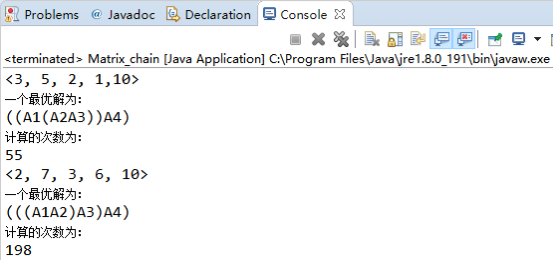
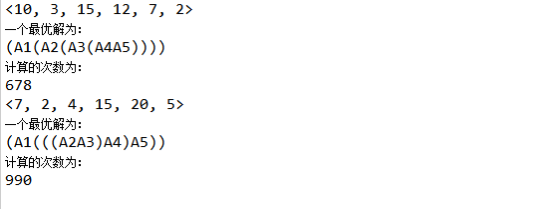
5、实验总结
动态规划在寻找问题的最优解时,问题解的代价通常是子问题的代价,不要忘记加上选择本身带来的开销。在阵链乘法问题中,首先要确定子链AiAi+1...Aj的最优加全部括号,然后选择矩阵Ak在该位置分裂乘积。选择本身所带来的开销为pi-1pkpj。
一、Longest Common Subsequence (LCS)
1、实验题目
用动态规划求下列字符串的最长公共子序列。
a)X: xzyzzyx Y: zxyyzxz
b)X:MAEEEVAKLEKHLMLLRQEYVKLQKKLAETEKRCALLAAQANKESSSESFISRLLAIVAD
Y:MAEEEVAKLEKHLMLLRQEYVKLQKKLAETEKRCTLLAAQANKENSNESFISRLLAIVAG
2、使用的算法
动态规划法
3、算法分析与设计
(1)描述一个最长公共子序列:令X=<x1,x2,..xm>和Y=<y1,y2,...,yn>为两个序列,Z=<z1,z2,...,zk>为X和Y的任意LCS。
①如果xm=yn,则zk=xm=yn且Zk-1是Xm-1和Yn-1的一个LCS。
②如果xm≠yn,则zk≠xm意味着Z是Xm-1和Y的一个LCS。
③如果xm≠yn,则zk≠yn意味着Z是X和Yn-1的一个LCS。
(2)递归定义最优解的值:定义c[i, j]为序列Xi和Yi的一个LCS长度。定义一个b[i, j]指向表项对应计算c[i, j]时所选择的子问题最优解,过程返回表b和表c,c[m, n]保持X和Y的LCS长度。
由LCS问题的最优子结构可得到递归式:
(3)按自底向上的方式计算最优解的值。
(4)由计算结果构造一个最优解。
4、项目测试(功能与性能)
LCS的时间复杂度为O(m+n),b表的空间复杂度为O(mn)。
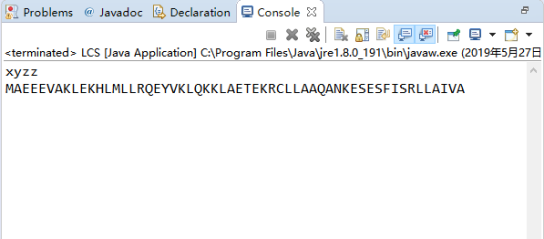
1、实验总结
算法可以有下面的改进,比如我们可以完全可以去掉表b。每个表项c[i, j]仅依赖于另外三个c表项:c[i-1, j-1],c[i-1, j],和c[i, j-1]。给定c[i, j]的值,我们可以在O(1)时间内确定这三个值中的哪一个被用来计算c[i, j]的,而不检查表b。利用一个类似于PRINT-LCS的过程,在O(m+n)时间内即可重构一个LCS。
一、Longest Common Substring
1、实验题目
用动态规划求下列字符串的最长公共子串。
a)X: xzyzzyx Y: zxyyzxz
b)X:MAEEEVAKLEKHLMLLRQEYVKLQKKLAETEKRCALLAAQANKESSSESFISRLLAIVAD
Y:MAEEEVAKLEKHLMLLRQEYVKLQKKLAETEKRCTLLAAQANKENSNESFISRLLAIVAG
2、使用的算法
动态规划法
3、算法分析与设计
(1)最优子结构:令X=<x1,x2,..xm>和Y=<y1,y2,...,yn>为两个序列,Z=<z1,z2,...,zk>为X和Y的任意最长公共子串。
①如果xm=yn,则zk=xm=yn且Zk-1是Xm-1和Yn-1的一个最长公共子串。
②如果xm≠yn,则zk≠xm意味着Z是Xm-1和Y的一个最长公共子串。
③如果xm≠yn,则zk≠yn意味着Z是X和Yn-1的一个最长公共子串。
(2)递归定义一个定义L[i, j]为以x[i]和y[j]为结尾的相同子串的最大长度。记录着X和Y的最长公共子串的最大长度。
最长公共子串的递归式:
(3)按自底向上的方式计算最优解的值。
(4)由计算结果构造一个最优解。
4、项目测试(功能与性能)
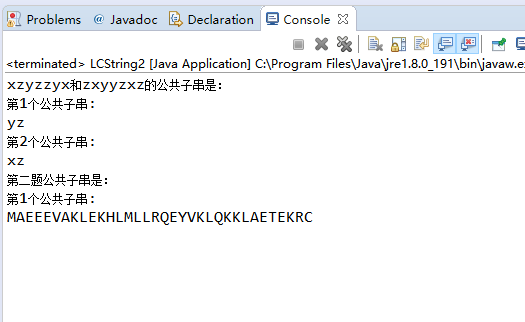
最长公共子串的时间复杂度为O(mn),空间复杂度为O(mn)。
5、实验总结
要同上述的最长公共子序列进行对比,区分他们的不同之处。也要理解用动态规划求解时的相同之处和不同之处。
一、Max Sum
1、实验题目
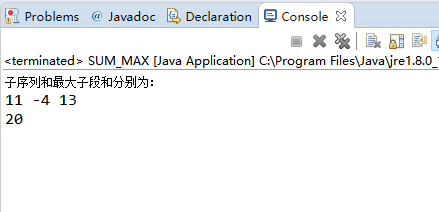
给定n个整数(可能为负数)组成的序列,a[1],a[2]...a[n],求该序列a[i]+a[i+1]...a[j]的子段和的最大值。
a)(-2,11,-4,13,-5,-2)
2、使用的算法
动态规划法
3、算法分析与设计
(1)描述最优子结构:定义当所给整数全为负数的时候,最大子段和为0,则最大子段和为max{0,a[i]+a[i+1]...+a[j]},1≤i≤j≤n
(2)递归定义最优解的值:引入一个辅助数组b,动态规划的分解分为两步: ①计算辅助数组的值。
②计算辅助数组的最大值。
辅助数组b[j]用来记录以j为尾的子段以及集合中的最大子段和。将每一个数是否列入当前子段作为一个决策,如果加上这个数后子段和仍然大于0,那么加上这个数;如果加上这个数后子段和小于0,那么子段清零,下一个数作为新的子段的开始在这个过程中记录遇到的最大子段和。
最大子段和的递归式:
(3)按自底向上的方式计算最优解的值。
(4)由计算结果构造一个最优解。
4、项目测试(功能与性能)
最大子段和使用动态规划进行计算的时间复杂度为O(n)。
5、实验总结
最大子段和问题求解方法有很多,还可以利用穷举法,穷举所有的[1,n]之间的区间,所以我们用两重循环,可以很轻易地做到遍历所有子区间。还可以分治法等方法求解。
五、Shortest path in multistage graphs
1、实验题目
利用动态规划法求出多段图中的最短路径。

2、使用的算法
动态规划法
3、算法分析与设计
(1)描述最优解的结构:设 是从顶点u到顶点v的最短路径, w是路径内部异于u和v的任一点,推断
和
也分别是从u到w和从w到v的最短路径。
(2)递归定义最优解的值:我们的目的是求0-15之间的最短路径,由图可知与节点15相连的是结点14和节点13,W(i,p)表示从源s 到v(i,p) 的最短路径长度。假设我们已经求出0-13的最短路径的值W13和0-14的最短路径的值W14,那么我们只需要比较W13 + w(13-15)和W14 + w(14-15)的大小就可以知道从哪个节点出发到节点15的路径最短。按照这个思想一直往前推,推到节点0时结束,自然就求出了节点0-节点15的最短路径,这个思路是递归的,如果用递归的方法,时间复杂度很高,当然你也可以用备忘录,记录已经计算过的值,我这里将递归转换成迭代。
最短路径的递归式为:
(3)按自底向上的方式计算最优解的值。
(4)由计算结果构造一个最优解。
4、项目测试(功能与性能)
时间复杂度为O(n^2)。

5、实验总结
求最短路径众所周知有Dijistra算法、Bellman-ford等,除了这些算法,用动态规划也可以求出最短路径,时间复杂度为O(n^2),跟没有优化的Dijistra算法一样(优化后的Dijistra算法时间复杂度为O((m+n)lgn))。


