算法分析与设计——分治法实验报告
|
算法导论 课程设计
题 目: 算法导论课程设计实验报告
学院班级: 1613013 学 号: 16130130216 姓 名: 库 妍 主讲教师: 张立勇 日 期: 2019.6.3 |
录
分治法
一、Implement exercise 2.3-7........................................4
二、Implement priority queue........................................6
三、Quicksort.......................................................8
四、找出第k大的元素...............................................10
动态规划法
一、Matrix-chain product...........................................13
二、Longest Common Subsequence (LCS)................................15
三、Longest Common Substring.......................................16
四、Max Sum........................................................18
五、Shortest path in multistage graphs.............................19
贪心法
一、Knapsack Problem...............................................22
二、scheduling problem.............................................23
三、Single-source shortest paths...................................24
四、All-pairs shortest paths.......................................26
回溯法
一、0/1 Knapsack Problem...........................................29
二、8-Queen problem................................................30
|
算法导论 课程设计
题 目: 分 治 法
学院班级: 1613013 学 号: 16130130216 姓 名: 库 妍 主讲教师: 张立勇 日 期: 2019.3.21 |
一、Implement exercise 2.3-7
1、实验题目
描述一个运行时间为O(nlgn)的算法,给定n个整数的集合S和另一个整数x,该算法能确定S中是否存在两个其和刚好为x的元素。
2、使用的算法
(1)运用归并排序算法,先对集合中的整数进行排序。
(2)归并排序后,运用二分查找两个数和为x的元素。
3、算法分析与设计
(1)首先将S进行排序,然后再通过查找算法进行查找。插入排序算法复杂度最差O(n^2),归并排序最差为O(nlgn),堆排序为最差为O(nlgn),快速排序最差为O(n^2),这里直接使用归并排序。归并排序运用的是分治思想,时间复杂度为 O(nlgn),能够满足题目要求的运行时间。
①分解(devide):归并排序将n个元素分成各含n/2g个元素的子序列,对已经分解的两个部分再进行分解直到将数组分解成单个元素为止。
②解决(conquer):用合并排序法递归求解排序子序列。
③合并(combine):合并部分是将已经排序的两个子序列进行合并得到结果。
(2)二分查找又称折半查找,优点是比较次数少,查找速度快,平均性能好,占用系统内存较少。折半查找法也称为二分查找法,它充分利用了元素间的次序关系,采用分治策略,可在最坏的情况下用O(lg n)完成搜索任务。它的基本思想是,将n个元素分成个数大致相同的两半,取a[n/2]与欲查找的x作比较,如果x=a[n/2]则找到x,算法终止。如 果x<a[n/2],则我们只要在数组a的左半部继续搜索x(这里假设数组元素呈升序排列)。如果x>a[n/2],则我们只要在数组a的右 半部继续搜索x。


1、项目测试(功能与性能)
时间复杂度为O(nlgn)
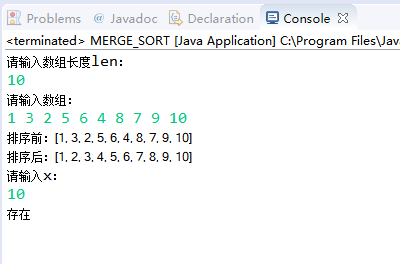

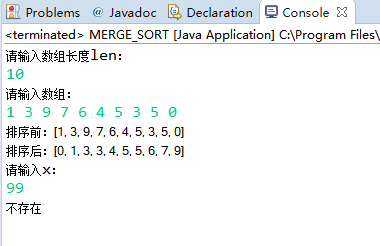
1、实验总结
遇到的问题及解决:
MERGE过程中,子数组A[p..q]和A[q+1..r],待合并个数n1 = q - p + 1,n2 = r - q,计算时容易出错。
另外,进行二分查找时right = A.length - 1,数组最后一个元素的下标是数组A的长度减1。
二、Implement priority queue
1、实验题目
实现优先级队列,即需要支持以下操作:INSERT(S,x):把元素x插入到集合S中;MAXMUM(S):返回S中具有最大key的元素;EXTRACT-MAX(S):去掉并返回S中的具有最大key的元素; INCREASE-KEY(S,x,k):将元素x的关键字值增到k。
2、使用的算法
运用堆排序,来实现优先队列。
3、算法分析与设计
(1)堆排序是利用堆这种数据结构而设计的一种排序算法,堆排序是一种选择排序,它的最坏,最好,平均时间复杂度均为O(nlogn),它也是不稳定排序。堆排序算法分为3个过程,MAX-HEAPIEY:调整堆以满足小顶堆性质,其时间复杂度为O(lgn);BUILD-MAXHEAP:从无序的输入数据数组中构造小顶堆,其时间复杂度为线性时间;HEAP-SORT:对数组进行原址排序,其时间复杂度为O(nlgn)。
(2)在堆的基础上实现优先队列INSERT、MAXMUM、EXTRACT-MAX、INCREASE-KEY,时间复杂度为O(lgn)。


4、项目测试(功能与性能)
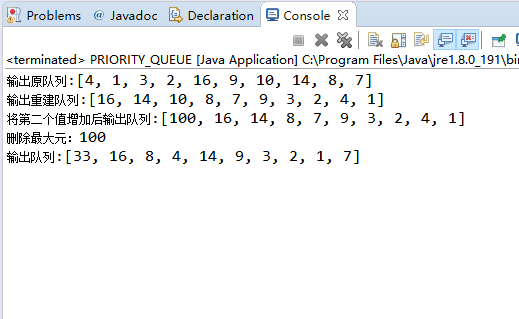
1、实验总结
编写HEAP-EXTRACT-MAX函数的时候,当去掉第一个元素后,程序要调用MAX-HEAPIFY进行调整堆,否则最后序列是无序状态。另外,开始没有理解BUILD-MAX-HEAP的过程,当对某结点调用BUILD-MAX-HEAP时,该结点的两棵子树都已是最大堆。
三、Quicksort
1、实验题目
实现quick_sort算法,并且回答以下两个问题:
(1)待排数组中的元素值都相同的情况下,运用quick_sort需要进行多少次比较?
(2)对于n个元素的数组,运用quick_sort举出需要进行比较次数的上限和下限是多少?
2、使用的算法
使用了快速排序算法。
3、算法分析与设计
快速排序采用分治策略,时间复杂度为O(nlgn),但是最坏情况下为O(n2),并且快速排序算法属于原地排序,并不需要开辟空间。快速排序复杂的步骤为其分解的步骤。
①分解(divide):数组A[p..r]被划分为两个子数组A[p..q-1]和A[q+1..r], 使得A[p..q-1]中的每个元素都小于等于A[q],而且,小于等于A[q+1..r] 中的每个元素。下标q也在这个划分过程中进行计算。
②解决(conquer):通过递归调用快速排序,对子数组A[p..q-1]和A[q+1..r] 进行排序。
③合并(combine):因为两个子数组是就地排序的,将它们的合并不需要操 作,整个数组A[p..r]已排序。

4、项目测试(功能与性能)
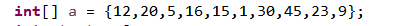
5、实验总结
问题回答:
(1)当选择第一个或最后一个参考点时,当n个元素相同时为最坏情况,比较的数目是n *(n-1)/ 2。
(2)快速排序比较的最小数目是nlgn,最大的比较数是n^2。
四、找出第k大的元素
1、实验题目
运用分治的策略将两个已经排好序的序列中,找出第k大的元素,且要求时间复杂度为O(lgm + lgn),其中m和n分别为两个序列的长度。
2、使用的算法
使用分治策略
3、算法分析与设计
解法一:
(1)分解:因为已经是两个独立的的序列,所以不用进行分解。
(2)解决:因为两个序列为已经排好的序列,因此不用分开进行排序。
(3)利用归并排序中的merge函数,将这两个序列分别看成是L[]和R[]两个数组,通过开辟一个新的数组,将两个数组合并成一个新的排好序的序列,在根据要求的k值,对新的数组进行取值。
解法二:题目只要求第k大的数,没必要花力气将数组全部再排序,可以定义两个游标分别指向两个有序数组,按序移动,并用count计数,当count等于k时,返回两个游标指向的数中最小的那一个。
4、项目测试(功能与性能)
时间复杂度为O(lgm + lgn)。
5、实验总结
理解分治策略的三个步骤:分解、解决和合并在具体问题上的应用,根据时间复杂度与所学的算法进行结合。为了解决一个问题,算法要一次或多次地调用其自身来解决相关的子问题,这些算法常采用分治策略。分治法将原问题划分成n个规模较小而结构与原问题相似的子问题,递归地解决这些子问题,然后合并其结果,得到子问题的解。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号