遗传算法:N皇后
N皇后问题描述
N皇后问题是一个经典的问题,在一个N*N的棋盘上放置N个皇后,每行一个并使其不能互相攻击(同一行、同一列、同一斜线上的皇后都会自动攻击)。

遗传算法
遗传算法是局部束搜索的变形: 与自然选择过程相似,通过把两个父代结合产生后继(有性繁殖),而不是修改单一状态(无性繁殖)。
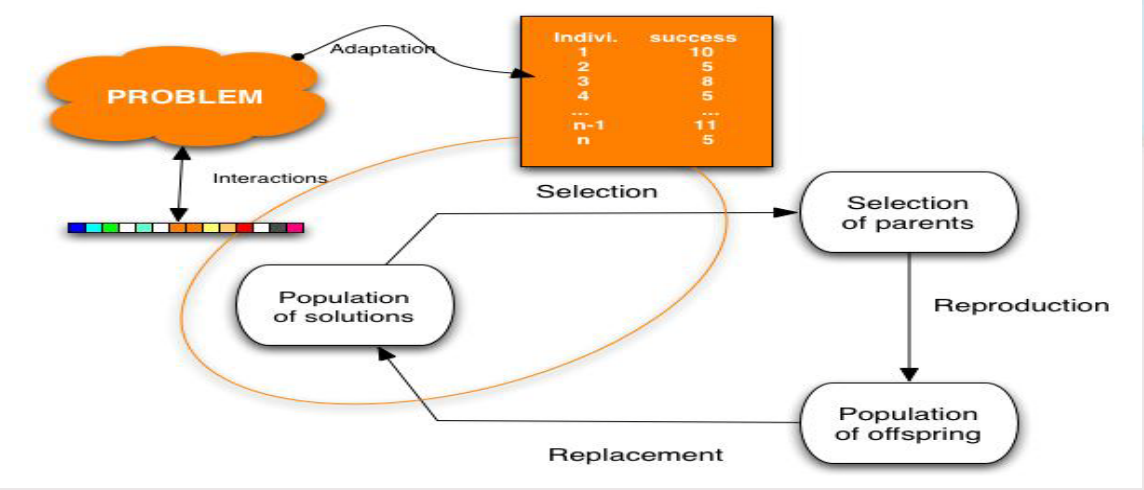
1、通过结合两个状态来产生后继状态
2、从k个随机产生的状态开始(种群)
3、状态表示成字符串(染色体)
4、评估函数(适应值函数)
5、通过选择(轮盘赌选择法)、交叉(杂交)和变异操作来产生新一代种群
6、半性繁殖的局部束搜索
7、适应值函数:相互攻击不到的皇后对数
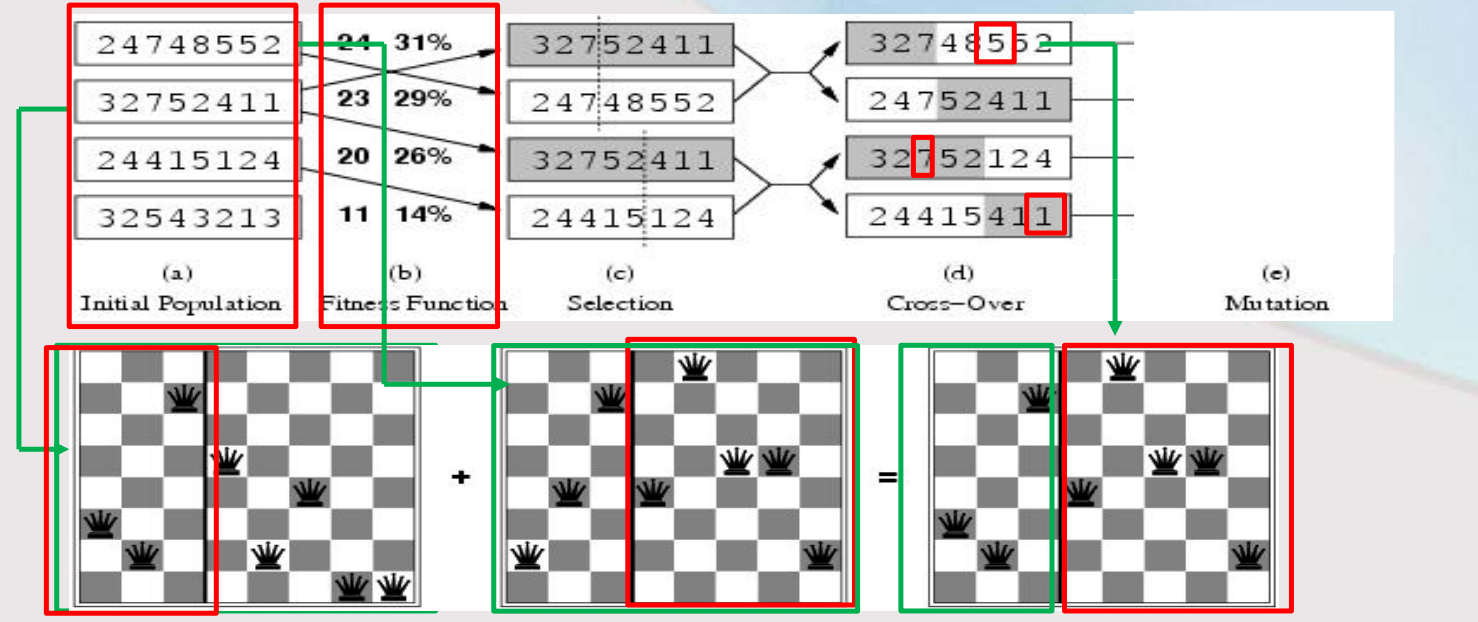
轮盘赌选择法
轮盘赌选择法是依据个体的适应度值计算每个个体在子代中出现的概率,并按照此概率随机选择个体构成子代种群。轮盘赌选择策略的出发点是适应度值越好的个体被选择的概率越大。因此,在求解最大化问题的时候,我们可以直接采用适应度值来进行选择。但是在求解最小化问题的时候,我们必须首先将问题的适应度函数进行转换,以将问题转化为最大化问题。下面给出最大化问题求解中遗传算法轮盘赌选择策略的一般步骤:
(1) 将种群中个体的适应度值叠加,得到总适应度值==1 ,其中 为种群中个体个数。
(2) 每个个体的适应度值除以总适应度值得到个体被选择的概率
(3) 计算个体的累积概率以构造一个轮盘。
(4) 轮盘选择:产生一个[0,1]区间内的随机数,若该随机数小于或等于个体的累积概率且大于个体1的累积概率,选择个体进入子代种群。
重复步骤(4)次,得到的个体构成新一代种群。
图 3.4 染色体的轮盘赌式选择
伪代码:
//主循环
void Genetic::GeneticAlgorithm()
while m_NotSuccess为真
Select
Crossover
Mutate
End while
打印最优解
End
//计算一个state(棋盘)的适应值
//适应值采用“互相攻击皇后对的个数的倒数”,这比书上直接计算不互相攻击的皇后对数作为适应值的方法相比,更能拉开不同状态之间的差距。
//@para state:一个状态的引用
double Genetic::CalcuAdaptive(vector &state)
counter←0
For i: 0 to QueenNum-1 do
For i: 0 to QueenNum-1 do
If 对角线方向互相攻击,或者垂直方向互相攻击
counter++
End if
End for
End for
If counter等于0
m_NotSucess←false,程序的循环终止条件
m_BestOne←state,保存当前的状态
End if
Return 1.0/counter
End
//自然选择,大体思路是轮盘赌选择
void Genetic::Select()
创建一个新的空种群newPopulation
For i: 1 to populationSize-1 do
m_accumuAdaptive[i]←m_accumuAdaptive[i - 1] + m_adaptive[i]
End for
totalAdaptive←m_accumuAdaptive的最后一个元素
For i: 0 to populationSize-1 do
先把totalAdaptive(这是一个实数)放大成一个整数
产生一个随机数 ,对totalAdaptive求模,得到 ran
按相同比例缩小成一个实数
用二分查找的方法,在m_ accumuAdaptive内进行查找 ran,找出位置 j
把m_population的第 j 个状态push_back到newPopulation中
End for
m_population←newPopulation
End
杂交有多种思路:
- 选择两个state状态,随机产生一个杂交点,然后对这个杂交点的右(左)边的“基因”进行交换
- 选择两个state状态,随机产生一个杂交点,然后再对这个杂交点两边的“基因”都进行交换。
- 选择两个state状态,随机产生两个杂交点,然后再对这两个杂交点之间的“基因”进行交换。
变异:
通过伪随机数,使每一个基因有0.0几的概率进行突变。突变就是用伪随机数赋值。
代码实现
Genetic.h
#pragma once #include <iostream> #include <cstdlib> #include <iomanip> #include <algorithm> #include <vector> #include <ctime> #include <cmath> #include <fstream> using namespace std; class Genetic { private: int m_Num; // 皇后数量 bool m_IsSuccess; // 是否成功找到最优解 vector<int>m_optimalSolution; // 最优解. vector<vector<int> >m_population; // 种群 vector<double>m_adaptive; // 种群的适应值(1/冲突数)。 vector<double>m_AdaptValue; // 累积的适应值(定位哪一个被选中的) public: Genetic(int numOfQueens, int initialGroupNum); double CalcuAdaptive(vector<int> &state); // 计算适应值(互不相攻击的皇后对数) void SetPopulation(); void Choose(); // 选择 void GeneticCrossover(); // 杂交 void GeneticMutate(); // 变异 void GeneticCalculation(); void Print(); // 打印最优解 };
Genetic.cpp
Genetic::Genetic(int numOfQueens, int initialGroupNum) { m_adaptive.resize(initialGroupNum, 0); m_AdaptValue.resize(initialGroupNum, 0); m_Num = numOfQueens; m_IsSuccess = true; SetPopulation(); } void Genetic::SetPopulation() { m_population.clear(); vector<int> tmpState(m_Num, 0); for (int i = 0; i < m_adaptive.size(); ++i) { for (int j = 0; j < m_Num; ++j) // 初始化 tmpState[j] = rand() % m_Num; m_population.push_back(tmpState); m_adaptive[i] = CalcuAdaptive(tmpState); } } double Genetic::CalcuAdaptive(vector<int> &state) { int conflict = 0; for (int i = 0; i < m_Num; ++i) { for (int j = i + 1; j < m_Num; ++j) { //如果对角线方向互相攻击,或者垂直方向互相攻击 if (state[i] == state[j] || abs(state[i] - state[j]) == j - i) conflict++; } } if (conflict == 0) { // 找到最优解 m_IsSuccess = false; m_optimalSolution = state; //保存当前的状态 } return 1.0 / conflict; } //自然选择(大体思路是轮盘赌选择) void Genetic::Choose() { vector<vector<int>> NewPopulation; //创建一个新的空种群NewPopulation m_AdaptValue[0] = m_adaptive[0]; for (int i = 1; i < m_AdaptValue.size(); i++) m_AdaptValue[i] = m_AdaptValue[i - 1] + m_adaptive[i]; double totalAdaptive = m_AdaptValue[m_AdaptValue.size() - 1]; //避免陷入局部最优解(不直接选择适应值最高的两个进行杂交) for (int i = 0; i < m_population.size(); i++) { //比例缩放的轮盘赌 int magnifyTotalAdaptive = totalAdaptive * 100000; //实数->整数(放大) int random = (rand()*rand()) % magnifyTotalAdaptive;//转动轮盘 double select = (double)random / 100000; //按相同比例缩小 //int select = rand()*rand() % ((int)totalAdaptive); vector<double>::iterator indexi; //二分查找: 在m_AdaptValue中查找适应值与select最接近的个体的下标 indexi = lower_bound(m_AdaptValue.begin(), m_AdaptValue.end(), select); int indexj = indexi - m_AdaptValue.begin(); //加入新的种群中 NewPopulation.push_back(m_population[indexj]); } // 更新种群 m_population.clear(); m_population = NewPopulation; } void Genetic::GeneticCrossover() { //杂交==>交换基因片段(皇后位置进行交换) int first = 0; int row1; for (int i = 0; i < m_population.size(); i++) { if (rand() % 2) { ++first; if (first % 2 == 0) { int crossPoint = rand() % (m_Num - 1); for (int j = crossPoint; j < m_Num; j++)swap(m_population[row1][j], m_population[i][j]); //值交换 } else row1 = i; } } } void Genetic::Print() { for (int i = 0; i < m_optimalSolution.size(); ++i) { for (int j = 0; j < m_optimalSolution.size(); ++j) { if (j == m_optimalSolution[i]) cout << "Q "; else cout << ". "; }cout << '\n'; }cout << '\n'; } //随机突变=> 随机改变某个个体的某个基因(随机改变某个地图中的某个皇后的位置) void Genetic::GeneticMutate() { int mutateSpot = 0; for (int i = 0; i < m_population.size(); ++i) { if (rand() % 2 == 0) { mutateSpot = rand() % m_Num; m_population[i][mutateSpot] = rand() % m_Num; } m_adaptive[i] = CalcuAdaptive(m_population[i]); // 更新适应值 } } void Genetic::GeneticCalculation() { clock_t start, finish; start = clock(); while (m_IsSuccess) { // 自然选择 Choose(); // 杂交 GeneticCrossover(); // 变异 GeneticMutate(); } //打印最优解 //if (m_Num<25) Print(); Print(); finish = clock(); cout << "遗传算法求解时间: " << finish - start << "ms" << endl; }
main.cpp
#include"Genetic.h" int main() { int numOfQueen; cout << "请输入皇后数目: "; cin >> numOfQueen; cout << "【遗传算法求解】" << endl; Genetic Q(numOfQueen, 120); Q.GeneticCalculation(); system("pause"); }
运行结果:
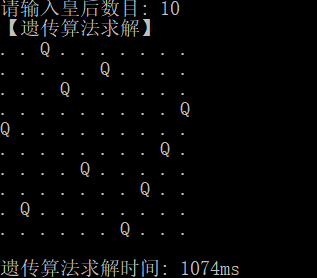
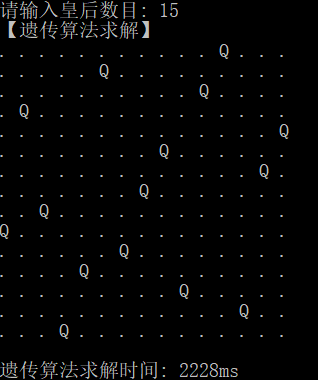


 浙公网安备 33010602011771号
浙公网安备 33010602011771号