朴素贝叶斯

基本思想

　　朴素贝叶斯是基于贝叶斯定理与特征条件独立假设的分类方法 。

　　

 基本方法

　　定义输入空间 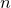（维向量集合），输出空间 。

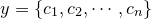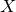　　输入：特征向量  ，输出：类别标记；是和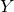的联合概率分布。

　　训练集

　　　　　　　　

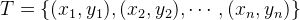
　　由独立同分布产生。

　　由于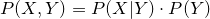，故我们必须先学得先验概率分布和条件概率分布。

　　先验概率分布：

　　　　　　　　

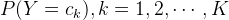
　　条件概率分布：

　　　　　　　　

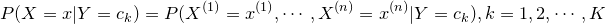
　　注：条件概率分布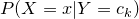有指数级的参数数量，不能直接估计（假设可取值有个，Y的可能取值有K个，则参数个数为）

 　　

　　朴素贝叶斯法对条件概率分布作出了条件独立性的假设 。具体地，条件独立性假设是 ：

　　　　　　　　

　　

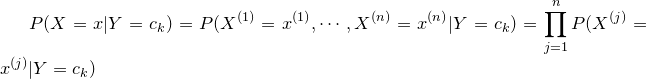
 　  朴素贝叶斯法分类时，对给定的输入x，通过学习到的模型计算后验概率分布 ，将后验概率最大的类作为x的类输出 。后验概率计算根据　　　   贝叶斯定理进行 ：

　　　　　　　

　　　　　　　　　　

 　　　　　　  

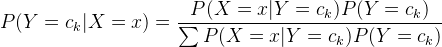
　　这便是朴素贝叶斯法分类的基本公式。于是，朴素贝叶斯分类器可以表示为

　　　　　　　

　　注意到，上式中分母对所有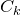都是相同的，所以：

　  　

 

 

 

 

 

　

 

 

 

 

 

 

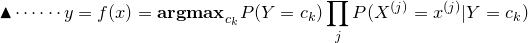
x⊆Rn

x⊆Rn

x⊆Rn