高中文化课技巧总结

Last Updated: 6/18/2020

数学

TODO

超几何分布
一些咕了的内容

基础姿势

不等式

平均数

下面式子从左到右分别叫调和平均数、几何平均数、算术平均数和平方平均数，等号成立的条件均为 \(x_1=x_2=\ldots=x_n\)。

\[\large{\frac{1}{~~~\frac{\sum\limits_{i=1}^{n}\frac{1}{x_i}}{n}~~~}\leq\sqrt[n]{\prod\limits_{i=1}^{n}x_i}\leq\frac{\sum\limits_{i=1}^{n}x_i}{n}\leq \frac{\sum\limits_{i=1}^{n}x_i^2}{n}} \]

另外还有 \(x_1^2+x_2^2\geq 2x_1x_2\)。

柯西不等式：选修 4-5 P39

等号成立：\(\vec{a}=\lambda \vec{b}\)。

\[\sum\limits_{i=1}^{n}a_i^2\times\sum\limits_{i=1}^{n}b_i^2\geq(\sum\limits_{i=1}^{n}(a_ib_i))^2 \]

绝对值不等式

本节部分内容待考证。
\(|a|-|b|\leq |a-b|\leq |a\pm b|\leq |a|+|b|\)，等号成立条件为 \(ab\geq 0\)。

指数不等式、对数不等式

\(x+1\leq e^x\)，\(x=0\) 时等号成立。
\(x-1\geq\ln x\)，\(x=1\) 时等号成立。

排列组合及二项式定理

• \(A_{n}^{m}=\frac{n!}{(n-m)!}\)
• \(C_{n}^{m}=\frac{A_{n}^{m}}{m!},~\sum\limits_{i=0}^{n}C_n^i=2^n\)
• \((a+b)^n=\sum\limits_{i=0}^{n}C_n^ia^nb^{n-i}\)

Misc

• \(a^3\pm b^3=(a\pm b)(a^2\mp ab+b^2)\)
• \(\log_ab=\frac{1}{\log_ba}\)
• \(\frac{a+b}{ab}=\frac{1}{a}+\frac{1}{b}\)
• 奇变偶不变，符号看象限

初中复习

• 直径所对圆周角为 \(\frac{\pi}{2}\)
• 切点与圆心的连线与切线垂直。

选择题

• \(\frac{y-z_2}{x-z_1}\) 考虑过 \((z_1,z_2)\) 的直线斜率。
• 遇到范围题代入范围边界排除，以及选取一些可以帮助排除的特值。
• 遇到 \(P_{1,2}(\pm x,0)\) 考虑轨迹为双曲线或椭圆，在 \(x=0\) 时验证是否符合题意可排除双曲线。
• \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=\lambda~(\lambda\neq 0)\) 双曲线族的渐近线相同，为 \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=0\)。

以下“蒙题”为在绝对没有思路的情况下的做法，请勿一开始就使用。

求 \(f(f(x))=1\) 的根的个数

\[f(x)=\begin{cases}\begin{align} \nonumber kx+1\qquad &x\leq 0 \\ \nonumber \ln x\qquad &x>0 \\ \end{align} \end{cases} \]

此处笔记遗失，见谅。
解 \(f(x)=1\) 得 \(x=0\) 或 \(x=e\)

印象中是画图？
当 \(f(x)=0\) 时有几个根，\(f(x)=e\) 时有几个根，加和得三个。

对称性、周期性

对称性

\[\begin{align} f(x+2)&=f(-x)\qquad &关于~x=\frac{x+2-x}{2}=1~对称\qquad\\ f(x+2)+f(-x)&=2b&关于~(\frac{x+2-x}{2},b)~中心对称\\ f(x+2)&=-f(x)&关于~(\frac{x+2-x}{2},0)~中心对称\\ \end{align} \]

上面三个式子从上到下编号 \((1),~(2),~(3)\)。
可以发现式 \((3)\) 是式 \((2)\) 在 \(b=0\) 时的特例。

周期性

\[\begin{align} f(x-1)&=f(x+1)\qquad &T=2 \\ f(x+2)&=-f(x)\qquad &T=4\\ f(x+1)&=-f(x-1)\qquad &T=4\\ \end{align} \]

上面三个式子从上到下编号 \((4),~(5),~(6)\)。
可以发现 \((6)\) 式两侧的 \(f(t)\) 的 \(t\) 同减 \(2\) 得 \(f(x+1)=-f(x-1)=f(x-3)\)，即得 \(T=4\).

已知定义在 \(\mathbb{R}\) 上的奇函数符合 \(f(x+2)=f(-x)\)。

则可知 \(f(x)\) 关于 \(x=1\) 对称。由奇函数得 \(f(-x)=-f(x)\)，即 \(-f(x)=f(x+2)\)，可得周期 \(T=4\)。

不等式

蒙题

• 尝试动直线过圆心

拉格朗日乘数法

1

也叫拉格朗日乘子法（🍊），可以见 KSkun 的这篇博文，其中关于偏导数的知识请参见此处。
此处展示另一题例题。

(2019·深圳模拟）已知 \(a>1,~b>0,~a+b=2\)，求 \(\frac{1}{a-1}+\frac{1}{2b}\) 的最小值。（选择题）

\(a+b=2\Rightarrow a+b-2=0\).
首先有 \(L=\frac{1}{a-1}+\frac{1}{2b}+\lambda(a+b-2)\)

\[\begin{cases} \frac{\partial L}{\partial a}=-(a-1)^{-2}+\lambda=0\\ \frac{\partial L}{\partial b}=-2\cdot(2b)^{-2}+\lambda=-(2b^2)^{-1}+\lambda=0\\ \frac{\partial L}{\partial\lambda}=a+b-2=0 \end{cases} \]

得 \((a-1)^2=2b^2\)，即 \((a-1)^2=2\cdot (2-a)^2\)，解得 \(a=3\pm \sqrt{2}\)。

\(a=3+\sqrt{2}\) 时 \(b<0\)，舍去，即 \(a=3-\sqrt{2}\)，得 \(b=\sqrt{2}-1\)。

代入得 \(\frac{1}{a-1}+\frac{1}{2b}=\frac{3}{2}+\sqrt{2}\)

2

有时题目中并没有一个等式来表明限制，此时可以忽略拉格朗日乘数。注意使用这个做法时是可能出现鞍点的，因此存在一定风险。

已知 \(a>b>0\)，求 \(a^2+\frac{16}{b(a-b)}\quad (*)\) 的最值。

令 \(L=a^2+\frac{16}{b(a-b)}\).

\[\begin{align} \nonumber \begin{cases} &\frac{\partial L}{\partial a}=2a-16b\cdot\frac{1}{(ab-b^2)^2}\qquad &(1)\\ &\frac{\partial L}{\partial b}=-16(a-2b)\cdot\frac{1}{(ab-b^2)^2}\qquad &(2) \end{cases} \end{align} \]

由 \((2)\) 得 \(a=2b\)，代入 \((1)\) 解得 \(b=\sqrt{2}\)，即 \(a=2\sqrt{2}\)，代入 \((*)\) 得 \(16\)。

数列

• 将形如 \(r^{kn-t}\) 的形式转化成 \(\large{\frac{(r^k)^n}{r^t}}\) 的形式再求 \(S_n\)，避免运算错误。
  • 例如 \(2^{2n-1}\) 转化成 \(\frac{4^n}{2}\)。
• 如果对一个式子没有头绪，尝试：
  • 有理化
• 递推式没法转成通项式时尝试变形，使两边具有相同的形式，然后对这个等差/等比数列求通项公式，适当变形即得原数列通项公式。
  • \(a_{n+1}=3a_n+2\Rightarrow a_{n+1}-a_{n}=2(a_n+1)\)
  • \(a_{n+2}=3a_{n+1}-2a_n\Rightarrow a_{n+2}-a_{n+1}=2(a_{n+1}-a_{n})\)
• \(a_{n+1}=pa_n+q\Rightarrow a_{n+1}=pa_n+q+\frac{q}{p-1}=pa_n+\frac{pq-q+q}{p-1}=pa_n+\frac{pq}{p-1}=p(a_n+\frac{q}{p-1})\)
• \(t^{n+1}-t^n=t^n(t-1)\)
• 单调性：相邻项做差做商

递推转通项

遇到形如 \(a_n=a_{n-1}+\textit{expr}\) 的将 \(a_i\) 移到同一侧。

\(a_{n+1}=a_n+n+1\)

\[d_1=a_2-a_1=2\\ d_2=a_3-a_2=3\\ \cdots\\ d_n=a_n-a_{n-1}=n+1\\ \sum\limits_{i=1}^{n} d_i=a_n-a_1=\sum\limits_{i=2}^{n+1}i\\ \therefore a_n=\sum\limits_{i=2}^{n+1}i+a_1 \]

求 \(S_n\) 转为求 \(a_n\)

等差数列

令 \(k=\frac{i+1}{2}\)，\(i\) 为奇数，有 \(S_i=\frac{i(a_1+a_i)}{2}=\frac{i\cdot(2a_k)}{2}=i\cdot a_k\)。有时候用这个方法反推回 \(S_i\)。

等比数列

• \(\large{\frac{S_{2m}}{S_m}=\frac{\frac{a_1(1-q^{2n})}{1-q}}{\frac{a_1(1-q^{n})}{1-q}}=\frac{1-q^{2n}}{1-q^n}=\frac{(1-q^{2n})(1+q^n)}{1-q^{2n}}=1+q^n}\)

已知 \({b_n}\)，证明 \({a_n}\) 是等比数列

将 \(a_n\) 变形成 \(b_n\) 的形式，且该形式下相邻两项为倍数关系。

（2018·全国卷II）已知 \(na_{n+1}=2(n+1)a_n\)，证明 \(b_n=\frac{a_n}{n}\) 为等比数列。

\(\frac{a_{n+1}}{n+1}=2\frac{a_n}{n}\)，即 \(b_{n+1}=2b_n\)。

数列求和

错位相减法

遇到形如 \(a_n=n\cdot q^{n-1}\) 这类 \(n\) 与 \(q^n\) 相乘的通项，求 \(S_n\) 时尝试与 \(q\cdot S_n\) 错位相减：

\[\begin{align} S_n&=q^0\cdot 1+q^1\cdot 2+\cdots+q^{n-2}\cdot(n-1)+q^{n-1}\cdot n \nonumber\\ q\cdot S_n&=q^1\cdot 1+q^2\cdot 2+\cdots+q^{n-1}\cdot (n-1)+q^n\cdot n \nonumber\\ (1-q)\cdot S_n&=q^0\cdot 1+q^1\cdot (2-1)+\cdots+q^{n-1}\cdot (n-(n-1))-q^n\cdot n \nonumber\\ &=q^0+q^1+\cdots+q^{n-1}-q^n\cdot n \nonumber\\ &=\frac{1-q^{n}}{1-q}-q^n\cdot n \nonumber \end{align} \]

三角函数

前置知识

• 正弦定理、余弦定理
• 升降幂：\(cos^2\alpha=\frac{1+\cos 2\alpha}{2},~sin^2\alpha=\frac{1-cos2\alpha}{2}\)
• \(cos^2\alpha = \frac{1}{1+\tan\alpha}\)
• \(CD\) 为中线，有 \(\vec{CD}=\frac{\vec{CA}+\vec{CB}}{2}\)。
• \((\vec{a}\pm\vec{b})^2=|\vec{a}|^2+|\vec{b}|^2\pm\vec{a}\cdot\vec{b}=|\vec{a}|^2+|\vec{b}|^2\pm|\vec{a}||\vec{b}|\cos C\)

常用技巧

一边一角考虑余弦定理。

1

已知 \(\sin\theta+\cos\theta=\frac{1}{5}~(1)\)，求 \(\sin\theta,~\cos\theta,~\tan\theta\).

\[\tag{2} (\sin\theta+\cos\theta)^2=(\frac{1}{5})^2=1+2\sin\theta\cos\theta\Rightarrow\sin\theta\cos\theta=-\frac{12}{25} \]

\[\tag{3} \sin\theta-\cos\theta=\sqrt{(\sin\theta+\cos\theta)^2-4\sin\theta\cos\theta~}=\frac{7}{5} \]

\((1)+(3)\) 得 \(2\sin\theta=\frac{8}{5}\)，即 \(\sin\theta=\frac{4}{5}~(4)\)；
\((1)-(4)\) 得 \(\cos\theta=-\frac{3}{5}~(5)\)；
由 \((4),~(5)\) 得 \(\tan\theta=-\frac{4}{3}\)。

求面积最大最小值

1：给的边是 \(a\)，给的角是 \(A\)。

先转化成 \(a^2=b^2+c^2-2bc\cos A\)，把值代入，这样就得到了一个 \(k_1=b^2+c^2-2bc\cdot k_2\) 的形式，由不等式得 \(k_1\geq (2-k_2) bc\)，即 \(bc\leq \frac{k_1}{2-k_2}\)，代入 \(S=\frac{1}{2}bc\sin A\) 即可。

求面积/周长值

一般通过余弦定理获得关于 \(ab\) 的一个表达式，然后通过另一个条件等（如正弦定理）获得 \(ab\) 的另一个表达式，联立解出 \(ab\)，代回解出 \(a+b\)，\(a^2+b^2=(a+b)^2-2ab\) 等，代入周长/面积公式中即可。

1：已知中线 \(CD=l_1\)，角 \(C\)，边 \(c\)

\(\vec{CD}=\frac{\vec{CA}+\vec{CB}}{2}\Rightarrow 4|\vec{CD}|^2=|\vec{CA}|^2+|\vec{CB}|^2+2|\vec{CA}||\vec{CB}|\cos C\Rightarrow 4l_1^2=a^2+b^2+2ab\cos C~(1)\)

\(\cos C=\frac{a^2+b^2-c^2}{2ab}\Rightarrow c^2=a^2+b^2-2ab\cos C~(2)\)

\((1)+(2)\) 得 \(2(a^2+b^2)=c^2+4l_1^2\)，即 \(a^2+b^2=\frac{c^2+4l_1^2}{2}\)。

代回 \((1)\) 或 \((2)\) （这里以 \((2)\) 为例子）得 \(c^2=\frac{c^2+4l_1^2}{2}-2ab\cos C\)，即 \(ab=\frac{c^2-\frac{c^2+4l_1^2}{2}}{-2\cos C}\)。

代入 \(S=\frac{1}{2}ab\sin C\) （注意这里是 \(\textbf{sin}\)）得 \(\large{S=\frac{~c^2-\frac{c^2+4l_1^2}{2}~}{-4\cos C}}\sin C\)。

这里全程用了代数运算所以得的结果有点毒瘤，\(ab\) 和 \(a^2+b^2\) 用数字替换了以后就正常多了。

2

（2017·全国卷I）已知 \(\sin B\sin C=\frac{2}{3},~\cos B\cos C=\frac{1}{6},~a=3\)，求 \(C_{\triangle ABC}\)。

\(\cos B\cos C-\sin B\sin C=\cos (B+C)=-\cos A=\frac{1}{2}\Rightarrow A=\frac{\pi}{3}, \sin A=\frac{\sqrt{3}}{2}\)
然后正弦定理可得 \(bc=\frac{a^2}{\sin^2 A}\cdot\sin B\sin C=8\)
余弦定理可得 \(a^2=b^2+c^2-bc=9\)
联立可得 \(b+c=\sqrt{33}\)，即 \(C=a+b+c=3+\sqrt{33}\)

圆锥曲线

• 尝试建立题面描述的情景与定义之间的关系
• 第一问一般不会用到太复杂的方法，考虑定义。
  - 椭圆：\(|\text{PF}_1|+|\text{PF}_2|=2a\)
  - 双曲线：\(|\text{PF}_1|-|\text{PF}_2|=2a\)
  - 抛物线：\(p\) 为焦准距
• 尝试纯几何方法
• 交点：联立，得到一个关于 \(x\) 和未知数 \(k\) 啥的的方程，韦达表示出 \(x_1+x_2=-\frac{b}{a},~x_1x_2=\frac{c}{a}\)。然后用 \(A(x_1,y_1),~B(x_2,y_2)\) 表示出满足题目要求的式子，用韦达的结果化简，得到式子。
• 同时出现 \(P,F_1,F_2\) 考虑 \(|F_1|\pm|F_2|\)，即 \(2a\)，出现焦点三角形，有角度，考虑余弦定理。
• \(\vec{\text{AB}}=(x_2-x_1,~y_2-y_1)\Rightarrow \vec{t}=\lambda\vec{\text{AB}}=(1,\frac{y_2-y_1}{x_2-x_1})\)，\(\vec{t}\) 称为 \(\vec{\text{AB}}\) 的方向向量。

• \[不建议使用：\\\\\begin{cases}y^2=4x \\y=kx+b \\\end{cases}\\建议使用：\\\begin{cases}y^2=4x \\x=ky+b\end{cases} \]

• 有时替换一下式子里的常数成 \(x_1x_2,~x_1+x_2\) 等有利于做题。
• 求四边形面积：
  - 对角线垂直：\(S=\frac{1}{2}|\text{MN}||\text{PQ}|\)
  - 三角剖分

圆锥曲线的统一定义

普通高中数学人教 A 版选修 2-1 P76

• 椭圆/双曲线准线：\(l: x=\pm\frac{a^2}{c}\)；抛物线准线：\(l: x=-\frac{p}{2}\)
  令曲线上一点到焦点和准线得距离分别为 \(d_F,~d_l\)，则有\(\frac{d_F}{d_l}=e\)，\(F,~l\) 同侧。

平分线

\(x\) 轴为角平分线的两边解析式关系

已知 \(l_1,~l_2\) 形成一个角，\(x\) 轴为这个角的角平分线，则有 \(k_1+k_2=0\)。

2

• \(\text{MN}\) 平分 \(\angle F_1MF_2\)，\(N\) 与 \(\text{F}_1\text{F}_2\) 共线。则有 \(\frac{\text{F}_1\text{N}}{\text{F}_2\text{N}}=\frac{\text{F}_1\text{M}}{\text{F}_2\text{M}}\)
  - 证明写了但是打起来太麻烦，以后再补
• 角平分线上的点到角两边的距离相等。
• 垂直平分线上的点到两端点的距离相等

Misc

• 在抛物线 \(y^2=2px\) 中，有 \(|\text{AB}|=|\text{AF}|+|\text{BF}|=|\text{A'D}|+|\text{B'E}|=x_A+x_B+p\)。其中 \(A,~B\) 在抛物线上，\(A',~B'\) 为 \(A,~B\) 在准线上的投影。
• 直线与双曲线的交点个数以渐近线斜率作为参考。

导数

通用操作

• 试根
  • \(x\in \mathbb{Z} \cap [-2,~2]\)
  • 根据式子试一些 \(e\) 的幂次：\(x=e^k,~k\in \mathbb{Z} \cap [-2,~2]\)
• 遇到 \(xe^x,~x\ln x\) 此类没法整掉就要考虑换方法了。
• 积化和：证 \(abcde\leq e^2\) 即证 \(\ln (abcde)\leq 2\)，即证 \(\ln a+\ln b+\ln c+\ln d+\ln e\leq 2\)，此化简方便求导之类的操作。

求 \(f(x)\geq 0\) 时 \(k\) 的范围

（2020·十堰模拟）已知 \(f(x)=axe^x-x^2-2x\)。当 \(x>0\) 时若曲线 \(f(x)\) 在 \(y=-x\) 上方，求 \(a\) 的取值范围。
本套路下即求 \(f(x)-(-x)\geq 0\)。

证明 \(k\) 在一定范围内有 \(f(x)\geq 0\) 建议使用下一节所述方法。

由 \(f(x)\geq 0\) 得到一个 \(a\geq g(x)\) 的方程。（如果不能分离出 \(a\) 这套路就没法用了）

然后通过 \(g'(x)=0\)（或 \(g''(x)=0\) 等，一般不超过二阶导）获得 \(g(x)\) 的极值。这里要运用导数分析一下。

然后就行了。

已知 \(k\) 的范围证明 \(f(x)>0\)

求证 \(a>\ln 2-1\) 且 \(x>0\) 时 \(e^x>x^2-2ax+1\)

这类题在 \(f(x),~f'(x),~f''(x)\) 的表达式中代入 \(a\) 的范围得到一个不等式，进行分析得证。

\(e^x>x^2-2ax+1\) 等价于 \(f(x)=e^x-x^2+2ax-1>0\)。

通过 \(f''(x)=0\) 发现在 \(x=\ln 2\) 时 \(f'(x)\) 取得最小值 \(2-2\ln 2+2a\)，代入 \(a\) 的范围得 \(f'(x)>0\)，即在定义域上单调递增，又因为 \(f(0)=0\)，得证。

求根相关

这一块主要是画图。画图找这几个点，连线：

• 求 \(f(x)\) 在定义域两端（包括 \(\pm \infty\)）的极限
• 求 \(f'(x)=0\) 时的 \(f(x)\)
• 求 \(f(x)\) 无定义时（例如 \(f(x)=\frac{1}{x-1}\)）在无定义点的左右极限
• \(y\) 截距。

1

已知 \(f(x)=3\ln x-\frac{1}{2}x^2+2x-3\ln 3-\frac{3}{2}\)，求 \(f(x)=0\) 的解的个数。

画图。看图就行了。

2

已知 \(f(x)=\ln x+\frac{k}{x}\)，讨论 \(g(x)=f'(x)-\frac{x}{3}\) 零点个数。

将 \(g(x)=0\) 变式成 \(k=h(x)\) 的形式。画 \(h(x)\) 的图。分别写出在各个 \(y=k\) 时与 \(h(x)\) 交点个数。
如果 \(h'(x)\) 很难算这个套路就不适用，看看下一个。

3

转换成一个等式，一边是一个不熟悉的不带参数的函数，另一边是熟悉的带参数的函数，把左边的图画出来，然后脑补右边参数各个取值与左边图的交点个数。

设 \(f(x)=x-\frac{1}{x}-2\ln x\)，讨论关于 \(x\) 的方程 \(x-\frac{1}{x}-f(x)=x^3-2ex^2+tx\)。

这个如果用上面的套路会解出 \(h'(x)=-8x^2+4ex-\frac{2}{x}\)（SOL-1），明显很毒瘤。

转化成 \(2\ln x=x^3-ex^2+tx\)，右边是三次函数，左边是将要变得毒瘤的式子，这类题只需要简化一边就行了。

同除 \(x\) 得 \((h(x)=\frac{2\ln x}{x})=x^2-ex+t\)，右边是个对称轴已经确定，没确定 \(y\) 截距的二次函数，左边的没有参数可以画出来。

然后恰好 \(h(x)\) 的极值点和右边的对称轴都是 \(e\)，脑补一下顶点在不同 \(y\) 时与 \(h(x)\) 的交点就行了。

4：证明区间上至多有一个零点

\(f(x)=\frac{x^2}{2}-k\ln x, k>0\)，证明若 \(f(x)\) 存在零点则 \((1,e]\) 上仅有一个零点。

这类题把极小值点的 \(x\)（一般含有参数 \(k\)）代入 \(f(x)\)，求 \(f(x)\leq 0\) 时 \(k\) 的范围，然后用这个范围简单分析一下就行了。

首先易得 \(x=\sqrt{k}\) 为 \(f(x)\) 的最小值点，\(x\rightarrow 0\) 及 \(x\rightarrow +\infty\) 时 \(f(x)\rightarrow +\infty\)。
当 \(f(x)\) 存在零点（即 \(f(\sqrt{k})\leq 0\)）时得 \(\sqrt{k}\geq \sqrt{e}\)，然后简单分析即可。

双变量

1

\(t(x)=f(x)-g(x)=x^2+(m-2)x-m\ln x-\frac{1}{2}x^2-m\ln x\)，令 \(x_1>x_2\)，有 \(\frac{t(x_1)-t(x_2)}{x_1-x_2}\geq m\) 恒成立，求 \(m\) 的范围。

化简得 \(t(x_1)-mx_1\geq t(x_2)-mx_2\)，令 \(h(x)=t(x)-mx\)，则可知 \(h(x_1)\geq h(x_2)\) 恒成立，即 \(h(x)\) 单调递增，即 \(h'(x)>0\) 在定义域上恒成立。

2

与上面那题方法类似，稍微综合一些。

已知 \(f(x)=\ln x+x^2+x,~f(x_1)+f(x_2)+x_1x_2=0\)，求证 \(x_1+x_2\geq \frac{\sqrt{5}-1}{2}\).

化简得 \((x_1+x_2)^2-2x_1x_2+x_1+x_2=-x_1x_2-\ln(x_1x_2)\)，即 \((x_1+x_2)^2+x_1+x_2=x_1x_2-\ln(x_1x_2)\)。

令 \(t=x_1x_2,~p=x_1+x_2\)，RHS 即 \(h(x)=t-\ln t\)，分析得 \(t\) 的范围，得 \(p^2+p\geq 1\)，即得 \(p\) 的范围。

即重点在于把两种形式分离，方便定义新函数。

交点相关

证 \(f(x),~g(x)\) 交点唯一 / 不存在

求导，求 \(f(x)-g(x)\) 极值和单调性，然后一波分析。

Misc

• \(g(x)=x^4y'+3x^3y=e^x\)，观察发现 \(\frac{g(x)}{x}\) 是 \(h(x)=x^3y\) 的导数。

坐标系与参数方程

坐标系

这一块主要是极坐标和直角坐标，有 \(x=\rho\cos\theta,~y=\rho\sin\theta,~\rho=x^2+y^2\)。

第一问转直角方程的话一般要把方程里转化到只剩下常数项、\(\rho\sin\theta\)、\(\rho\cos\theta\) 和 \(\rho^2\) 的常数倍。

第二问先尝试在极坐标下面算。

弦长最小

转化成弦心距最大。
在弦过定点时定点和圆心连线与弦垂直时弦心距最大，即弦长最小。

求 \(x+y\) 最大值

转化成参数方程求解。

同时出现 \(x\) 和 \(y\) 的待求式可以试试转为参数方程。

参数方程

• 直线参数方程中 \(|t|\) 表示从起点走的长度。过定点的直线用参数方程表示，代入直角方程求交点。距离操作例如 \(|MP|+|NP|\) 转化为 \(|t_1|+|t_2|\)。

注意求 \(x\) 的取值范围

画出来的图 \(x\) 不一定定义在 \(\mathbb{R}\) 上，一般参数为角度的转化成 \(A(\sin \alpha+\beta)\)。

\(x=\sqrt{3}\sin\alpha-\cos\alpha\)

\(x=2(\frac{\sqrt{3}}{2}\sin\alpha-\frac{1}{2}\cos\alpha)=2\sin(\alpha+\frac{\pi}{3})\Rightarrow x\in [-2,~2]\)

---

SageMath 算出来的解

SOL-1

\(\newcommand{\Bold}[1]{\mathbf{#1}}\left[x = -\frac{{\left(-i \, \sqrt{3} + 1\right)} e^{2}}{12 \, {\left(9 \, \sqrt{-\frac{2}{3} \, e^{3} + 9} + e^{3} - 27\right)}^{\frac{1}{3}}} - \frac{1}{12} \, {\left(i \, \sqrt{3} + 1\right)} {\left(9 \, \sqrt{-\frac{2}{3} \, e^{3} + 9} + e^{3} - 27\right)}^{\frac{1}{3}} + \frac{1}{6} \, e, x = -\frac{{\left(i \, \sqrt{3} + 1\right)} e^{2}}{12 \, {\left(9 \, \sqrt{-\frac{2}{3} \, e^{3} + 9} + e^{3} - 27\right)}^{\frac{1}{3}}} - \frac{1}{12} \, {\left(-i \, \sqrt{3} + 1\right)} {\left(9 \, \sqrt{-\frac{2}{3} \, e^{3} + 9} + e^{3} - 27\right)}^{\frac{1}{3}} + \frac{1}{6} \, e, x = \frac{e^{2}}{6 \, {\left(9 \, \sqrt{-\frac{2}{3} \, e^{3} + 9} + e^{3} - 27\right)}^{\frac{1}{3}}} + \frac{1}{6} \, {\left(9 \, \sqrt{-\frac{2}{3} \, e^{3} + 9} + e^{3} - 27\right)}^{\frac{1}{3}} + \frac{1}{6} \, e\right]\)

物理

电磁

• 多杆等效成并联

微积分理解

\(N\) 为线圈数，\(S\) 为横截面面积
电动势 \(\varepsilon=-\frac{\text{d}\Phi_B}{\text{d}t}\) （法拉第定律）
磁感应强度 \(B=\mu_0\frac{N}{l}I\Rightarrow\frac{\text{d}B}{\text{d}t}=\mu_0\frac{N}{l}\frac{\text{d}I}{\text{d}t}\)，其中 \(\mu_0\) 为磁导率，是一个常数。
磁通量 \(\Phi=NBS\Rightarrow\frac{\text{d}\Phi}{\text{d}t}=N(\frac{\text{d}B}{\text{d}t}\cdot S+\frac{\text{d}S}{\text{d}t}\cdot B)\)，这个在中学课本上以另一种形式出现了。

练习题：
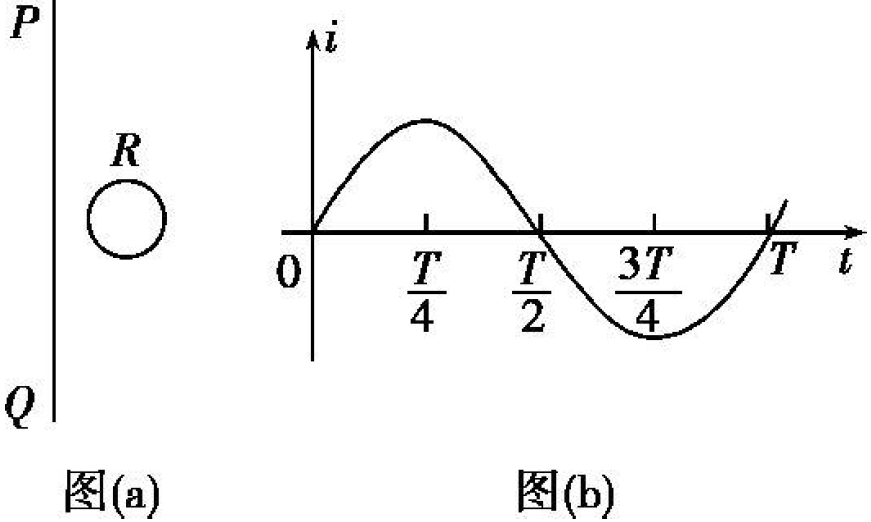
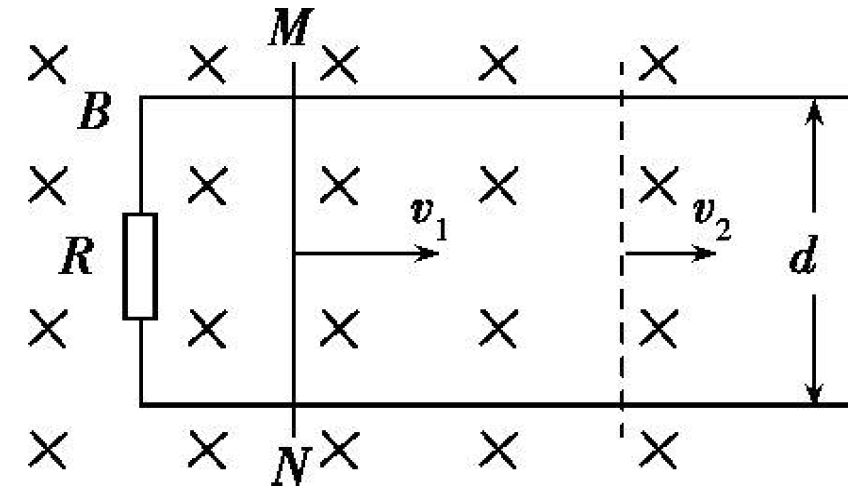
（2018·全国 III）(多选）20. 如图 (a)，在同一平面内固定有一长直导线 \(\text{PQ}\) 和一导线框 \(\text{R}\), \(\text{R}\) 在 \(\text{PQ}\) 的右侧。导线 \(\text{PQ}\) 中通有正弦交流电 \(i\), \(i\) 的变化如图 (b) 所示 , 规定从 \(Q\) 到 \(P\) 为电流正方向。导线框 \(R\) 中的感应电动势：
A. 在 \(t=\frac{T}{4}\) 时等于 \(0\)
B. 在 \(t=\frac{T}{2}\) 时改变方向
C. 在 \(t=\frac{T}{2}\) 时最大，且沿顺时针方向
D. 在 \(t=T\) 时最大，且沿顺时针方向

为了防止你不小心看到答案，对答案进行了编码。答案的 Base64 是 QUM=，请在这里解码。

电荷量

求时间 \(t\) 内经过电阻 \(R\) 的电荷量。

\[\begin{cases} Q=\bar It \\ \bar E=\frac{\Delta\Phi}{\Delta t}=\frac{B\Delta S}{\Delta t} \\ \bar I=\frac{\bar E}{R} \end{cases} \]

由上式得 \(Q=\frac{\frac{B\Delta S}{\Delta t}\cdot \Delta t}{R}=\frac{B\Delta S}{R}=\frac{\Delta \Phi}{R}\)

一道综合题

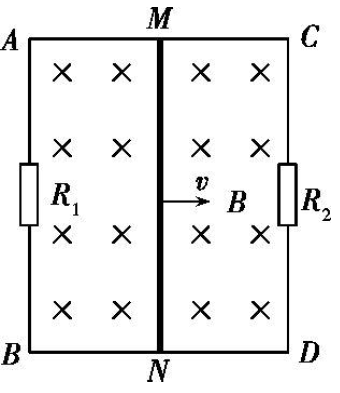
（2019·四川高中毕业班第二次诊断性考试）（多选）21. 如图所示，\(\text{AC}\) 与 \(\text{BD}\) 两平行金属导轨宽度 \(L=1~\text{m}\)，电阻不计且足够长。两端分别接有电阻 \(R_1=6~\Omega\) 和 \(R_2=3~\Omega\)。导体棒 \(\text{MN}\) 与 \(\text{AC},~\text{BD}\) 垂直，两端与导轨接触良好，电阻 \(r=1~\Omega\)，质量 \(m=1~\text{kg}\)，可在导轨上无摩擦滑动。垂直穿过导轨的匀强磁场磁感应强度为 \(B=1~\text{T}\)。现给 \(\text{MN}\) 一个初速度 \(v=0.3~\text{m/s}\)，沿平行 \(\text{AC}\) 边向右移动。下列说法正确的是：
A. 初始时 \(\text{MN}\) 加速度大小为 \(0.1~\text{m/s}^2\)
B. 整个过程中 \(R_1\) 上产生的热量为 \(0.020~\text{J}\)
C. 整个过程中通过 \(R_2\) 的电荷量为 \(0.1~\text{C}\)
D. \(\text{MN}\) 棒向右滑行的最大距离为 \(0.9~\text{m}\)

A

\[\begin{align} \nonumber \begin{cases} a&=\frac{F}{m}\\ F&=BIL\\ I&=\frac{E}{R}\\ E&=Blv \end{cases} \end{align} \]

得 \(a=\frac{(Bl)^2v}{mR}=0.1~\text{m/s}^2\).

B

由 \(Q=\frac{1}{2}mv^2\) 得 \(Q=0.045~\text{J}\)。
由 \(\frac{R_1}{R_2}=\frac{2}{1}\) 及 \(Q=\frac{E^2}{R}t\) 得 \(\frac{Q_1}{Q_2}=\frac{1}{2}\)，即 $Q_1=0.015~\text{J}。

C

由动量定理得 \(Ft=BL(It)=mv\)，即 \(BLq=mv\)，得 \(q=\frac{mv}{BL}=0.3~\text{C}\)。
由 \(q=It, \frac{I_1}{I_2}=\frac{1}{2}\) 得 \(q_2=0.2\text{C}\)。

D

\[\begin{align} \nonumber \begin{cases} \bar v&=\frac{x}{t}\\ \bar E&=Bl\bar v=Bl\frac{x}{t}\\ \bar I&=\frac{\bar E}{R_{\text{tot}}}=\frac{Bl\bar v}{R_{\text{tot}}}=\frac{Bl\frac{x}{t}}{R_{\text{tot}}}\\ q&=\bar It=\frac{Blx}{R_{\text{tot}}} \end{cases} \end{align} \\ \therefore x=\frac{QR_{\text{tot}}}{Bl}=9~\text{m} \]

化学

以下标题带 * 的内容由 Aluminum_铝 支持，无特殊声明版权由他所有，转载请联系他进行授权。

铝哥哥太强啦！

1 硫酸根不做氧化剂 *

结构上来说，硫酸根正电荷中心被牢牢锁在 \(\mathrm{[SO_4]}\) 四面体笼里，所以说高中认为只有浓硫酸才有氧化性，氢的存在破坏了电子结构的稳定性，但是离子态没得办法，所以高中老师说稀硫酸不具有氧化性。

2 *

将用烧碱吸收 \(\mathrm{H_2S}\) 所得的溶液进行电解，阳极区发生如下反应：
\(\mathrm{S}^{2-}-2\mathrm{e}^-=S,~(n-1)\mathrm{S}+\mathrm{S}^{2-}=\mathrm{S}_n^{2-}\)
稀硫酸酸化阳极区电解产物得到硫单质，写出其离子方程式。

从命题上来说，这道题其实是歧化归中条件猜测的玩法。在高中常见的环境下是酸利于归中，碱利于歧化，本质因为不少阴离子只有在碱性下才能稳定存在。

这道题如非要硬套酸归中碱歧化简易规中的话是套不出来的，就只有回归本质，就是在浓碱溶液中 \(\mathrm{S}_n^{2-}\) 缔合离子会稳定。

前置知识很多？其实也没有，只要你看得懂那个信息，就是只有浓碱条件下稳定存在。那这道题就能往回倒推，酸性条件下它不稳定，那就把他打回原形就可以了。

升降价态配平

1

1 标价态升降

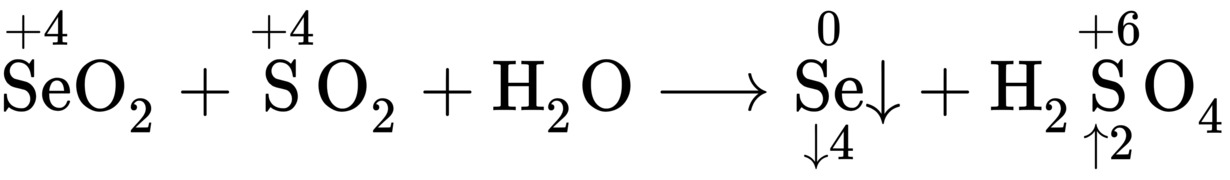
2 按升降比例配一侧

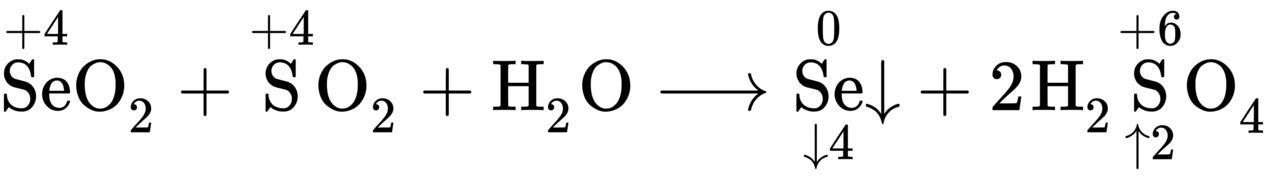
3 原子守恒、（离子方程式）电荷守恒

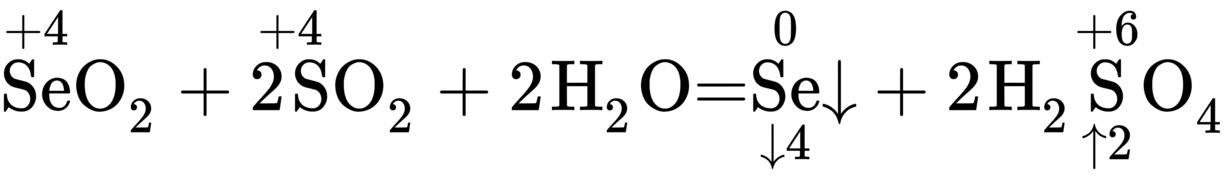
2

已知 \(\text{FeS}_2\) 与 \(\text{MnO}_2\) 反应生成 \(\text{S},~\text{MnO4},~\text{Fe}_2(\text{SO}_4)_3\)，求化学反应方程式。

生物

• AO （相对于 AA, Aa 等） 表示染色体缺失