一题的双坐标系解法

Problem

如图所示，四边形 \(ABCD\) 是直角梯形，\(AD\parallel BC\)，\(AD\bot CD\)，\(\angle ABC=\frac{\pi}{3}\)，\(BC=2AD=2\)，\(PC=3\)，\(\triangle PAB\) 为等边三角形. 求证 \(AB\bot PC\).

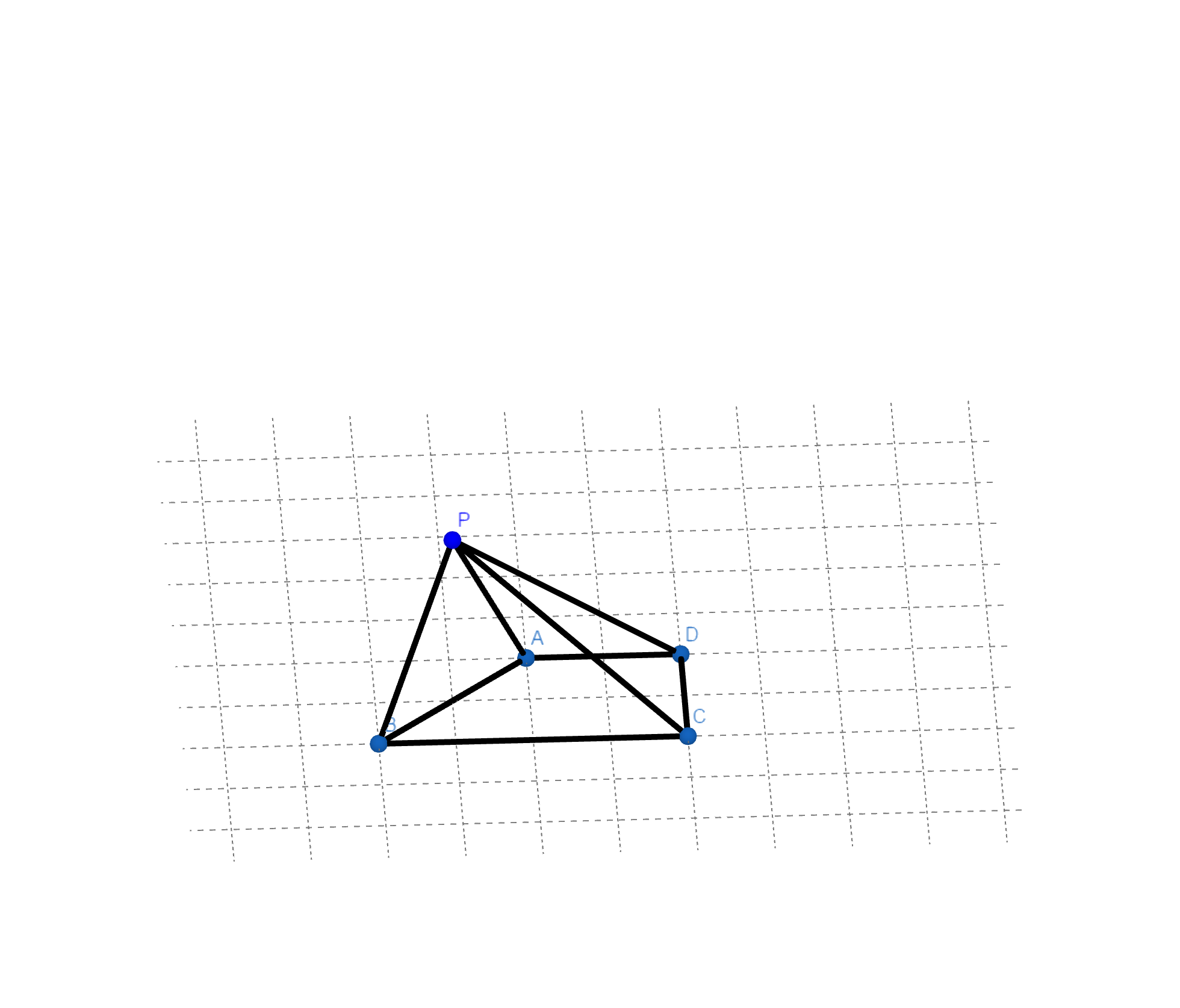
Solution

这题显然有很简单的方法，但是我从学空间向量开始就想尝试两个坐标系一起用，终于找到一题。

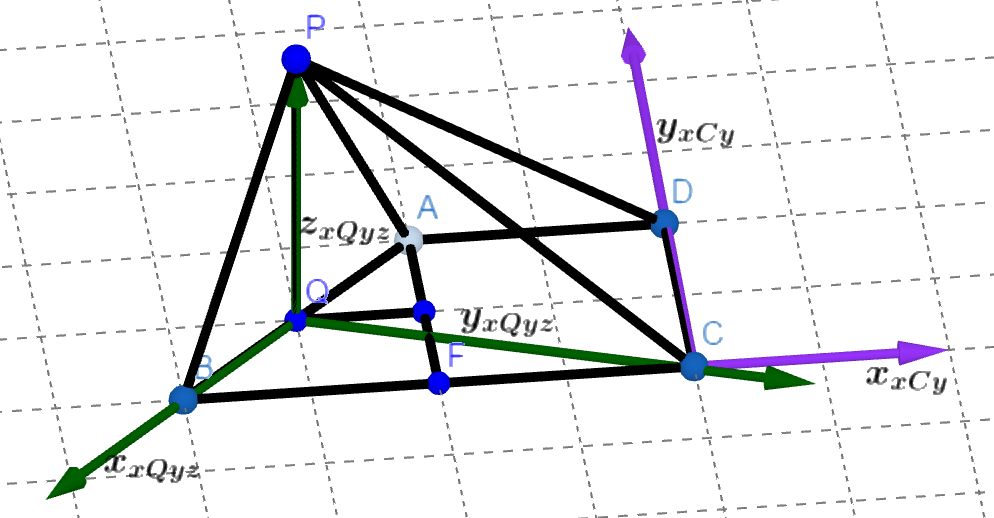
图中 \(F\) 就是 \(P_2\)，为了把所有元素画出来，生成图的时候视角有点奇怪。

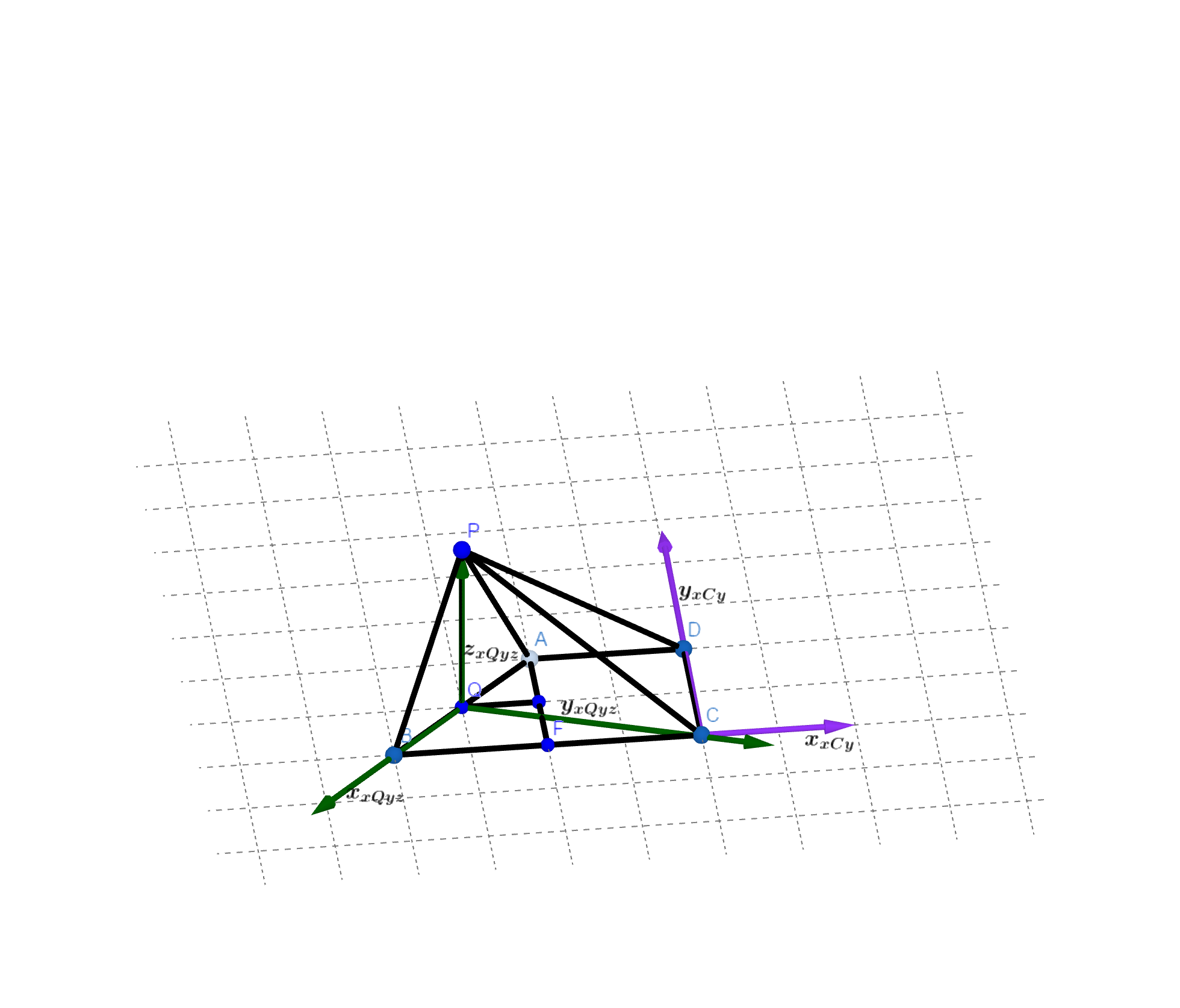
做 \(AP\bot BC\) 于点 \(P_2\)，\(PQ\bot AB\) 于点 \(Q\)。

这里 \(P_2\) 原来是 \(P\) 但是忘了原图已经有个 \(P\) 点了这样加下标比较顺手就加上了。

\(\because AP\parallel BC,\ AD\bot CD,\ AP_2\bot BC\)
\(\therefore \angle APC=\angle ADC=\frac{\pi}{2},\ AP_2\parallel DC,\ AD\parallel PC\)
\(\therefore\) 四边形 \(ADP_2C\) 为矩形
\(\therefore AD=P_2C=1\)
又 \(\because BC=BP_2+CP_2\)
\(\therefore BP_2=1\)
又 \(\because \angle ABC=\frac{\pi}{3}\)
\(\therefore AB=2,\ AP_2=\sqrt{3}\)
又 \(\because \triangle PAB\) 是等边三角形，\(PQ\bot AB\)
\(\therefore PQ=\sqrt{3}\)
连接 \(QC\)，以 \(C\) 为原点，\(CD\) 为 \(x\) 轴正方向建立平面直角坐标系 \(xCy\)
在 \(xCy\) 中有：
\(A(-1,\sqrt{3}),B(-2,0),C(0,0),D(0,\sqrt{3}),Q(\frac{-1-2}{2},\frac{\sqrt{3}}{2})=(-\frac{3}{2},\frac{\sqrt{3}}{2})\)
则 \(BC=2,\ BQ=1,\ QC=\sqrt{{(-\frac{3}{2})}^2+{(-\frac{\sqrt{3}}{2})}^2}=\sqrt{3}\)
\(\because BC^2=BQ^2+QC^2\)，由勾股定理逆定理得 \(\angle BQC=\frac{\pi}{2}\)
\(\therefore BQ\bot QC\)
又 \(\because PQ\bot BA\)
\(\therefore\) 以 \(Q\)为原点，\(QB\)为 \(x\) 轴正方向，\(QC\) 为 \(y\) 轴正方向建立空间直角坐标系 \(xQyz\)
在 \(xQyz\) 中有：
\(C(0,\sqrt{3},0),P(0,0,\sqrt{3}),B(1,0,0),A(-1,0,0)\)
\(\therefore \vec{PC}=(0,\sqrt{3},0),\vec{AB}=(2,0,0)\)
\(\therefore \vec{PC}\cdot \vec{AB}=0\)
\(\therefore PC\bot AB\)