智能账单统计软件开发日志3 图像比对算法

Part A - 预处理

预处理有，分析出联通块和文字区域

联通块分析

这个是个很简单的操作，因为之前已经把图像数据读入 vector 中了，但实际操作时有些问题。
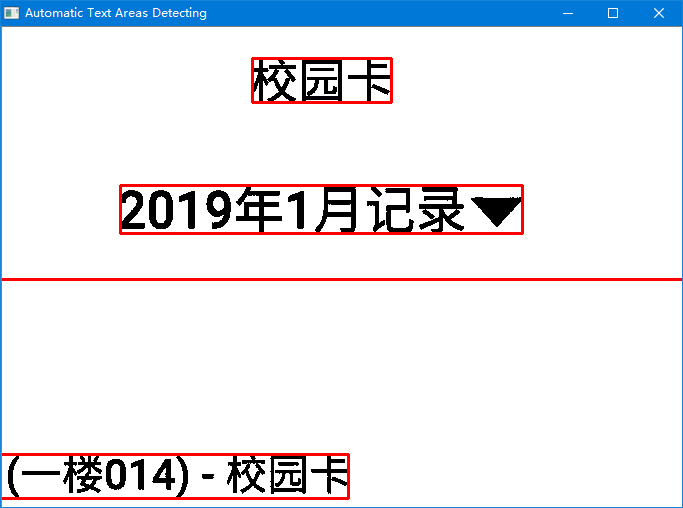
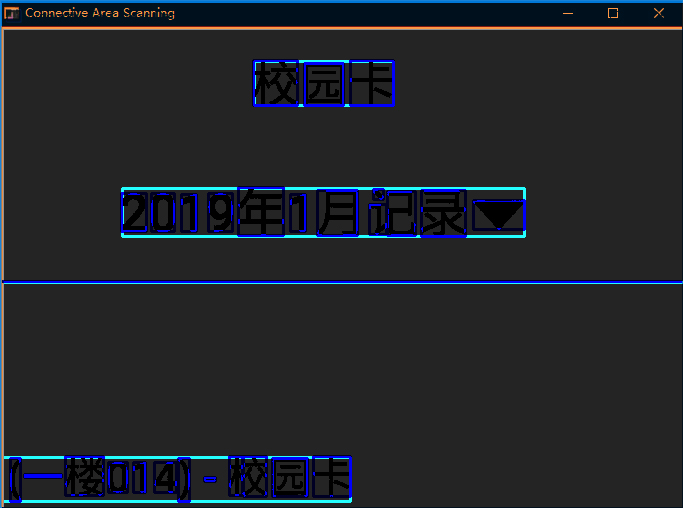
一个就是，此处“联通块”的定义和一般定义不同，此处“联通块”的目的是找出各个字符所在区域，因此需要去除包含的联通块情况，如下图所示，上面的是未处理，下面的是处理后。

其实，这里最优的操作是再做一遍小的形态学开操作，因为汉字是由几个部件构成的，这些部件中间有些空隙，不一定能搜的出来，但是这里只是为了让返回的结果漂亮一些，所以没有必要这样做，如果要分析出每个字，是要做开操作的。
第二个，因为 OpenCV、显示设备、C++ 一般调用方法 arr[x][y] 之间对坐标记录方法的差异，造成了 \(x,y\) 坐标对横纵的对应的混乱，造成数组越界，具体如下。
之前已经说过，因为不知道用户输入的大小，所以使用了 vector 嵌套。在做手动移除时，系统将坐标等值传入函数 on_remove_mouse，但是此时传入的是显示器坐标，即使用 \(x\) 横 \(y\) 纵的表示方法，而 OpenCV 与上述一般调用方法使用的是 \(x\) 纵 \(y\) 横的表示方法，因为写程序时间紧张，因此直接按 on_remove_mouse 的写法写了，但运行时会收到系统发出的 SIGTRAP 信号而停止。经了解， SIGTRAP 信号是收到断点时的操作。进行错误分析：

• 考虑 vector 受到空间限制

不可能：因为：

1. 当发生内存溢出错误时没有受到限制的表现
2. 传统内存限制通过编译错误报告（静态数组）
3. 使用小图片测试，故障依旧，但是但图片小到一定程度时，返回 Segment Fault
4. 尝试去除向 vector 进行 push_back 语句，故障依旧

• 考虑越界访问
  已知数组越界会发出 Segment Fault 报告，未尝试 vector 的越界，检查代码 + GDB print 操作调试、故障点上下各 printf 一次测试代码是否完成发现 \(x,y\) 弄反。

文字区域探测

一般来说，形态学的开操作做一次就可以得到非常不错的结果了，其中OpenCV 的 getStructuringElement 提供了一种非常简便的生成指定形状矩阵的方法。
在进行开操作后，再算一次连通块就行了，这次的图像信息和 vis 信息不用保留，直接 imgdata.clear()。

2019.11.9更新
形态学开操作会损失像素导致联通块存在但是文字区域不存在，但同时此操作可以消除较小噪点（几个像素）对文字区域检测的影响。

以下是结果，第二张是对两张图片做了一下叠加。

---

小提示：以下文章公式较多且繁复，如您觉得公式太小，可右键公式，依次点击第二项 (Math Settings) 的第一项 (Zoom Trigger) 里的第一项 (Hover)，这样当您把光标放到公式上面时，公式会自行放大。

Part B 图像比对

概述

经过研究，决定采用通过用户取样数字 0~9，小数点，正负号的方式，然后进行计算。
计算时如果使用对位比较显然不是一个好方法，因为如果使用这种方法，不能保证每一位都是相同的，因为在图像输入（如扫描）、形态调整（例如 jpeg 格式中的失真导致的像素点颜色值不真实，从而导致边缘粗糙）过程中不可避免的有不同数字的不同形态。因此，经过查找资料，使用 SSIM 结构相似性判断算法。在使用时，存在特例，例如将 - 在 . 模式下比较时，会将 - 直接变成近似 .，因此增加一个新的比较因素，按长宽比比较。

SSIM

SSIM 算法是一个衡量算法相似度的指标，其从亮度、对比度和结构三个方面对图像相似度进行评估，其还可通过比较压缩前后图像相似度评估压缩质量。
因为该算法要求等大小图像，因此通过对图像进行缩放来进行处理。为最小化失真，全部使用大图像缩成小图像的方法。

缩放原理

最基础的缩放算法缩放的原理是提取子块，并将其按比例缩放成新图像。如果是小图放成大图，那么就是一个像素点的颜色值放到 \(\frac{n}{N}\times \frac{m}{M}\) 个元素中去，其中 \(n,m\) 为新图片的长宽，\(N,M\) 为旧图片的长宽。例如将一个 \(2\times 2\) 的图片放大成 \(8\times 8\) 的图片。如果是大图缩成小图，那么就是某个区域取均值（再进行二值化）后放到对应的格子里。

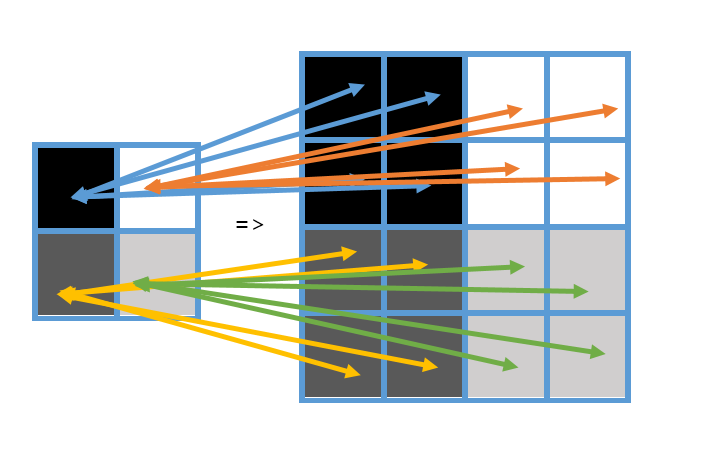
在 OpenCV 中已经提供了 resize 函数，直接调用即可。

---

以下内容来源于参考资料 1
该函数不同于朴素算法，其提供了多种插值方式用于优化图像处理后的结果，其选择如下：

INTER_NEAREST - 最近邻插值
INTER_LINEAR - 线性插值（默认）
INTER_AREA - 区域插值
INTER_CUBIC - 三次样条插值
INTER_LANCZOS4 - Lanczos插值

---

其中三次样条差值需要 \(4\times 4\) 的采样区域，Lanczos 差值需要 \(8\times 8\) 的采样区域\(^{[1]}\)，对于样本和待求图这类较小的图像不太适合。

根据 OpenCV 文档，缩小图片时 INTER_AREA 有较好的效果，放大图片时使用 INTER_CUBIC（慢） 和 INTER_LINEAR（快，能看）效果较好。
对于本例来说，需要注重图片上的细节，因此使用放大，对图片放大的系数不大，使用线性插值。

To shrink an image, it will generally look best with INTER_AREA interpolation, whereas to enlarge an image, it will generally look best with c::INTER_CUBIC (slow) or INTER_LINEAR (faster but still looks OK).

SSIM 的计算\(^{[2]}\)

首先先要计算出两个图片的均值，方差和协方差：
均值：\(\mu _X=\frac{\sum ^R_{i=1}\sum ^C_{j=1}X(i,j)}{R\times C}\)，这个很好理解，就是求算术平均数。
方差：\(\sigma _X=\sqrt{\frac{\sum ^R_{i=1}\sum ^C_{j=1}(X(i,j)-\mu _X)^2}{R\times C-1}}\)，也是一般的方差求法。
协方差：\(\sigma _{XY}=\sqrt{\frac{\sum ^R_{i=1}\sum ^C_{j=1}(X(i,j)-\mu _X)(Y(i,j)-\mu _Y)}{R\times C-1}}\)，即用两个图中同一位置与对应图像平均值的差的乘积取代原方差算法，也就是其为什么叫做协方差，协同计算方差。

然后运用这些值，衡量两个图亮度 \(L\) (Lighting)，对比度 \(C\) (Contrast)，结构 \(S\) (Struct) 之间的相似度，相乘即得到整体相似度。
其中，\(L(X,Y)=\frac{2\mu _X\mu _Y+C_1}{\mu _X^2+\mu _Y^2+C_1}\)，\(C(X,Y)=\frac{2\sigma _X\sigma _Y+C_2}{\sigma _X^2+\sigma _Y^2+C_2}\)，\(S(X,Y)=\frac{\sigma _{XY}+C_3}{\sigma _X\sigma _Y+C_3}\)。
这里面的 \(C_1,C_2,C_3\) 均为常数，为防止除零错误所用，一般取 \(C_1=(K_1\times L)^2,C_2=(K_2\times L)^2,C_3=\frac{C_2}{2}\)，其中 \(K_1=0.01, K_2=0.03, L=255\)，\(L\) 为像素值的动态范围，一般取 \(255\)。
此时可得 \(SSIM(X,Y)=L(X,Y)\times C(X,Y)\times S(X,Y)\)，在上述常数定义下，\(SSIM(X,Y)=\frac{(2\mu _X\mu _Y+C_1)(2\sigma _{XY}+C_2)}{(\mu _X^2+\mu _Y^2+C_1)(\sigma _X^2+\sigma _Y^2+C_2)}\)。

因素调节

在 \(L,C,S\) 三个值上乘上系数调节它们对结果影响的比例。在程序实现中，二值化后只关注结构上的相似度，因此直接返回 \(S\) 值。

2019/11/24 更新
增加读取样本数据功能时发现，由于使用的是 mat.at<uchar>(x,y) 取出图像上的点，因此样本图像也必须是在黑白灰度空间下的。

总结

生活处处皆数学，在这看似直观的图像中，隐藏着无尽的数学奥秘。计算机视觉其实就是用数学给计算机戴上一副眼镜，让它和人一样能够领略世间万物的美好。

参考资料
1: OpenCV(3)-图像resize，作者 Korbin
2: 图像质量评估算法 SSIM(结构相似性)，作者 chaibubble