一道微分方程题

Problem

\(\frac{3y^2+1}{y^3+y}\cdot \frac{\text{d}y}{\text{d}x}=2x,~y(0)=1\)，求 \(y=4\) 时 \(x\) 的值。

Solution

1

\[\int \frac{3y^2+1}{y^3+y}~\text{d}y=x^2+C \]

2

\[\begin{align} \int \frac{3y^2+1}{y^3+y}~\text{d}y & = \int \frac{3y^2+3-2}{y(y^2+1)}~\text{d}y\nonumber\\ & = \int \frac{3}{y}~\text{d}y-\int \frac{2}{y(y^2+1)}~\text{d}y\nonumber\\ & = 3\ln |y|-\int \frac{2}{y(y^2+1)}~\text{d}y\nonumber \end{align} \]

3

简化 \(\int \frac{2}{y(y^2+1)}~\text{d}y\)。

\[\nonumber \begin{align} \frac{A}{y}+\frac{By+C}{y^2+1}=\frac{2}{y(y^2+1)}\nonumber\\ Ay^2+A+By^2+Cy=2\nonumber \end{align} \]

得 \(A+B=0,~C=0,~A=2\)，即 \(A=2,~B=-2,~C=0\)。
即

\[\begin{align} \int \frac{2}{y(y^2+1)}~\text{d}y&=\int\frac{2}{y}~\text{d}y-\int\frac{2y}{y^2+1}~\text{d}y\nonumber\\ &=2\ln |y|-\int\frac{2y}{y^2+1}~\text{d}y\nonumber \end{align} \]

3.1

简化 \(\int\frac{2y}{y^2+1}~\text{d}y\)。

令 \(u=y^2+1\)，则 \(\text{d}u=2y\)，即 \(\int\frac{2y}{y^2+1}~\text{d}y=\int \frac{1}{u}~\text{d}u=\ln u=\ln (y^2+1)\)

4

综合以上各式，得 \(3\ln |y|-2\ln |y|+\ln(y^2+1)=x^2+C\)。
代入 \(x=0,~y=1\) 得 \(C=\ln 2\)。
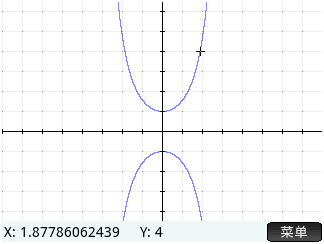
代入 \(y=4\) 得 \(x=\sqrt{\ln 4+\ln 17-\ln 2}=\sqrt{\ln \frac{4\cdot 17}{2}}=\sqrt{\ln{34}}\)

Graph