统计学习方法五 决策树分类

决策树分类

1，概念

　　　　

　　　　

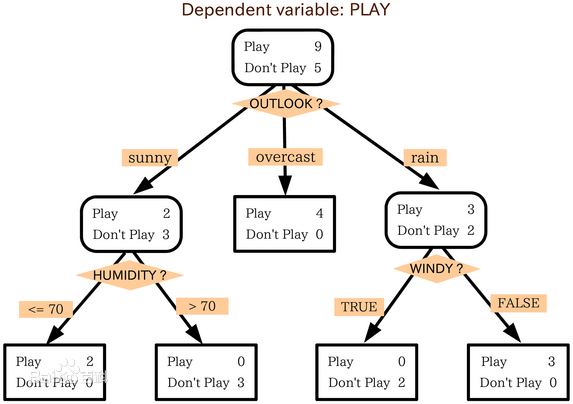
2，决策树算法

2.1，特征选择：

　　熵：值越大，不确定性因素越大；条件熵：即已知x存在的情况下求y的不确定性（越小越好）；信息增益（互信息）：熵减去条件熵（度量了X在知道Y以后不确定性减少程度），越大越好；

　　　　

　　　　　　　　　　　　

　　　　　　　

 

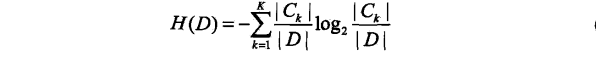
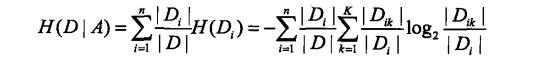
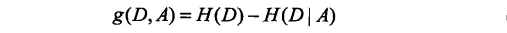
2.2，决策树生成算法

1，ID3算法

　　

　　

2，c4.5算法

　信息增益率等于：g(D,A)/H(A),为什么要用信息增益率，实例引用http://blog.csdn.net/zjsghww/article/details/51638126：

　　　　　　1，id3算法对某个特征的属性值数多有偏好性（所以适合离散性属性集），如主键ID，其H(D,ID)=0，即其g(D,ID)最大，但用主键ID去划分显然没什么效果，所以C4.5通过添加1/H(A)作为惩罚因子，如ID,该值为1/log2n<1,对g(D,A)有惩罚作用

　　　　　　2，增益率准则对属性取值较少的时候会有偏好，为了解决这个问题，C4.5并不是直接选择增益率最大的属性作为划分属性，而是之前先通过一遍筛选，先把信息增益低于平均水平的属性剔除掉，之后从剩下的属性中选择信息增益率最高的，这样的话，相当于两方面都得到了兼顾。

　　

伪代码：

伪代码：
输入：训练数据集D，特征集合A
输出：决策树T
方法 Generate_decision_tree(D,A):
（1）创建结点N
（2）if D属于同一类别C，return N做为叶结点，C为类标记
（3）if A等于空，return N做为叶结点，值C为D中最多的类别数
（4）选择A中信息增益（信息增益率）最大的特征Ai,标记N结点内容为Ai的值
（5）foreach Ai中的每个属性值Aij,将原先的训练集D划分为Dj,特征集A等于A-Ai中的每个属性值Aij
（6）递归调用Generate_decision_tree(D,A)
//可以设置阈值来进一步进行筛选，但需要人为设置

3，实例说明

　　

          　 

                                

                             

                           

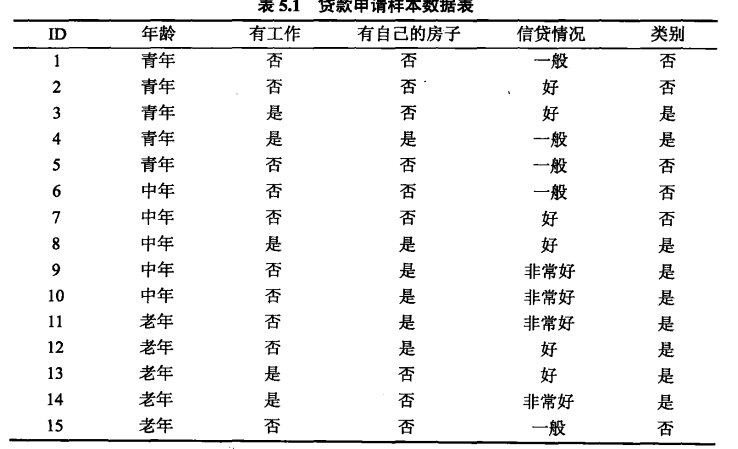
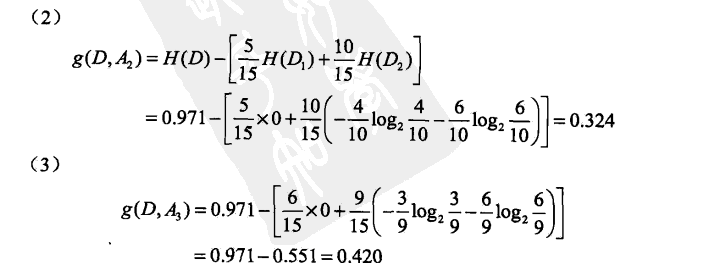
4，CART决策树算法

                 

4.1 决策树生成

　回归树生成

　　　注意点：为了使最小化最小二乘回归值（实际值减预测值）等价于

，所以让预测值为平均值时结最小二乘回归值最小，来选择最优切分点。针对连续性变量是小于等于该切分点，和大于该切分点两大块

　            

　　回归伪代码：

输入：训练数据集D，停止条件e
输出：回归树T
方法 CART_regression_tree(D,e)
（1）创建结点N
（2）if 满足条件return N N的值为D中的平均值
（3）遍历每个特征j,对每个固定的切分变量j扫描切分点s,通过公式来计算出最优切分点s，将数据集D划分为Ds1和Ds2，N的值为最优切分变量j和切分点s
（4）递归调用CART_regression_tree（Ds1,e)和CART_regression_tree(Ds2,e)
//条件e可以是D中数量小于某中程度或最小误差小于e等类似的情况
// 步骤（3）中遍历特征需要注意，根据离散特征分支划分数据集时，子数据集中不再包含该特征
（因为每个分支下的子数据集该特征的取值就会是一样的，信息增益或者Gini Gain将不再变化）；
而根据连续特征分支时，各分支下的子数据集必须依旧包含该特征（当然，左右分支各包含的分别是取值小于、大于等于分裂值的子数据集），
因为该连续特征再接下来的树分支过程中可能依旧起着决定性作用。

http://www.jianshu.com/p/b90a9ce05b28

分类树生成

　　        

             

                

                     

                          

CART分类伪代码：
输入：训练数据集D，停止条件e
输出：分类树T
方法 CART_classification_tree(D,e)
（1）创建结点N
（2）if 满足条件（可以是D中数量小于某中程度或基尼指数小于e等类似的情况) return N N的值为D中的众数
（3）遍历每个特征j,对每个固定的切分变量j扫描切分点s,通过公式计算求出最优切分点s，将数据集D划分为Ds1和Ds2，N的值为最优切分变量j和切分点s
（4）递归调用CART_classification_tree（Ds1,e)和CART_classification_tree(Ds2,e)
（5）生成决策分类树T

// 步骤（3）中遍历特征需要注意，根据离散特征分支划分数据集时，子数据集中不再包含该特征
（因为每个分支下的子数据集该特征的取值就会是一样的，信息增益或者Gini Gain将不再变化）；
而根据连续特征分支时，各分支下的子数据集必须依旧包含该特征（当然，左右分支各包含的分别是取值小于、大于等于分裂值的子数据集），
因为该连续特征再接下来的树分支过程中可能依旧起着决定性作用。
//对连续属性处理优化方法：对特征的取值进行升序排序，优化算法就是只计算分类属性发生改变的那些特征取值

　　　举个例子：

 　　　　

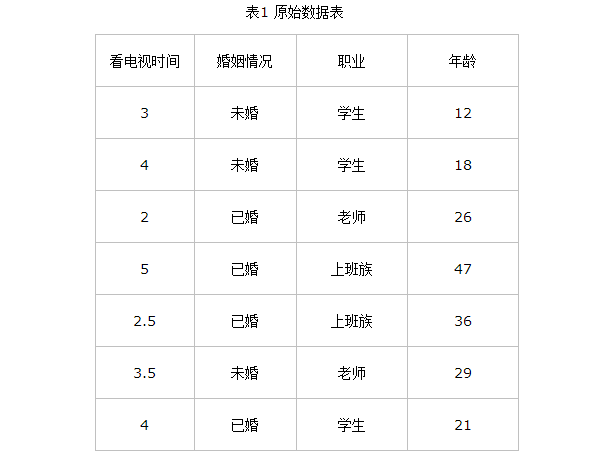
 　　　　第一种划分方法：{“学生”}、{“老师”、“上班族”} 来预测婚姻

　　　　　　　　

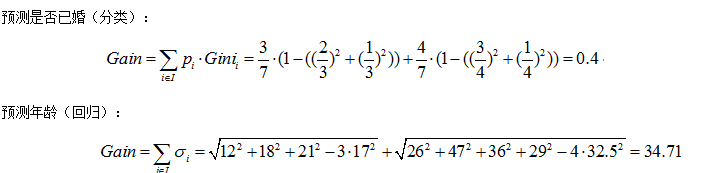
　　　　第二种划分方法：{“老师”}、{“学生”、“上班族”}

                           

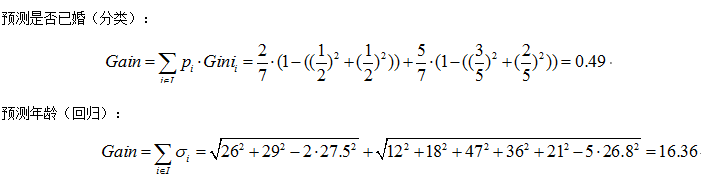
　　　　第三种划分方法：{“上班族”}、{“学生”、“老师”}

                        

4.2，决策树剪枝

　　　　代价复杂度剪枝（ccp）

        　　

 

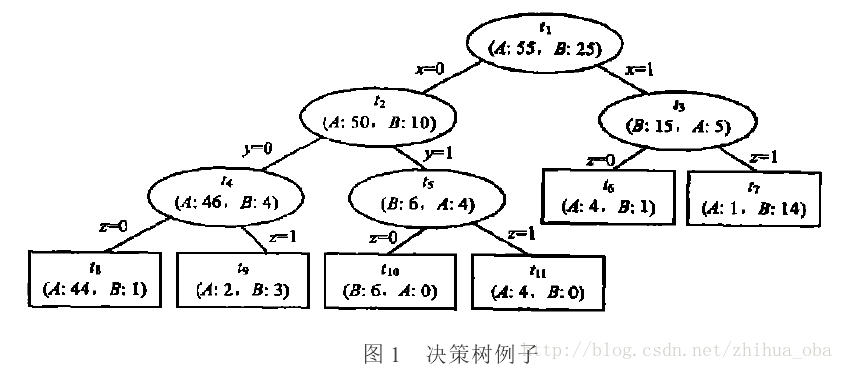
　　　　例如：图1中ti表示决策树中第i个节点，A、B表示训练集中的两个类别，A、B之后的数据表示落入该节点分别属于A类、B类的样本个数。 

 　　　　　　　　

　　　

5，决策树算法比较

　　  

6，总结

　　个人认为算法通过使用训练集构建一个决策树后，获得一系列的规则，输入测试集后，按照规则获取到叶节点，然后根据叶节点最大占有比的那个类为该测试集所属的类，从而达到分类效果

　　决策树可以认为是将空间进行划分，ID3和C4.5算是比较经典的决策树算法，可以用来分类，也可以用来回归，但业界很少直接使用一棵树，一般使用多棵树，组成committee，较为经典有GBDT 和RF，两者都是ensemble learning的典范，只不过前者使用boosting降低bias，后者使用bagging降低variance从而提升模型的performance。在ESL中有个对比，使树形模型几乎完爆其他算法，泛化能力和学习能力都很牛逼。业界的话一般用来做搜索排序和相关性。

 

 

参考网址：

　　1，cart例子

　　1.1，决策树对离散数据和连续性数据的处理方法

　　2，剪枝例子

　　3，决策树比较