KMP算法思路
题目
给定一个字符串\(S\),求\(M\)字符串是否是\(S\)字符串中的子串.如果是,返回\(M\)对应\(S\)的第一个下标,否则返回-1.
例如:S串为a b c d a b c d a b c d e
M串为a b c d e
结果:返回S串下标8.
个人想法
之前看过这种求子串的题,但是只在脑海中想象了一下,没有动手写出算法.
看到的时候心里就嘀咕肯定不能暴力求解,需要让子串\(M\)进行跳跃,但是没有具体地研究边界问题,也没有动手写一个字符串验证想法,导致想法很不靠谱.
之前的想法很粗糙:
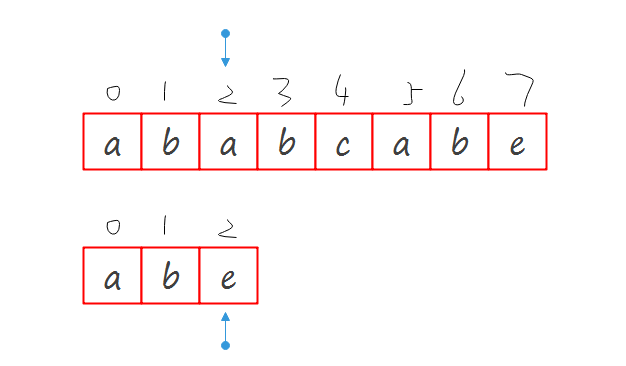
挨个比较字符串,如果不相同,整体都跳跃,跳跃的方式是\(M\)串首位对其不匹配\(S\)串的下标位置.然后继续比较
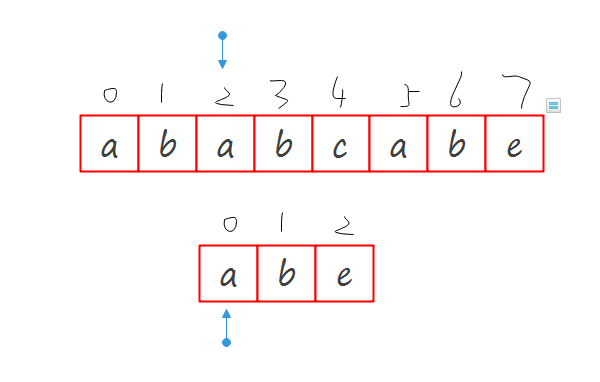
大约就是这个样子,想到这就没继续往下想也没有去实现,这显然是错误的.跳跃是应该跳跃,但是不是那么粗糙的跳跃,假如字符串和子串是下面这种情况这种情况:
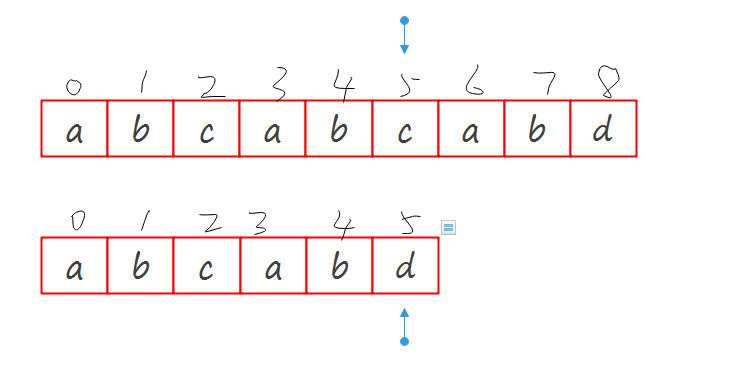
以我那种错误的想法是会产生bug的:
结果是\(S\)串不会包含\(M\)串,但事实上是包含的.(下文将目标串统一称作\(S\),子串统一称作\(M\))
那我们就应该考虑如何正确的跳跃.
KMP算法
知道了之前的想法是错误的,我们就应该找到符合各种边界的跳跃方式.只要确定了跳跃方式,KMP就很容易写出来了.KMP中提到了前缀表(或者最大相同前后缀)这些概念.前缀表暂时先不考虑,只谈谈如何进行跳跃才能满足边界.
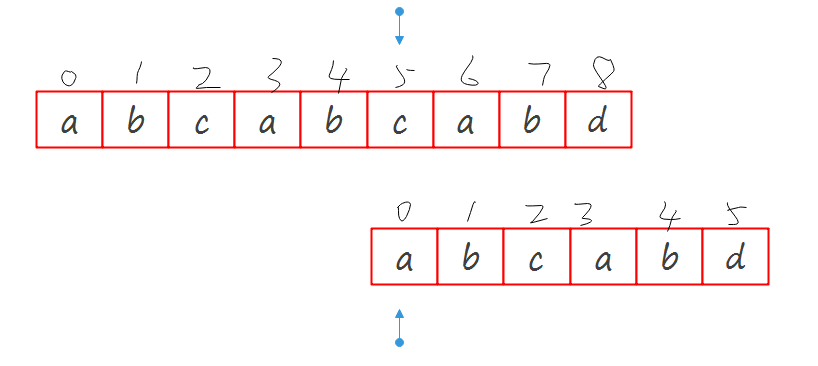
继续回到之前的图,如果我们想要成功地找到下标,正确的跳跃方式应该是下图这样:
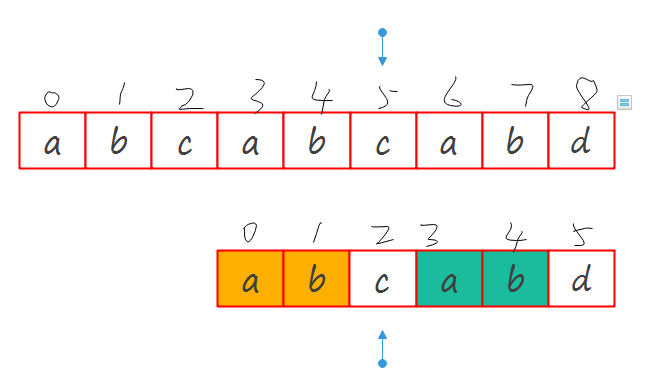
注意\(M\)串错误匹配项(\(M[5]\)元素d)之前的元素(蓝色填充的a,b).
好,为什么这么跳呢?
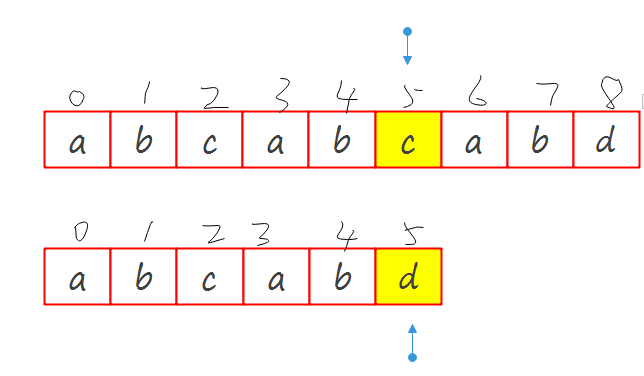
当确定\(S[5]\)和\(M[5]\)不匹配的时候,我们可以确定d之前的项都是匹配的.即\(S[0-4]\)和\(M[0-4]\)是匹配的.
\(M[0-4]\)
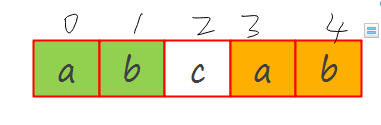
对于已经匹配的\(M[0-4]\),前缀几项与后缀几项相同(即\(M[0]\),\(M[1]\)和\(M[3]\),\(M[4]\)是相同的),那么把\(M\)平移使\(M[0]\)对齐\(M[3]\)之前所处的位置,这一定能确保\(M[0]\),\(M[1]\)和之前\(M[3]\),\(M[4]\)与\(S\)对应的\(S[3]\),\(S[4]\)是匹配的,即一定能确保\(M[0]\),\(M[1]\)和\(S[3]\),\(S[4]\)是匹配的.
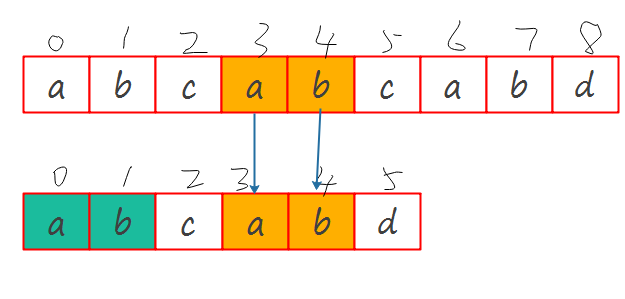
平移
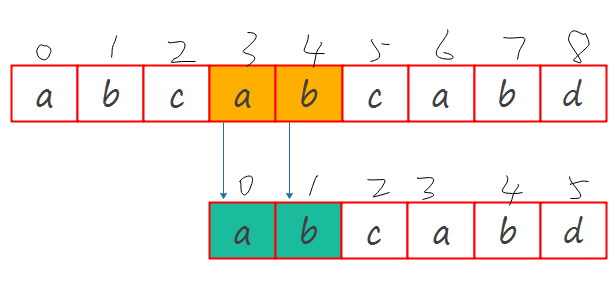
那我们如何利用这个特点跳跃呢,现在我们生成一个辅助的前后缀相同的数组.
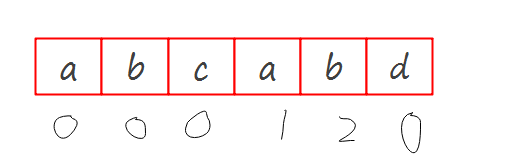
以a,b,c,a,b,d为例,
| M产生的子串 | 相同前后缀个数 | 备注:就把相同前后缀数组称为\(D\) |
|---|---|---|
| a | 0 | |
| a,b | 0 | |
| a,b,c | 0 | |
| a,b,c,a | 1 | |
| a,b,c,a,b | 2 | |
| a,b,c,a,b,d | 0 | 最后一个匹配就可以返回了,所以用处不大 |
最后生成一个相同前后缀的数组可以与\(M\)对应起来
现在只需要解释一下如何使用相同前后缀数组进行跳跃,应该就能写出KMP的代码了.
当\(M[5]\)与\(S[5]\)不相同时,看一下前后缀数组\(D\)前一个位置的值,即\(D[4]\)的值为2,那么只需要将\(M[2]\)平移至\(M[5]\)的位置上就可以了.如果\(M[3]\)不匹配,后缀数组\(D\)的前一位\(D[2]\)是0,那么就把\(M[0]\)平移对其\(M[3]\)的位置就可以了.
假如\(M[0]\)不匹配的话,就直接往后跳一位,与\(S\)下一项比较.
KMP代码实现(JAVA)
整体思路就大致如此了,如果理解了应该可以按照思路写出代码了.
下面就贴一下代码实现,我只是简单地测试了一下,没有大量测试,但是整体思路应该大致如此,可能有些边界问题还没有考虑周全,欢迎指正.
public static int getIndexOf(String s, String m) {
if (s == null || m == null || m.length() < 1 || s.length() < m.length()) return -1;
char[] ss = s.toCharArray(), ms = m.toCharArray();
int si = 0, mi = 0;
int[] next = getMatchArray(ms);
int q = next[mi];
while (si < ss.length && mi < ms.length) {
if (ss[si] == ms[mi]) {
si++;
mi++;
} else {
if (mi != 0) {
mi = next[mi - 1];
} else {
si++;
}
}
}
return mi == ms.length ? si - mi : -1;
}
public static int[] getMatchArray(char[] ms) {
if (ms.length == 1) return new int[]{0};
int[] next = new int[ms.length];
next[0] = 0;
int j = 0, tail = 1;
while (tail < ms.length) {
j = next[tail] = ms[j] == ms[tail] ? (j + 1) : 0;
tail++;
}
return next;
}
public static void main(String[] args) {
String str = "abcabcababaccc";
String match = "ababa";
System.out.println(getIndexOf(str,match));
}

