dfs序
1.定义
dfs序:每个节点在dfs深度优先遍历中的进出栈的时间序列
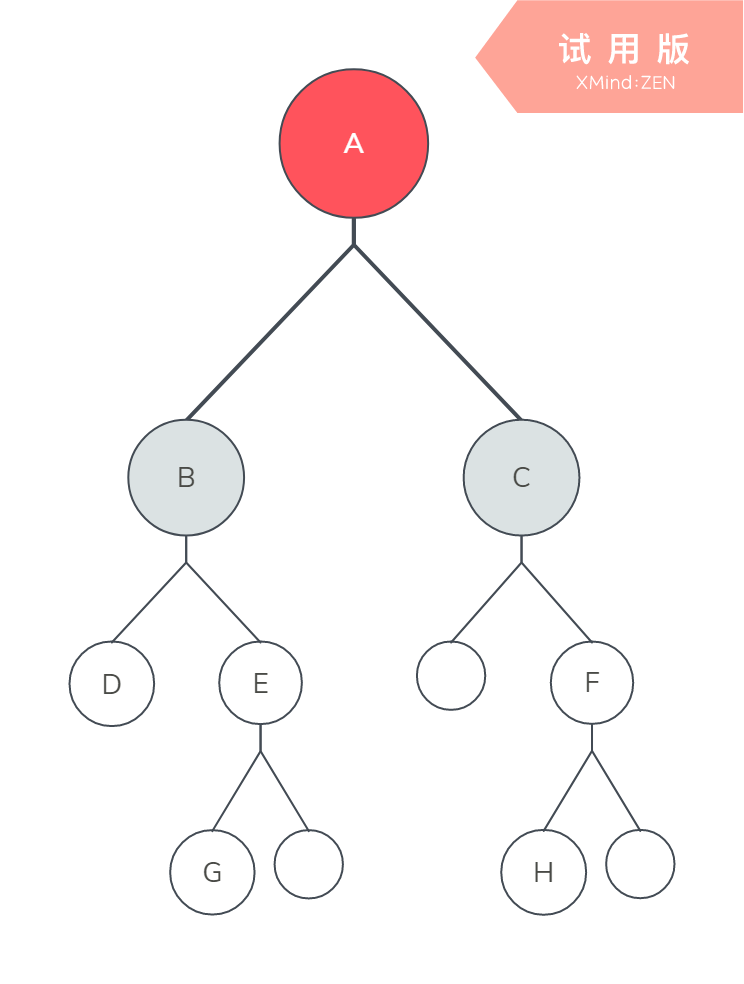
dfs序就是A-B-D-D-E-G-G-E-B-C-F-H-H-F-C-A
2.性质

为了便于理解,我们举个example
我们都知道它的dfs序A-B-D-D-E-G-G-E-B-C-F-H-H-F-C-A
我们可以发现B的出入栈时间点之间的是B的子树
因为搜索进下一个点时时间增加,且结束时间逐级传递。
所以说我们的点的子节点的时间区间一定包含在这个点的时间区间内。
所以如果一个点的起始时间和终结时间被另一个点包括,这个点肯定是另一个点的子节点。(简称括号化定理)
也就是说,子树的dfs序肯定大于根节点的进栈时间小于根节点的出栈时间,这就成了一个区间问题。所以我们就把一个树上的问题“拍”到了一个线性的数据结构上面。区间问题就可以用线段树、树状数组、splay...各种优秀的算法解决了
3.时间戳
时间戳记录第一次开始访问这个点的时间和和最后结束访问的时间
void dfs(int node,int parent){
NewIdx[NCnt] = node;
InOut[NCnt] = 1;
InIdx[node] = NCnt++;
for(int next=Vertex[node];next;next=Edge[next].next){
int son = Edge[next].to;
if ( son != parent ) dfs(son,node);
}
NewIdx[NCnt] = node;
InOut[NCnt] = -1;
OutIdx[node] = NCnt++;
}
dfs序求lca
点u,v的LCA还满足它是其中一个点的最近的一个祖先,满足u,v都在它的子树中。
判断一个点是否在另一个点的子树中,我们可以用dfs序来判断。
这是倍增的另一种判断方法:
void dfs(int p, int fa) {
bz[p][0] = fa, in[p] = ++cnt;
for (int i = 1; i < bzmax; i++)
bz[p][i] = bz[bz[p][i - 1]][i - 1];
for (int i = g.h[p]; ~i; i = g[i].nx) {
int e = g[i].ed;
if (e == fa) continue;
dfs(e, p);
}
out[p] = cnt;
}
int lca(int a, int b) {
if (dep[a] > dep[b]) swap(a, b);
if (in[a] <= in[b] && out[a] >= out[b])
return a;
for (int i = bzmax - 1, nx; ~i; i--) {
nx = bz[a][i];
if (!(in[nx] <= in[b] && out[nx] >= out[b]))
a = nx;
}
return bz[a][0];

简单的模板题
从前有一棵以1为根的有根树,
树的每个节点有一个权值。
现在请你维护如下操作:
1、令节点x的权值增加y
2、询问以节点x为根的子树中所有节点的权值和。
一眼题,dfs序把树上问题转化为区间问题,然后线段树单点修改,区间查询
还是简单的模板体
树的每个节点有一个权值。
现在请你维护如下操作:
1、将以节点x为根的子树中所有节点的权值增加y
2、询问节点x的权值。
操作变成区间修改,单点查询
普通的模板体
从前有一棵以1为根的有根树,
树的每个节点有一个权值。
现在请你维护如下操作:
1、将从节点x出发到节点y路径上的所有节点权值增加z。
2、询问节点x的权值。
一道裸的树链剖分题,还有什么方法可以解决呢?
这个操作等价于
a. 对X到根节点路径上所有点权加W
b. 对Y到根节点路径上所有点权加W
c. 对LCA(x, y)到根节点路径上所有点权值减W
d. 对LCA(x,y)的父节点 father(LCA(x, y))到根节点路径上所有权值减W
于是要进行四次这样从一个点到根节点的区间修改
将问题进一步简化, 进行一个点X到根节点的区间修改, 查询其他一点Y时
只有X在Y的子树内, X对Y的值才有贡献且贡献值为W
于是只需要更新四个点, 查询一个点的子树内所有点权的和即可
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
const int MAXN = 1e5+10;
vector<int> edge[MAXN];
int s[2*MAXN];
int seq[2*MAXN];
int seq1[2*MAXN];
int depth[2*MAXN];
int first[MAXN];
int dp[2*MAXN][25];
int st[MAXN];
int ed[MAXN];
int parent[MAXN];
int cnt, num;
int Lowbit(int x)
{
return x & (-x);
}
void Add(int x, int val, int n)
{
if(x <= 0) return;
for(int i = x; i <= n; i += Lowbit(i)) {
s[i] += val;
}
}
int Sum(int x)
{
int res = 0;
for(int i = x; i > 0; i -= Lowbit(i)) {
res += s[i];
}
return res;
}
void Dfs(int u, int fa, int dep)
{
parent[u] = fa;
seq[++cnt] = u;
seq1[++num] = u;
first[u] = num;
depth[num] = dep;
st[u] = cnt;
int len = edge[u].size();
for(int i = 0; i < len; i++) {
int v = edge[u][i];
if(v != fa) {
Dfs(v, u, dep+1);
seq1[++num] = u;
depth[num] = dep;
}
}
seq[++cnt] = u;
ed[u] = cnt;
}
void RMQ_Init(int n)
{
for(int i = 1; i <= n; i++) {
dp[i][0] = i;
}
for(int j = 1; (1 << j) <= n; j++) {
for(int i = 1; i + (1 << j) - 1 <= n; i++) {
int a = dp[i][j-1], b = dp[i + (1 << (j-1))][j-1];
dp[i][j] = depth[a] < depth[b] ? a : b;
}
}
}
int RMQ_Query(int l, int r)
{
int k = 0;
while((1 << (k + 1)) <= r - l + 1) k++;
int a = dp[l][k], b = dp[r-(1<<k)+1][k];
return depth[a] < depth[b] ? a : b;
}
int LCA(int u, int v)
{
int a = first[u], b = first[v];
if(a > b) a ^= b, b ^= a, a ^= b;
int res = RMQ_Query(a, b);
return seq1[res];
}
void Init(int n)
{
for(int i = 0; i <= n; i++) {
edge[i].clear();
}
memset(s, 0, sizeof(s));
}
int main()
{
int n, op;
int u, v, w;
int cmd;
while(scanf("%d %d", &n, &op) != EOF) {
Init(n);
for(int i = 0; i < n-1; i++) {
scanf("%d %d", &u, &v);
edge[u].push_back(v);
edge[v].push_back(u);
}
cnt = 0, num = 0;
Dfs(1, -1, 0);
RMQ_Init(num);
while(op--) {
scanf("%d", &cmd);
if(cmd == 0) {
scanf("%d %d %d", &u, &v, &w);
int lca = LCA(u, v);
Add(st[u], w, cnt);
Add(st[v], w, cnt);
Add(lca, -w, cnt);
Add(parent[lca], -w, cnt);
}
else if(cmd == 1) {
scanf("%d", &u);
printf("%d\n", Sum(ed[u]) - Sum(st[u] - 1));
}
}
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号