自动化技术中的进给电气传动-读书笔记3
1.3时间域描述
1.3.1
微分方程用来描述物理传递环节和系统的数学模型。
微分方程可以在一直输入量和边界条件的情况下计算出有关的输出量。


首先概括出物理规律性,然后建立起工作原理框图,推导出不可调传动系统的微分方程。
经过一系列的变换就可以得到不可调电气传动系统的二阶微分方程。

假定ML = 0,就可以解微分方程确定输出电压变化时的基准相应特性。
阶跃响应特性:
用来描述一个传递环节或一个系统的输出量在输入量发生一次阶跃式变化时的随时间变化过程。 可用来调节技术特性,
将微分方程简化:

在线性系统情况下。齐次的部分解描述系统动态部分,而特解则描述静止状态。两部分解之和就产生总解。
齐次部分解可以求出
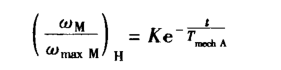
非齐次的部分解:

则微分方程的解为:
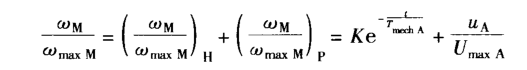
进而得出

可以看出,一个不可调传动系统的角速度Wm或转速Nm,在阶跃式接入电枢电压ua之后,按带有机械时间常数TmechA的指数函数形式变化。(前提无负载启动、电气时间常数TelA可忽略)

除了阶跃函数之外,还有另外两种在时间域中描述传递环节特性的方法。上升斜坡响应特性和单位脉冲响应特性,这些方法在传动技术中没有多大意义。
1.4复变量域描述
主要包括频率响应特性和伯德图。频率响应特性指的就是函数F(jw),伯德图是利用对频率响应特性绝对值以及对相位角的描述,得到的一个形象直观的线性传递环节的传递特性图。也可以说成,传递环节的幅值响应特性和相位响应特性。两者共同构成了伯德图。
特征角频率:特征角频率代替延迟时间或者特征值(对于P-T1环节和P-T2环节)
W0 = 1/T
谐振角频率:在谐振角频率时频率响应特性达到一个最大值。
Wr = W0*sqrt(1-2D^2)
固有角频率:系统的固有角频率是对时间域中瞬态响应特性的一个判断依据。
Wd = w0*sqrt(1-D^2)
1.5根轨迹
人们将极点在闭环系统的复数p平面中的几何位置称之为根轨迹曲线。
控制系统设计
控制系统:一般控制系统可以分为控制器和被控机器。
控制器:由控制律与功率变换器协同工作。
被控机器:由被控对象与反馈装置。
拉普拉斯变换:
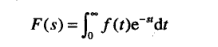
式中,函数f(t)是一个时间函数,s是拉警拉斯算子,而F(s)是变换函数。拉普拉斯变化和其反变换实现时间域和频率域之间的变换
频率域传递函数把两个信号之间的关系描述为一个关于s的函数。
s就是拉普拉斯算子,是个复变量。
频率域传递函数只限于描述线性、时不变性。
均一性和叠加性是关于线性化的。
控制器单元的传递函数:
- 积分和微分
- 滤波器
- 补偿器:补偿器是一种特殊的滤波器。是用来在某个频率提供特定增益与位移的滤波器,它对高于和低于该频率的信号的增益与相位的影响是次要的。
- 延迟:延迟不改变幅值。
反馈电路的简化,机械控制基础学过,有点遗忘,还需要补一补。
增益:用来测量输入和输出的幅值之间的差异,它通常用dB表示。
增益=20xlg(出幅/入幅)
相位 = -360 x F x tDELTA
心得难点:复变域还是比较好理解的,但对微分方程没有很好理解,有种不知所云的感觉。对于控制系统这本书, 频率域传递函数只限于描述线性、时不变性。不是很理解时不变性,看不懂在说什么。
其次概念还是比较多的,而且知识点环环相扣,所以理解的比较慢。


