z-score Normalization

　　Z-score 表示一个值是高于或低于平均值多少个标准差（ a score that indicates how many standard deviations a value is above or below the mean).

比如用于RNA-seq 的normalisation. 对每个基因的原始表达量减去平均基因丰度，然后除以所有样本测量的标准差SD(standard deviation) 。这个与TPMs(Transcripts per million)：计数通过特征长度归一化。

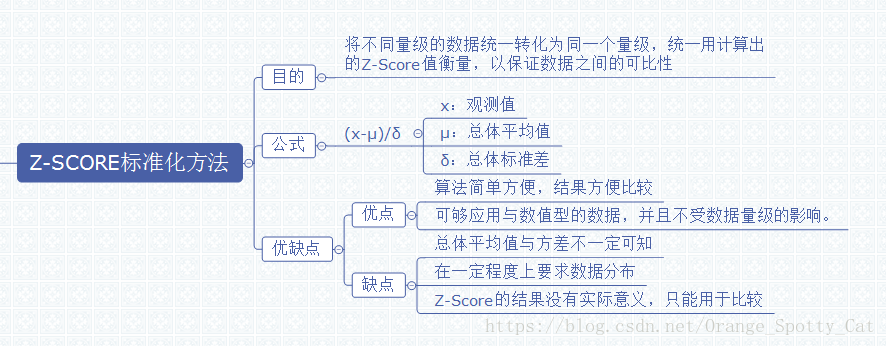
z-score主要目的将不同量级的数据统一转化为同一量级，统一用计算出的Z-score衡量，保证数据之间的可比性。计算之前需要：

　 1）总体数据的均值（μ）

　2）总体数据的标准差(σ)

　3) 个体的观测值(x)　　

计算(x-μ)/σ，实现将不同的数据转换到相同的量级上，值没有量纲，实现标准化。z score告诉我们这个值距离平均值相差几个标准差。

z-score = 1 意味着样本值超过均值 1 个标准差；
z-score = 2 意味着样本值超过均值 2 个标准差；
z-score = -1.8 意味着样本值低于均值 1.8 个标准差。
z-score告诉我们样本值在正态分布曲线中所处的位置。z-score = 0告诉我们该样本正好位于均值处，z-score = 3 则告诉我们样本值远高于均值

参考： https://blog.csdn.net/qq_39482438/article/details/110873346

Normalization:

　　standard deviation(SD): 衡量一组变量的离散程度。低标准差表示变量很接近mean平均值，然而高的的标准差表示值离散到更广的范围, 总体标准差(population standard deviation)用lower case Greek letter σ (sigma)表示，样本标准差用Latin letter s表示。随机变量、样本、统计分布、数据集、概率分布的标准差是方差的平方根。相比方差，它与数据样本的单位相同。

　　总体或样本的standard deviation 与统计量的standard error（如样本均值 sample mean）不同，但相关。样本均值的standard error 是从总体中抽取无限量的重复样本并计算每个样本的standard deviation，来找到均值集的标准偏差(standard deviation). 均值的standard error 等于总体standard deviation除以样本量的方根，是用样本standard deviation除以样本量的平方根来估计。

在科学研究中，会同时说明数据的standard deviation作为summary statistic,以及估计的standard error作为研究中潜在错误的衡量方法。按照惯例，距离零期望（null expectation）两个standard errors以外的效应才被认为是显著，

例子