区间DP专题

区间DP是通过小区间来转移从而取得大区间得结果；

[CQOI2007]涂色

题目描述

假设你有一条长度为 \(5\) 的木板，初始时没有涂过任何颜色。你希望把它的 \(5\) 个单位长度分别涂上红、绿、蓝、绿、红色，用一个长度为 \(5\) 的字符串表示这个目标：\(\texttt{RGBGR}\)。

每次你可以把一段连续的木板涂成一个给定的颜色，后涂的颜色覆盖先涂的颜色。例如第一次把木板涂成 \(\texttt{RRRRR}\)，第二次涂成 \(\texttt{RGGGR}\)，第三次涂成 \(\texttt{RGBGR}\)，达到目标。

用尽量少的涂色次数达到目标。

输入格式

输入仅一行，包含一个长度为 \(n\) 的字符串，即涂色目标。字符串中的每个字符都是一个大写字母，不同的字母代表不同颜色，相同的字母代表相同颜色。

输出格式

仅一行，包含一个数，即最少的涂色次数。

样例 #1

样例输入 #1

AAAAA

样例输出 #1

1

样例 #2

样例输入 #2

RGBGR

样例输出 #2

3

提示

\(40\%\) 的数据满足 \(1\le n\le 10\)。

\(100\%\) 的数据满足 \(1\le n\le 50\)。

思路：

1）从小区间开始看，len=1，f[l][r]=1
2) s[l]==s[r] f[l][r]=min(f[l+1][r],f[l][r-1])，意思就是，l和r得颜色相同，那么第一次可以把l到r都涂成一种颜色，所以不需要花费
3）s[l]!=s[r] 这时候就是区间之间需要合并，先枚举分界点，f[l][r]=min(f[l][k]+f[k+1][r])

代码：

#include <bits/stdc++.h>
#define int long long
int _ = 0, Case = 1;
using namespace std;
#define all(v) begin(v),end(v)
#define nline '\n'
const int N = 110;
int f[N][N];
char s[N];
void solve(int Case) {
    int n;
    cin >> (s + 1);
    n = strlen(s + 1);
    memset(f, 0x3f, sizeof f);
    for (int len = 1;len <= n;len++) {
        for (int l = 1;l + len - 1 <= n;l++) {
            int r = l + len - 1;
            if (len == 1) {
                f[l][r] = 1;
                continue;
            }

            if (s[l] == s[r]) {
                f[l][r] = min(f[l][r - 1], f[l + 1][r]);
            }
            else {
                for (int k = l;k <= r - 1;k++) {
                    f[l][r] = min(f[l][r], f[l][k] + f[k + 1][r]);
                }
            }
        }
    }
    cout << f[1][n] << nline;


}
signed main() {

    ios::sync_with_stdio(false); cin.tie(nullptr);
    //   for (cin>>_, Case = 1; Case <= _; Case++)
    solve(Case);
    return 0;
}

凸多边形的划分：

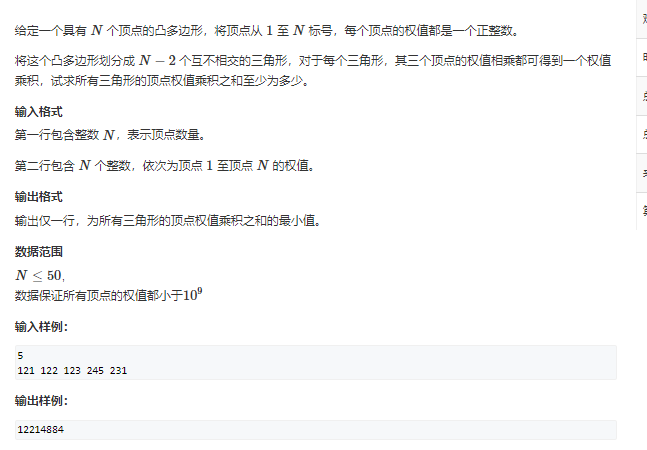
思路：

可以观察到长度为3的时候为 \(a[l]*a[r]*a[l+1]\)
长度为4时：\(min(f[l+1][r]+a[l]*a[r]*a[l+1],f[l][r-1]+a[l]*a[r]*a[r-1])\)
其他长度时：找一个分界点k，\(f[l][r]=min(f[l][k]+f[k][r]+a[l]*a[r]*a[k])\)

代码：

n=int(input())
a=list(map(int,input().split()))
a=[0]+a
f=[[0 for i in range(n+1)] for i in range(n+1)]
for len in range(3,n+1):
    for l in range(1,n-len+2):
        r=l+len-1
        f[l][r]=1<<100
        for k in range(l+1,r):
            f[l][r]=min(f[l][r],f[l][k]+f[k][r]+a[l]*a[r]*a[k])
        
print(f[1][n])