Atcoder Begnner Contest 253 (E,F)

E - Distance Sequence

思路：

考虑动态规划，前i项以j结尾的个数，第i-1项一定是上一项结尾小于等于j-k的个数+上一项结尾大于等于j+k的个数

代码：

#include <bits/stdc++.h>
#define int long long
int _ = 0, Case = 1;
using namespace std;
#define all(v) begin(v),end(v)
#define nline '\n'
 
const int N = 1010, M = 5 * N, mod = 998244353;
int f[N][M];
int s[N];
void solve(int Case) {
    int n, m, k;
    cin >> n >> m >> k;
    for (int i = 1; i <= m; i++) f[1][i] = 1;
    for (int i = 1; i <= m; i++) f[1][i] += f[1][i - 1];
    for (int i = 2; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            int low = j - k;
            int up = j + k;
            if (up == low) up++;
            if (low >= 0)
                f[i][j] =(f[i][j]+ f[i - 1][low])%mod;
            f[i][j] %= mod;
            if (up <= m)
                f[i][j] =(f[i][j]+ (f[i - 1][m] - f[i - 1][up - 1]+mod)%mod)%mod;
            f[i][j] %= mod;
        }
        for (int j = 1; j <= m; j++) {
            f[i][j] += f[i][j - 1];
            f[i][j] %= mod;
        }
    }
    cout << f[n][m] << nline;
 
 
 
 
}
 
signed main() {
    ios::sync_with_stdio(false); cin.tie(nullptr);
//   for (cin>>_, Case = 1; Case <= _; Case++)
    solve(Case);
 
    return 0;
}

F - Operations on a Matrix

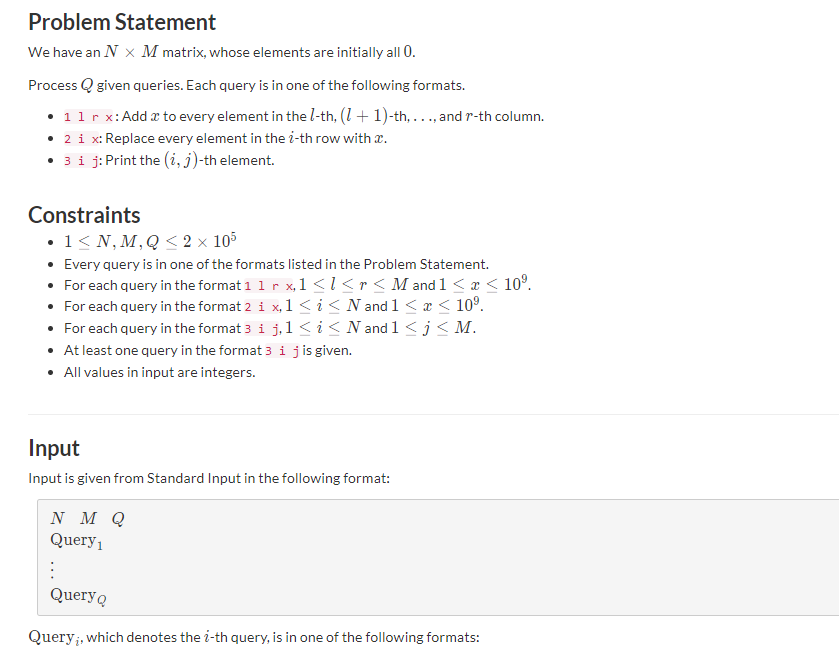
思路：

求操作3时，可以计算出第j列累加的值s，第i行最后一次变的值x，还有变成x的时候第j列累加的值s1，结果就是x+s-s1，使用离线做法

代码：

#include <bits/stdc++.h>
#define int long long
int _ = 0, Case = 1;
using namespace std;
#define all(v) begin(v),end(v)
#define nline '\n'
#define lowbit(x) x&(-x)
const int N = 2000010;
int c[N];
void add(int x, int y) {
    for (; x < N; x += lowbit(x)) c[x] += y;
}
int ask(int x) {
    int res = 0;
    for (; x; x -= lowbit(x)) res += c[x];
    return res;
}
struct T {
    int  val, sum;
    map<int, int> mp;
} pro[N];
struct TT {
    int opt, a, b, c;
} query[N];
int lst[N];
void solve(int Case) {
    int n, m, q;
    vector<T> v;
    cin >> n >> m >> q;
    for (int i = 1; i <= q; i++) {
        int op;
        cin >> op;
        if (op == 1) {
            int l, r, x;
            cin >> l >> r >> x;
            query[i] = {1, l, r, x};
            continue;
        } else if (op == 2) {
            int a, b;
            cin >> a >> b;
            lst[a] = i;
            query[i] = {2, a, b, 0};
        } else if (op == 3) {
            int a, b;
            cin >> a >> b;
            int p = lst[a];
            pro[p].mp[b] = 0;
            query[i] = {3, a, b, 0};
        }
    }
    for (int i = 1; i <= q; i++) {
        auto [op, a, b, c] = query[i];
        if (op == 1) {
            add(a, c), add(b + 1, -c);
        } else if (op == 2) {

            pro[i].val = b;
            lst[a] = i;
        } else {
            int s = ask(b);
            int p = lst[a];
            
            int s1 = pro[p].mp[b];
            int x = pro[p].val;
            cout << x + s - s1 << nline;
        }
        auto &mp = pro[i].mp;
        for (auto &[x, v] : mp) {
            v = ask(x);
        }
    }

}

signed main() {
    ios::sync_with_stdio(false); cin.tie(nullptr);
//   for (cin>>_, Case = 1; Case <= _; Case++)
    solve(Case);

    return 0;
}