camp div1每日一题
T1题意:
求每个区间的最大值减最小值的和
思路:
预处理出每个值作为他所在的区间中的最大值和最小值的贡献,然后求和相减,使用单调栈可以处理在每个值最多可以在那个区间中作为最值;
代码:
//枚举每个值在它的区间种的贡献
#include <bits/stdc++.h>
#define int long long
int _= 0, Case = 1;
using namespace std;
#define all(v) begin(v),end(v)
#define nline '\n'
const int N=5000010;
int a[N],l[N],r[N];
int n;
void cal1(){
stack<int> s;
a[0]=1e18;
s.push(0);
for(int i=1;i<=n;i++){
while(s.size()>1 and a[s.top()]<=a[i]) s.pop();
l[i]=s.top();
s.push(i);
}
}
void cal2(){
stack<int> s;
a[n+1]=1e18;
s.push(n+1);
for(int i=n;i>=1;i--){
while(s.size()>1 and a[s.top()]<a[i]) s.pop();
r[i]=s.top();
s.push(i);
}
}
void cal3(){
stack<int> s;
a[0]=0;
s.push(0);
for(int i=1;i<=n;i++){
while(s.size()>1 and a[s.top()]>=a[i]) s.pop();
l[i]=s.top();
s.push(i);
}
}
void cal4(){
stack<int> s;
a[n+1]=0;
s.push(n+1);
for(int i=n;i>=1;i--){
while(s.size()>1 and a[s.top()]>a[i]) s.pop();
r[i]=s.top();
s.push(i);
}
}
void solve(int Case) {
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
}
cal1(),cal2();
int sum=0;
for(int i=1;i<=n;i++){
int x=a[i];
int lenl=i-l[i];
int lenr=r[i]-i;
sum+=(lenl*lenr)*x;
}
int sum1=0;
for(int i=1;i<=n;i++) l[i]=r[i]=0;
cal3(),cal4();
for(int i=1;i<=n;i++){
int x=a[i];
int lenl=i-l[i];
int lenr=r[i]-i;
sum1+=(lenl*lenr)*x;
}
cout<<sum-sum1<<nline;
}
signed main() {
ios::sync_with_stdio(false); cin.tie(nullptr);
// cin >> _; for (Case = 1; Case <= _; Case++)
solve(Case);
return 0;
}
T2:
待补。。。
T3:

思路:
预处理从根节点到每个点的异或和,然后两者异或值再跟lca的权值异或就是结果
代码:
tarjan求lca
#include <bits/stdc++.h>
#define int long long
int _ = 0, Case = 1;
using namespace std;
#define all(v) begin(v),end(v)
#define nline '\n'
int n, m;
const int N = 200010;
vector<int> h[N];
using PII = pair<int, int> ;
vector<PII> g[N];
int res[N], s[N], a[N];
int p[N];
int find(int x) {
return x != p[x] ? p[x] = find(p[x]) : p[x];
}
int vis[N];
void merge(int a, int b) {
int pa = find(a), pb = find(b);
if (pa != pb) {
p[pa] = pb;
}
}
void dfs(int u, int fa) {
for (auto i : h[u]) {
if (i == fa) continue;
s[i] ^= s[u];
dfs(i, u);
}
}
void tarjan(int u) {
vis[u] = 1;
for (auto i : h[u]) {
if (!vis[i]) {
tarjan(i);
merge(i, u);
}
}
for (auto [i, id] : g[u]) {
if (vis[i] == 2) {
int lca = find(i);
int t = s[u] ^ s[i] ^ a[lca];
res[id] = t;
}
}
vis[u] = 2;
}
void solve(int Case) {
cin >> n >> m;
for (int i = 1; i <= n; i++) cin >> a[i], s[i] = a[i];
for (int i = 1; i < n; i++) {
int a, b;
cin >> a >> b;
h[a].push_back(b);
}
for (int i = 1; i <= m; i++) {
int a, b;
cin >> a >> b;
g[a].push_back({b, i});
g[b].push_back({a, i});
}
for (int i = 1; i <= n; i++) p[i] = i;
dfs(1, -1);
tarjan(1);
for (int i = 1; i <= m; i++) {
cout << res[i] << nline;
}
}
signed main() {
ios::sync_with_stdio(false); cin.tie(nullptr);
// cin >> _; for (Case = 1; Case <= _; Case++)
solve(Case);
return 0;
}
T4:

思路:
可以求前缀和,与n取模之后最多n种可能,0直接输出,如果没有0,根据抽屉原理必然至少有两个数字重复
代码:
#include <bits/stdc++.h>
#define int long long
int _= 0, Case = 1;
using namespace std;
#define all(v) begin(v),end(v)
#define nline '\n'
const int N=500010;
int s[N];
int vis[N];
void solve(int Case) {
int n;
cin>>n;
for(int i=1;i<=n;i++){
cin>>s[i];
s[i]+=s[i-1];
s[i]%=n;
}
for(int i=1;i<=n;i++){
if(!s[i]){
cout<<i<<nline;
for(int j=1;j<=i;j++){
cout<<j<<' ';
}
return;
}
if(vis[s[i]]){
int l=vis[s[i]]+1;
cout<<i-l+1<<nline;
for(int j=l;j<=i;j++){
cout<<j<<' ';
}
return;
}
vis[s[i]]=i;
}
}
signed main() {
ios::sync_with_stdio(false); cin.tie(nullptr);
// cin >> _; for (Case = 1; Case <= _; Case++)
solve(Case);
return 0;
}
T5

思路:
m次操作,后面的操作会覆盖前面的操作,分为两类,操作2,最后会把所有的元素跟最大的y取max,操作1,需要跟x和后缀max(y)取最大值
代码:
#include <bits/stdc++.h>
#define int long long
int _ = 0, Case = 1;
using namespace std;
#define all(v) begin(v),end(v)
#define nline '\n'
const int N = 5000100;
struct T {
int op;
int x, y;
} q[N];
int mmax[N];
int a[N];
void solve(int Case) {
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; i++) cin >> a[i];
for (int i = 1; i <= m; i++) {
auto&[op, x, y] = q[i];
cin >> op;
if (op == 1) cin >> x >> y;
else cin >> y;
}
int s = 0;
for (int i = m; i >= 1; i--) {
auto[op, x, y] = q[i];
int t = 0;
if (op == 2) t = y;
mmax[i] = max(mmax[i + 1], t);
s = max(mmax[i], s);
}
for (int i = 1; i <= n; i++) a[i] = max(a[i], s);
for (int i = 1; i <= m; i++) {
auto[op, x, y] = q[i];
if (op == 1) {
a[x] = max(mmax[i], y);
}
}
for (int i = 1; i <= n; i++) cout << a[i] << ' ';
cout << nline;
}
signed main() {
ios::sync_with_stdio(false); cin.tie(nullptr);
// cin >> _; for (Case = 1; Case <= _; Case++)
solve(Case);
return 0;
}
xor inverse
数字大小只跟第一个不同的位置有关,可以统计出每个第一个不同位置的逆序对,然后贪心比较
代码:
const int N = 5000100;
int ch[N ][2];
int s[N ];
int f[N][2], idx;
void insert(int x) {
int p = 0;
for (int i = 31; i >= 0; i--) {
int t = 0;
if (x >> i & 1) t = 1;
if (!ch[p][t]) ch[p][t] = ++idx;
f[i][t]+=s[ch[p][t^1]];
p = ch[p][t];
s[p]++;
}
}
void solve(int Case) {
int n;
cin >> n;
int x;
for (int i = 1; i <= n; i++) cin >> x, insert(x);
int res = 0;
int sum = 0;
for (int i = 0; i <= 31; i++) {
if (f[i][1] < f[i][0]) res += 1 << i;
sum += min(f[i][1], f[i][0]);
}
cout << sum << ' ' << res << nline;
}
Closest Equals

思路:
最近的两个数肯定是相邻两个相同的数,进行离线操作,用线段树维护相邻的左端点和长度,每次查询取最小即可
代码:
#define nline '\n'
const int N = 500010, inf = 1e18;
int ans[N];
int a[N];
struct T {
int l, r, val;
} tr[N << 2];
struct TT {
int l, r, id;
bool operator<(const TT &t) const {
return r < t.r;
}
};
void build(int p, int l, int r) {
if (l == r) {
tr[p] = {l, r, inf};
return;
}
tr[p] = {l, r, inf};
int mid = l + r >> 1;
build(p << 1, l, mid);
build(p << 1 | 1, mid + 1, r);
}
void push_up(int p) {
tr[p].val = min(tr[p << 1].val, tr[p << 1 | 1].val);
}
int query(int p, int l, int r) {
if (tr[p].l >= l and tr[p].r <= r) return tr[p].val;
int mid = tr[p].l + tr[p].r >> 1;
if (r <= mid) return query(p << 1, l, r);
else if (l > mid) return query(p << 1 | 1, l, r);
return min(query(p << 1, l, r), query(p << 1 | 1, l, r));
}
void modify(int p, int x, int v) {
if (tr[p].l == x and tr[p].r == x) {
tr[p].val = v;
return;
}
int mid = tr[p].l + tr[p].r >> 1;
if (x <= mid) modify(p << 1, x, v);
else modify(p << 1 | 1, x, v);
push_up(p);
}
void solve(int Case) {
int n, m;
cin >> n >> m;
vector<TT>v, Q;
map<int, int> lst;
for (int i = 1; i <= n; i++) {
cin >> a[i];
}
for (int i = 1; i <= m; i++) {
int l, r;
cin >> l >> r;
Q.push_back({l, r, i});
}
sort(all(v));
sort(all(Q));
build(1, 1, n);
int idx = 1;
for (auto[l, r, id] : Q) {
for (int i = idx; i <= r; i++) {
if (lst[a[i]]) {
modify(1, lst[a[i]], i - lst[a[i]]);
}
lst[a[i]] = i;
}
idx = r + 1;
ans[id] = query(1, l, r);
}
for (int i = 1; i <= m; i++) {
if (ans[i] == inf) ans[i] = -1;
cout << ans[i] << nline;
}
}
503. 工作安排

每个工作只会消耗一个时间单位,按照截止时间排序,使用小根堆维护最小利益,每次跟最小利益比较
代码:
void solve(int Case) {
int n;
cin >> n;
using PII = pair<int, int> ;
vector<PII> v(n);
for (auto &[x, y] : v) {
cin >> x >> y;
}
sort(all(v));
int res = 0;
priority_queue<int,vector<int>,greater<int>> q;
for (auto [x, y] : v) {
if (q.size() < x) {
q.push(y);
res += y;
} else {
if(q.empty()) continue;
auto p=q.top();
if(p<y){
q.pop();
q.push(y);
res-=p;
res+=y;
}
}
}
cout << res << nline;
}
连续子序列

直接dp,f[x]存储以x结尾的最长连续子序列
代码:
const int N=200010;
int a[N];
map<int,int> f;
void solve(int Case) {
int n;
cin>>n;
for(int i=1;i<=n;i++){
int x;
cin>>x;
f[x]=max(f[x],1LL);
f[x]=max(f[x],f[x-1]+1);
}
int res=0;
int t=0;
for(auto [x,y]:f){
if(res<y) {
res=y;
t=x;
}
}
cout<<res<<nline;
for(int i=t-res+1;i<=t;i++){
cout<<i<<' ';
}
}
整齐的数组2

每次减去一个k,最后使得数字至少有一半相同,那么可以看作,起初有一半数字相同,然后给这些数加上k的某个倍数,最后变成给定的a数组,所以采用还原操作,给每个数减去一个数,然后求他们的约数中个数大于等于n/2的(注意0特判),就是结果;
代码:
const int N = 200010;
int a[N];
vector<int> get(int n) {
vector<int>a;
for (int i = 1; i <= n / i; i++) {
if (n % i == 0) {
a.push_back(i);
if (n / i != i) a.push_back(n / i);
}
}
return a;
}
void solve(int Case) {
int n;
cin >> n;
map<int, int> mp;
for (int i = 1; i <= n; i++) {
cin >> a[i];
}
sort(a + 1, a + 1 + n);
if (a[1] == a[n / 2]) {
cout << -1 << nline;
return;
}
int res = 0;
for (int i = 1; i <= n / 2 + 1; i++) {
map<int, int> mp;
int x = a[i];
for (int j = i; j <= n; j++) {
a[j] -= x;
}
int cnt = 0;
for (int j = i; j <= n; j++) {
auto c = get(a[j]);
if (!a[j]) cnt++;
for (auto v : c) {
mp[v]++;
}
}
for (int j = i; j <= n; j++) {
a[j] += x;
}
for (auto[x, y] : mp) {
if (y + cnt >= n / 2 ) {
res = max(res, x);
}
}
if (cnt >= n / 2) {
cout << -1 << nline;
return;
}
}
cout << res << nline;
}
三进制循环

树形dp,考虑每个根节点,他的左边和右边,结果应该是最长的左边和右边+1,根节点特殊处理即可
代码:
const int N = 500010;
vector<int> h[N];
int f[N][3][3];
int ans;
int d[N];
void dfs(int u, int fa) {
int t = d[u];
int a = 0, b = 0;
int x = (t + 1) % 3, y = (t + 2) % 3;
for (auto i : h[u]) {
if (i == fa) continue;
dfs(i, u);
a = max(a, f[i][x][y]);
b = max(b, f[i][y][x]);
}
for (int i = 0; i < 3; i++) {
if (i != t) f[u][t][i] = 1;
}
f[u][t][x] += a;
f[u][t][y] += b;
ans = max(ans, a + b + 1);
}
void solve(int Case) {
int n;
cin >> n;
for (int i = 1; i < n; i++) {
int a, b;
cin >> a >> b;
h[a].push_back(b);
h[b].push_back(a);
}
for (int i = 1; i <= n; i++) {
cin >> d[i];
}
dfs(1, -1);
cout << ans << nline;
}
树上逆序对

可以将题目转化位,每个根节点的子节点(l~r)小于根节点权值的个数,也就相当于求l到r小于x的数的个数,离线使用树状数组或线段树可求解
代码:
#define lowbit(x) x&(-x)
using PII = pair<int, int> ;
const int N = 500010;
int c[N];
struct T {
int x, l, r, len;
bool operator<(const T &t) const {
return x < t.x;
}
};
int ans[N];
int ask(int x) {
int res = 0;
for (; x; x -= lowbit(x)) res += c[x];
return res;
}
void add(int x, int y) {
for (; x < N; x += lowbit(x)) c[x] += y;
}
PII a[N];
void solve(int Case) {
int n;
cin >> n;
for (int i = 1; i <= n; i++) {
auto&[x, y] = a[i];
cin >> x;
y = i;
}
int idx = 1;
vector<T> v;
for (int k = 1; k < n; k++) {
for (int i = 1; (i - 1)*k + 2 <= n; i++) {
int l = (i - 1) * k + 2, r = i * k + 1;
int x = a[i].first;
v.push_back({x, l, r, k});
}
}
sort(all(v));
sort(a + 1, a + 1 + n);
for (auto [x, l, r, len] : v) {
while (idx <= n and a[idx].first < x) {
add(a[idx].second, 1);
idx++;
}
ans[len] += (ask(r) - ask(l - 1));
}
for (int i = 1; i < n; i++) cout << ans[i] << ' ';
}
字典序最小

思路:
使用栈来维护,如果栈内元素出现次数只有这一次,那就不能删掉,同时使用一个数字判重,避免重复假如栈中
代码:
const int N = 2000010;
int a[N];
int cnt[N];
int vis[N];
void solve(int Case) {
int n, k;
cin >> n >> k;
stack<int>stk;
vector<int> v;
for (int i = 1; i <= n; i++) cin >> a[i], cnt[a[i]]++;
for (int i = 1; i <= n; i++) {
if (!vis[a[i]]) {
while (stk.size() and a[i]<stk.top() and cnt[stk.top()]>0) {
vis[stk.top()]=false;
stk.pop();
}
stk.push(a[i]);
vis[a[i]]=true;
}
cnt[a[i]]--;
}
while(stk.size()){
v.push_back(stk.top());
stk.pop();
}
reverse(all(v));
for(int i=0;i<k;i++){
cout<<v[i]<<((i==k-1)? '\n':' ');
}
}
611. 拆拆

思路:
对于每个x进行质因数分解,假如每个质因子有x个,相当于把x个数放到y个不同的盒子里,可以空,就是组合数C(y+x-1,y-1);还有偶数个负号2^(n-1)
代码:
#pragma GCC optimize(1)
#pragma GCC optimize(2)
#pragma GCC optimize(3,"Ofast","inline")
#include <bits/stdc++.h>
#define int long long
int _ = 0, Case = 1;
using namespace std;
#define all(v) begin(v),end(v)
#define nline '\n'
const int N = 1000500, mod = 1e9 + 7;
int fact[N], infact[N], m[N];
int vis[N];
int a[N];
int cnt = 0;
int prime[N + 3], pcnt;
bool siv[N + 3];
int work(int TARGET) {
for (int i = 2; i < N; i++) {
if (!siv[i]) {
prime[++pcnt] = i;
m[i] = i;
}
for (int j = 1; j <= pcnt && i * prime[j] < N; j++) {
siv[i * prime[j]] = true;
m[prime[j] * i] = prime[j];
if (i % prime[j] == 0) {
break;
}
}
}
return -1;
}
int q_p(int a, int b, int p) {
int res = 1 % p;
while (b) {
if (b & 1) res = res * a % p;
b >>= 1;
a = a * a % p;
}
return res;
}
void init() {
fact[0] = infact[0] = 1;
for (int i = 1; i < N; i++) {
fact[i] = fact[i - 1] * i % mod;
infact[i] = q_p(fact[i], mod - 2, mod);
}
}
int C(int a, int b) {
return fact[a] * infact[a - b] % mod * infact[b] % mod;
}
void solve(int Case) {
int x, y;
scanf("%lld%lld", &x, &y);
int res = 1;
while (x > 1) {
int t = x % 2 == 0 ? 2 : m[x];
int cnt = 0;
while (x % t == 0) x /= t, cnt++;
res*=C(cnt+y-1,y-1);
res%=mod;
}
res %= mod;
res *= q_p(2, y - 1, mod);
res %= mod;
printf("%lld\n", res);
}
signed main() {
init();
work(N);
//cout<<pcnt<<nline;
scanf("%lld", &_); for (Case = 1; Case <= _; Case++)
solve(Case);
return 0;
}
tips:
埃式筛的同时也可以对每个数质因数分解,复杂度大概nlogn
线性筛之后再对一个数字质因数分解,复杂度大概是logn
work(N);//筛
while (x > 1) {
int t = x % 2 == 0 ? 2 : m[x];
int cnt = 0;
while (x % t == 0) x /= t, cnt++;
}
最大公约数

思路:
每一段之和的最大公约数一定是总和的最大公约数,枚举总和的约数,计算最大公约数是x时能k段,则1~k-1也能够被x分解出来
代码:
#include <bits/stdc++.h>
#define int long long
int _ = 0, Case = 1;
using namespace std;
#define all(v) begin(v),end(v)
#define nline '\n'
const int N = 200010;
int n;
int s[N];
int ans[N];
void cal(int x) {
int res = 0;
map<int,int> mp;
for (int i = 1; i <= n; i++) {
mp[s[i]%x]++;
}
for(auto [x,y]:mp){
res=max(res,y);
}
ans[res] = max(ans[res], x);
}
void solve(int Case) {
cin>>n;
for (int i = 1; i <= n; i++) {
cin >> s[i];
s[i] += s[i - 1];
}
int t = s[n];
for (int i = 1; i <= sqrt(t); i++) {
if (t % i == 0) {
cal(i);
cal(t/i);
}
}
for(int i=n;i>=0;i--){
ans[i]=max(ans[i+1],ans[i]);
}
for(int i=1;i<=n;i++) cout<<ans[i]<<nline;
}
signed main() {
ios::sync_with_stdio(false); cin.tie(nullptr);
// cin >> _; for (Case = 1; Case <= _; Case++)
solve(Case);
return 0;
}
括号序列

思路
动态规划,f[i]表示以i结尾的连续子段括号的数量p[i]表示与之匹配的左括号位置,
f[i]=f[p[i]-1]+1
代码:
const int N = 1000010;
char s[N];
int p[N], f[N];
void solve() {
scanf("%s", s + 1);
stack<int> stk;
int n = strlen(s + 1);
int ans = 0;
int cnt = 0;
for (int i = 1;i <= n;i++) {
if (s[i] == '(') {
stk.push(i);
}
else {
if (stk.size()) p[i] = stk.top(), stk.pop();
}
}
for (int i = 1;i <= n;i++) {
if (p[i]) {
f[i] = f[p[i] - 1] + 1;
printf("s %lld %lld\n",i,f[i]);
ans += f[i];
}
}
printf("%lld\n", ans);
}
合适数对

题意:
找到有多少对数字(p,q)满足\(p*q=a_{1}^{t1*k}*a_{2}^{t2*k}*a_{3}^{t3*k}*.....\)
对每个数字进行质因数分解,然后寻找满组当前p的q的个数,质因数分解可以在logn复杂度完成
代码:
using namespace std;
const int N = 1000010, M = 10000010;
int prime[M], vis[M], pcnt;
int cnt[M];
int a[N];
int m[M];
void sieve(int n) {
vis[1] = true;
vis[0] = true;
for (int i = 2; i < n; i++) {
if (!vis[i]) prime[++pcnt] = i, m[i] = i;
for (int j = 1; prime[j] * i < n; j++) {
m[prime[j] * i] = prime[j];
vis[prime[j] * i] = true;
if (i % prime[j] == 0) break;
}
}
}
int qmi(int a, int b) {
int res = 1;
while (b) {
if (b & 1) res = res * a;
a = a * a;
b >>= 1;
}
return res;
}
void solve() {
int n, k;
n=read(),k=read();
for (int i = 1; i <= n; i++) a[i]=read();
int ans = 0;
for (int i = 1; i <= n; i++) {
int x = a[i];
int p = 1;
int q = 1;
while (x > 1) {
int t = x % 2 == 0 ? 2 : m[x];
int cnt = 0;
while (x % t == 0) x /= t, cnt++;
cnt %= k;
p *= qmi(t, cnt);
cnt = (k - cnt) % k;
q *= qmi(t, cnt);
}
if (q<0 or q>M) q = 0;
ans += cnt[q];
cnt[p]++;
}
printf("%lld",ans);
}
体育节
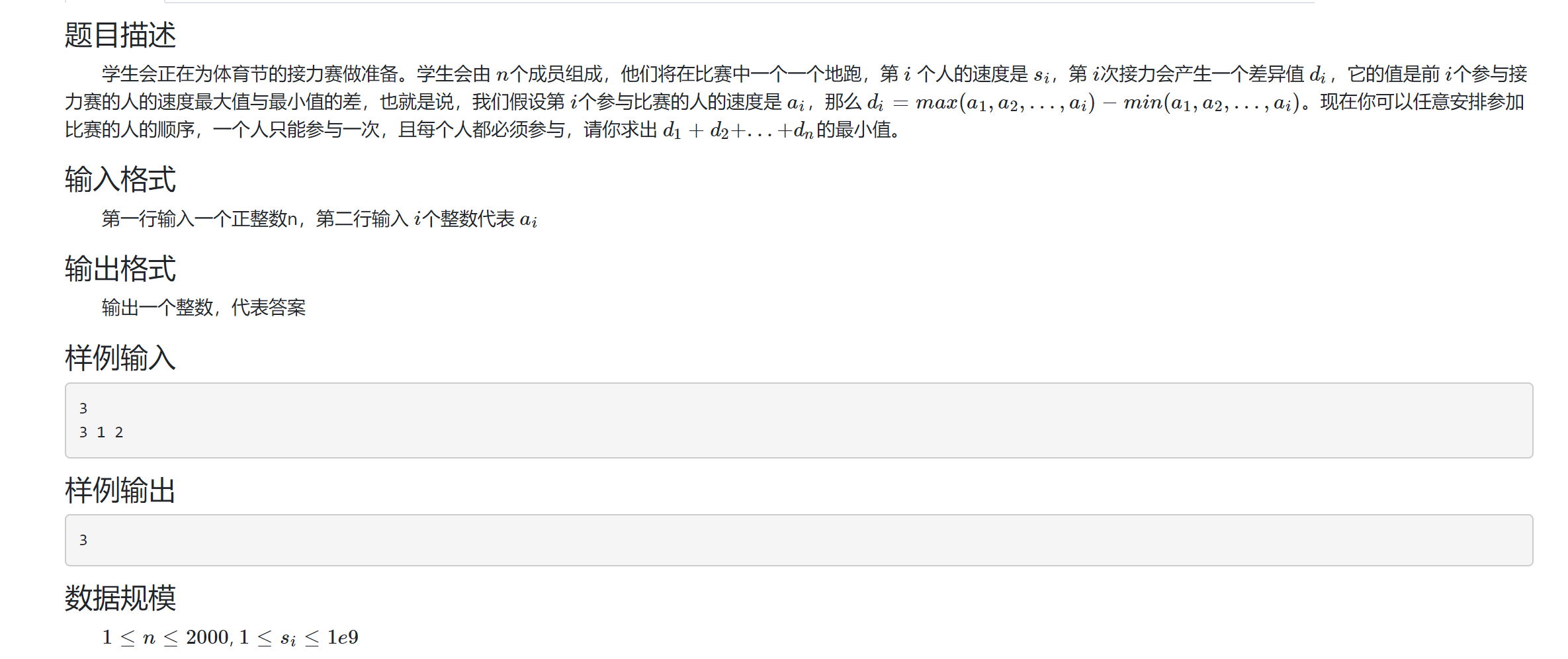
思路
每次优先选择相差较小的开始,相邻两个元素相差最小,所以先排序,
然后区间dp,f[l][r]=min(f[l+1][r],f[l][r-1])+a[r]-a[l]
代码:
const int N = 2020;
int a[N];
int f[N][N];
void solve() {
int n = read();
for (int i = 1;i <= n;i++) a[i] = read();
sort(a + 1, a + 1 + n);
for (int len = 1;len <= n;len++) {
for (int l = 1;l + len - 1 <= n;l++) {
int r = l + len - 1;
f[l][r] = min(f[l][r - 1] + a[r] - a[l], f[l + 1][r] + a[r] - a[l]);
}
}
printf("%lld\n", f[1][n]);
clean();
}
namonamo

思路:
二进制枚举a和b可以得到子序列,n的数据太大,可以采用折半搜索,前半段的可以搜出来多出来的后缀做后半段的前缀,如果刚好一样就说明可以
代码:
using namespace std;
char s[1010];
int n;
bool ok = false;
map<string, int>mp;
void dfs(int u, string a, string b) {
for (int i = 0;i < min(a.size(), b.size());i++) {
if (a[i] != b[i]) return;
}
if (u == n / 2 + 1) {
if (a.size() > b.size()) {
string prefix = a.substr(b.size());
mp[prefix]++;
}
else {
string prefix = b.substr(a.size());
mp[prefix]++;
}
return;
}
a.push_back(s[u]);
dfs(u + 1, a, b);
a.pop_back();
b.push_back(s[u]);
dfs(u + 1, a, b);
b.pop_back();
}
void dfs1(int u, string a, string b) {
if (ok) return;
if (u == n + 1) {
reverse(all(a));
reverse(all(b));
for (int i = 0;i < min(a.size(), b.size());i++) {
if (a[i] != b[i]) return;
}
if (a.size() > b.size()) {
string suffix = a.substr(b.size());
reverse(all(suffix));
if (mp[suffix] > 0) ok = true;
return;
}
else {
string suffix = b.substr(a.size());
reverse(all(suffix));
if (mp[suffix] > 0) ok = true;
return;
}
}
a.push_back(s[u]);
dfs1(u + 1, a, b);
a.pop_back();
b.push_back(s[u]);
dfs1(u + 1, a, b);
b.pop_back();
}
void solve() {
ok = false;
mp.clear();
scanf("%s", s + 1);
n = strlen(s + 1);
dfs(1, "", "");
dfs1(n / 2 + 1, "", "");
if (ok) puts("possible");
else puts("impossible");
}
折半搜索例题
世界冰球锦标赛
code
int a[N];
int n, m;
vector<int> v;
int ans = 0;
void dfs(int u, int sum) {
if (sum > m) return;
if (u == n / 2 + 1) {
if (sum <= m) v.push_back(sum);
return;
}
dfs(u + 1, sum);
dfs(u + 1, sum + a[u]);
}
void dfs1(int u, int sum) {
if (sum > m) return;
if (u == n + 1) {
int t = m - sum;
auto it = upper_bound(all(v), t);
int p = it - v.begin();
ans += p;
return;
}
dfs1(u + 1, sum);
dfs1(u + 1, sum + a[u]);
}
void solve() {
n = read();
m = read();
for (int i = 1;i <= n;i++) a[i] = read();
dfs(1, 0);
sort(all(v));
dfs1(n / 2 + 1, 0);
printf("%lld\n", ans);
clean();
}
数字替换
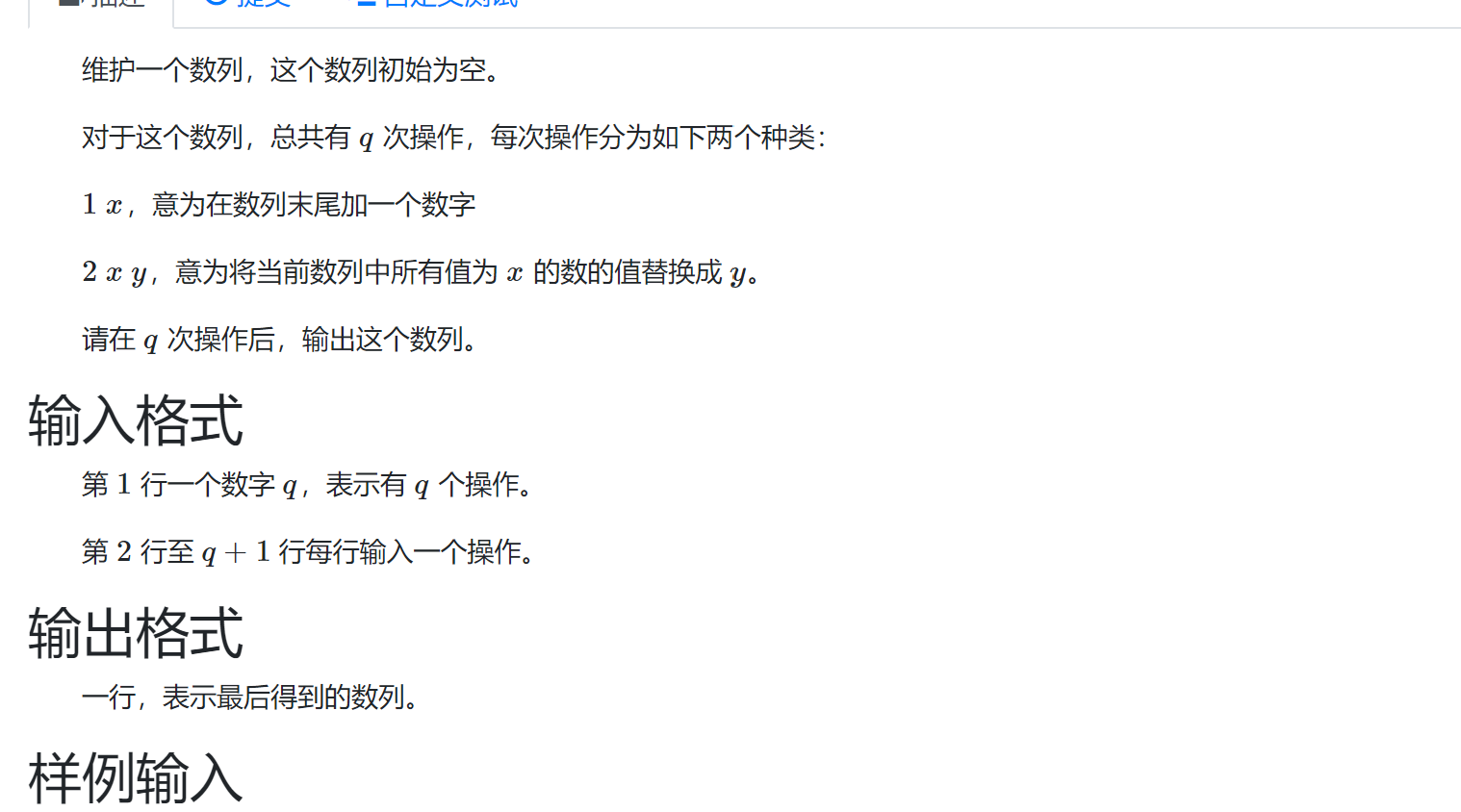
思路:
倒序维护,注意不能路径压缩,可能会导致前面一些数字发生变化
代码:
struct T {
int op, x, y;
}q[1000010];
int ans[1000010], p[1000100];
void solve() {
int m = read();
int n = 0;
for (int i = 1;i <= m;i++) {
int op = read(), x = read(), y = -1;
if (op == 2) {
y = read();
}
q[i] = { op,x,y };
}
for (int i = 1;i <= N - 5;i++) p[i] = i;
for (int i = m;i >= 1;i--) {
auto& [op, x, y] = q[i];
if (op == 2) {
p[x] = p[y];
}
else {
x = p[x];
}
}
for (int i = 1;i <= m;i++) {
auto [op, x, y] = q[i];
if (op == 1) {
ans[++n] = x;
}
}
for (int i = 1;i <= n;i++) {
printf("%lld ", ans[i]);
}
clean();
}
质区间长度
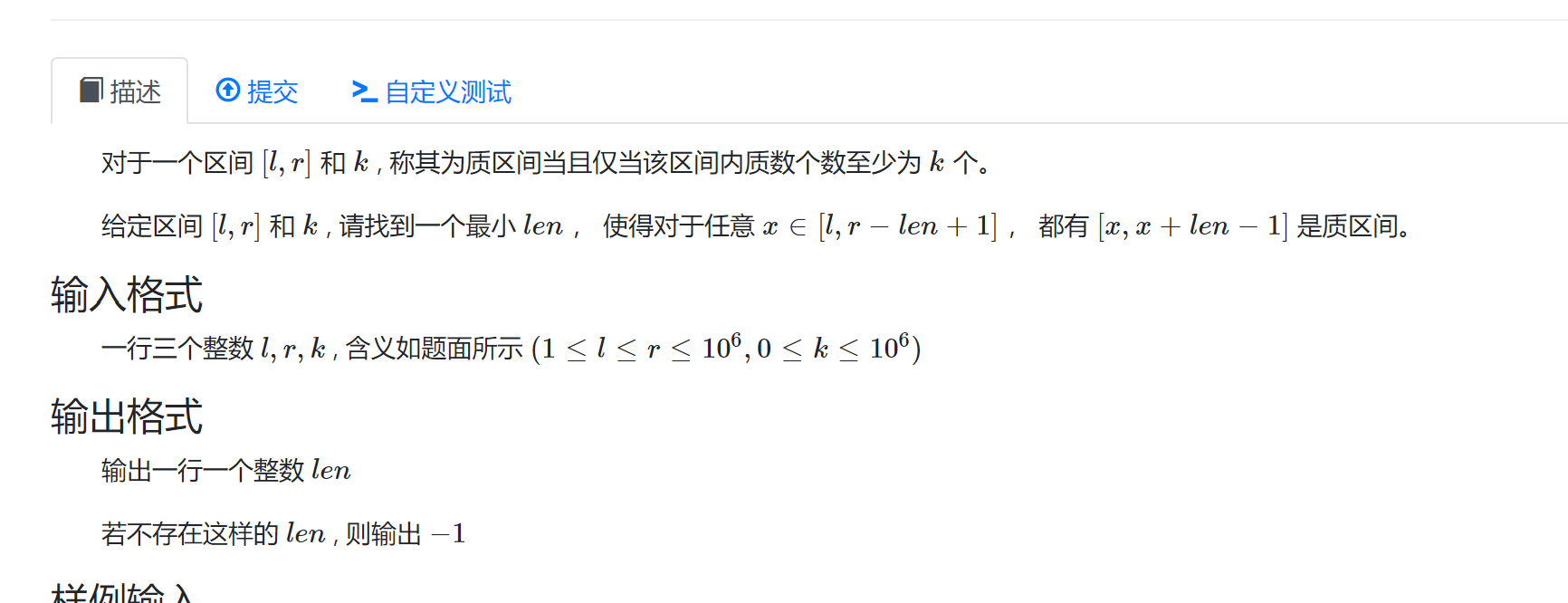
思路:
筛质数然后前缀和统计区间质数个数二分
代码:
int a[N], s[N];
int vis[N], prime[N], m[N], pcnt;
void sieve(int n) {
vis[1] = true;
vis[0] = true;
for (int i = 2; i < n; i++) {
if (!vis[i]) prime[++pcnt] = i, m[i] = i;
for (int j = 1; prime[j] * i < n; j++) {
m[prime[j] * i] = prime[j];
vis[prime[j] * i] = true;
if (i % prime[j] == 0) break;
}
}
}
int l, r, k;
bool check(int mid) {
for (int i = l;i + mid - 1 <= r;i++) {
if (s[i + mid - 1] - s[i - 1] < k) return false;
}
return true;
}
void solve() {
sieve(N - 5);
l = read(), r = read(), k = read();
if (!k) {
printf("%lld\n", 1LL);
return;
}
for (int i = l;i <= r;i++) {
if (!vis[i]) s[i] = 1;
s[i] += s[i - 1];
}
int ans = inf;
int a = 0, b = r - l ;
while (a < b) {
int mid = a + b >> 1;
if (check(mid)) b = mid;
else a = mid + 1;
}
if (b==r-l) b = -1;
printf("%lld\n", b);
clean();
}
矩形划分

思路:
欧拉公式:点数-边数-面数=2
点数是x2+y2+x*y+逆序对
每个点会产生3~4的贡献最后/2
代码:
int C[N];
#define lowbit(x) x&(-x)
void add(int x, int y) {
for (; x < N; x += lowbit(x)) C[x] += y;
}
int ask(int x) {
int res = 0;
for (; x; x -= lowbit(x)) res += C[x];
return res;
}
vector<int> c;
int find(int x) {
return lower_bound(all(c), x) - c.begin() + 1;
}
void solve(int Case) {
int n, m;
scanf("%lld%lld", &n, &m);
using PII = pair<int, int> ;
int x, y;
vector<PII> v;
scanf("%lld%lld", &x, &y);
for (int i = 0; i < x; i++) {
int a, b;
scanf("%lld%lld", &a, &b);
v.push_back({a, b});
c.push_back(b);
}
sort(all(v));
sort(all(c));
int ans = 0;
c.erase(unique(all(c)), c.end());
for (int i = x - 1; i >= 0; i--) {
int x = find(v[i].second);
ans += ask(x - 1);
add(x, 1);
}
v.clear();
c.clear();
for (int i = 0; i < y; i++) {
int a, b;
scanf("%lld%lld", &a, &b);
v.push_back({a, b});
c.push_back(b);
}
sort(all(v));
sort(all(c));
memset(C, 0, sizeof C);
c.erase(unique(all(c)), c.end());
for (int i = y - 1; i >= 0; i--) {
int x = find(v[i].second);
ans += ask(x - 1);
add(x, 1);
}
int a = (x + y) * 2;
int b = x * y + ans;
printf("%lld\n", (a + 2 * b) / 2 + 1);
}
Mouse Hunt

思路:
tarjan缩点之后变成DAG每个终点的SCC中最小的点就是贡献
代码:
const int N = 200010;
int p[N], w[N];
int c[N];
int dout[N];
vector<int> h[N], g[N];
int dfn[N], low[N], id[N];
int deg[N];
bool vis[N];
stack<int> s;
int S[N];
int idx, scc_cnt;
void tarjan(int u) {
dfn[u] = low[u] = ++idx;
vis[u] = true;
s.push(u);
for (auto i : h[u]) {
if (!dfn[i]) {
tarjan(i);
low[u] = min(low[u], low[i]);
} else if (vis[i]) low[u] = min(low[u], dfn[i]);
}
if (dfn[u] == low[u]) {
++scc_cnt;
int y;
do {
y = s.top();
s.pop();
id[y] = scc_cnt;
S[scc_cnt]++;
c[scc_cnt] = min(c[scc_cnt], w[y]);
vis[y] = false;
}
while (y != u);
}
}
void solve(int Case) {
int n = read();
memset(c, 0x3f, sizeof c);
for (int i = 1; i <= n; i++) {
w[i] = read();
}
for (int i = 1; i <= n; i++) {
p[i] = read();
h[i].push_back(p[i]);
}
for (int i = 1; i <= n; i++) {
if (!dfn[i]) {
tarjan(i);
}
}
for (int i = 1; i <= n; i++) {
for (auto j : h[i]) {
int a = id[i], b = id[j];
if (a != b) {
dout[a]++;
g[a].push_back(b);
}
}
}
int res = 0;
for (int i = 1; i <= scc_cnt; i++) {
if (!dout[i]) res += c[i];
}
printf("%lld\n", res);
}
第二大数字和
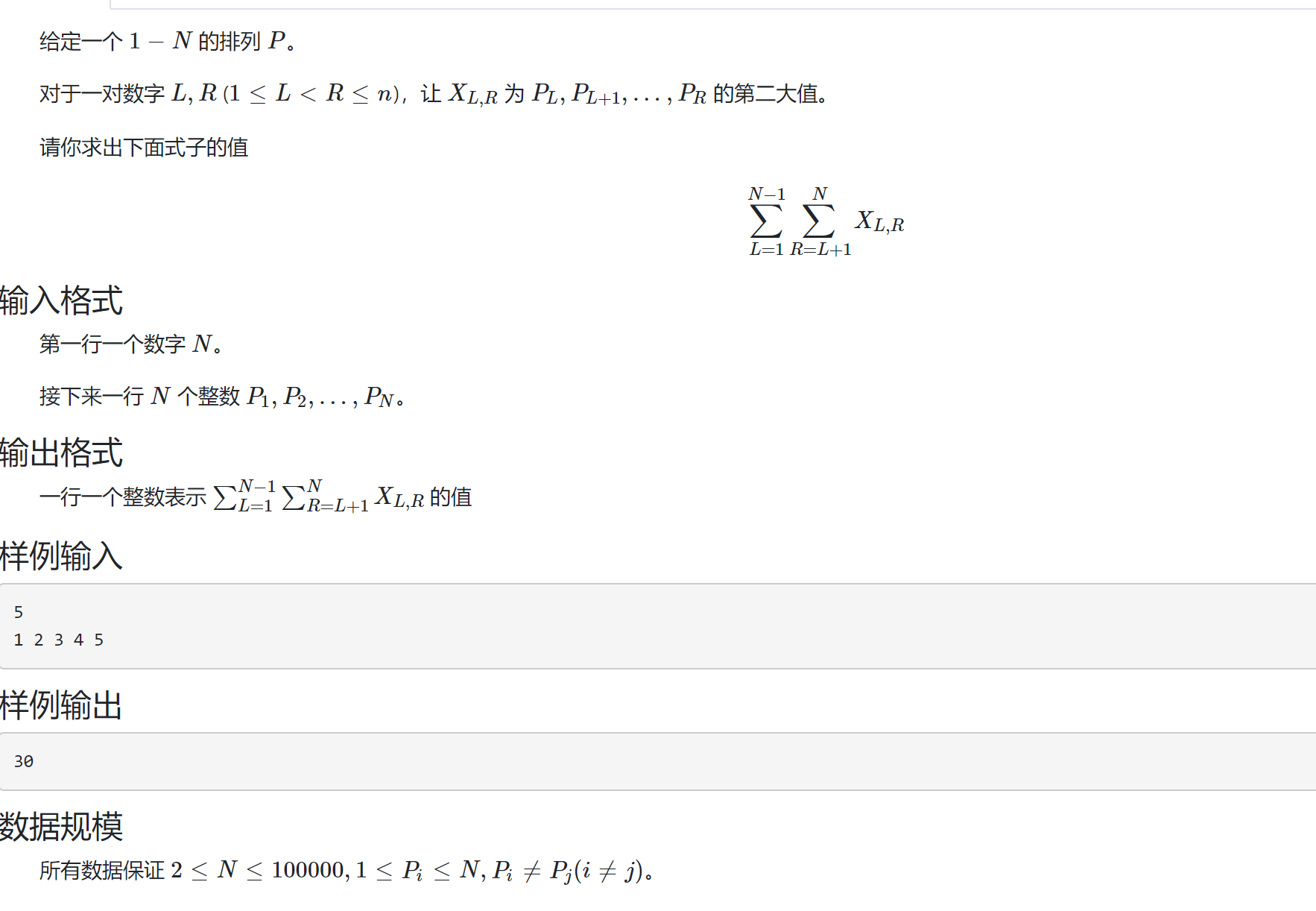
思路:
题目大概是求所有的大于2的区间中第二大的数的和,
直接没法做可以考虑每个数字的贡献,最大的数字肯定没有贡献;
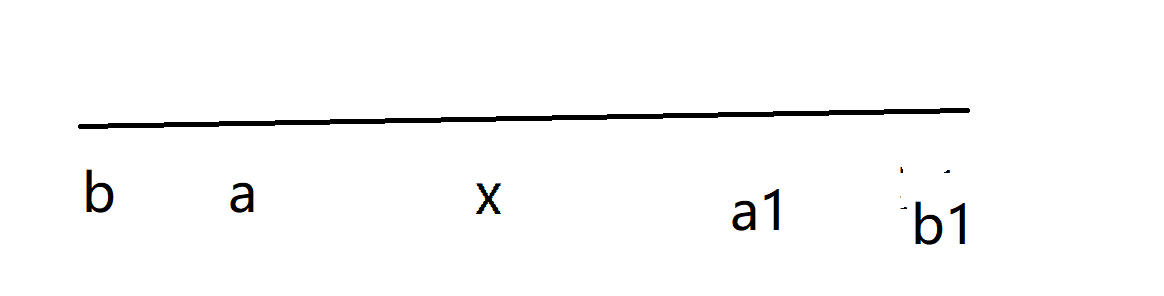
b>a>x
假如选择a到x,那么 b+1 到a-1 ,x到a1-1,这些与 a到x 相接贡献都是x,第一个数字可以使用单调栈,第二个大于的数字可以使用线段树二分寻找
#define read() FastIO::read()
#define clean() FastIO::flush()
const int N = 200010;
int a[N];
#define ls(x) x<<1
#define rs(x) x<<1 |1
struct tree {
int l, r;
int mmax;
};
struct Segment_Tree {
tree tr[N << 2];
int pos[N];
void pushup(tree &p, tree &l, tree &r) {
p.mmax = max(l.mmax, r.mmax);
}
void pushup(int p) {
pushup(tr[p], tr[ls(p)], tr[rs(p)]);
}
void build(int p, int l, int r) {
if (l == r) {
tr[p] = {l, r, a[l]};
pos[l] = p;
}
else {
tr[p] = {l, r};
int mid = l + r >> 1;
build(ls(p), l, mid);
build(rs(p), mid + 1, r);
pushup(p);
}
}
tree query(int p, int l, int r) {
if (tr[p].l >= l and tr[p].r <= r) return tr[p];
int mid = tr[p].l + tr[p].r >> 1;
if (r <= mid) return query(ls(p), l, r);
else if (l > mid) return query(rs(p), l, r);
else {
tree ret;
auto left = query(ls(p), l, r);
auto right = query(rs(p), l, r);
pushup(ret, left, right);
return ret;
}
}
};
Segment_Tree ST;
int findL(int l, int r, int x) {
if (l == r) return l;
int mid = l + r >> 1;
if (ST.query(1, mid + 1, r).mmax > x) return findL(mid + 1, r, x);
else if (ST.query(1, l, mid).mmax > x) return findL(l, mid, x);
}
int findR(int l, int r, int x) {
if (l == r) {
return l;
}
int mid = l + r >> 1;
if (ST.query(1, l, mid).mmax > x) return findR(l, mid, x);
else if (ST.query(1, mid + 1, r).mmax > x) return findR(mid + 1, r, x);
}
int l[N], r[N];
int n;
void cal() {
a[0] = 1e18;
stack<int> stk;
stk.push(0);
for (int i = 1; i <= n; i++) {
while (stk.size() and a[stk.top()] < a[i]) stk.pop();
l[i] = stk.top();
stk.push(i);
}
}
void cal1() {
a[n + 1] = 1e18;
stack<int> stk;
stk.push(n + 1);
for (int i = n; i >= 1; i--) {
while (stk.size() and a[stk.top()] < a[i]) stk.pop();
r[i] = stk.top();
stk.push(i);
}
}
void solve(int Case) {
n = read();
for (int i = 1; i <= n; i++) a[i] = read();
cal();
cal1();
ST.build(1, 0, n + 1);
int ans = 0;
for (int i = 1; i <= n; i++) {
int x = a[i];
if (x == n) continue;
if (l[i] != 0) {
ans += x;
int a = (r[i] - i - 1);
ans += (r[i] - i - 1) * x;
int L = l[l[i]];
int pl = findL(L, l[i] - 1, x);
int b = l[i] - pl - 1;
ans += a * b * x;
ans += (l[i] - pl - 1) * x;
}
if (r[i] != n + 1) {
ans += x;
ans += (i - l[i] - 1) * x;
int a = i - l[i] - 1;
int R = r[r[i]];
int pr = findR(r[i] + 1, R, x);
int b = pr - r[i] - 1;
ans += a * b * x;
ans += (pr - r[i] - 1) * x;
}
}
printf("%lld\n", ans);
}
最长上升子序列计数:
思路:
考虑朴素版本,f[i]表示子序列长度,d[i]表示最长的个数,f[i]=max(f[j]+1),同时更新d[i]
使用线段树优化,每次计算i结尾的最长上升子序列,是前i-1个数中小于a[i]的最大值更新过来,可以使用线段树维护,最大值和最大值的数量,更新的时候如果长度相同就累加,大于的话就更新
代码:
#include <bits/stdc++.h>
#define int long long
int _ = 0, Case = 1;
using namespace std;
#define all(v) begin(v),end(v)
#define nline '\n'
const int N = 400010, mod = 1e9 + 7;
#define lowbit(x) x&(-x)
#define ls(x) x<<1
#define rs(x) x<<1 |1
struct tree {
int l, r;
int sum, max;
};
struct Segment_Tree {
tree tr[N << 2];
int pos[N];
void pushup(tree &p, tree &l, tree &r) {
p.max = max(l.max, r.max);
if (l.max == r.max) {
p.sum = l.sum + r.sum;
p.sum %= mod;
} else if (l.max > r.max) {
p.sum = l.sum;
} else p.sum = r.sum;
p.sum %= mod;
}
void pushup(int p) {
pushup(tr[p], tr[ls(p)], tr[rs(p)]);
}
void build(int p, int l, int r) {
if (l == r) {
tr[p] = {l, r, 0, 0};
pos[l] = p;
}
else {
tr[p] = {l, r};
int mid = l + r >> 1;
build(ls(p), l, mid);
build(rs(p), mid + 1, r);
pushup(p);
}
}
void modify1(int p, int x, int y, int len) {
p = pos[x];
if (tr[p].max < y) tr[p].max = y, tr[p].sum = len;
else if (tr[p].max == y) tr[p].sum += len;
tr[p].sum %= mod;
for (; p >>= 1;) pushup(p);
}
tree query(int p, int l, int r) {
if (tr[p].l >= l and tr[p].r <= r) return tr[p];
int mid = tr[p].l + tr[p].r >> 1;
if (r <= mid) return query(ls(p), l, r);
else if (l > mid) return query(rs(p), l, r);
else {
tree ret;
auto left = query(ls(p), l, r);
auto right = query(rs(p), l, r);
pushup(ret, left, right);
return ret;
}
}
};
Segment_Tree ST;
vector<int> v;
int a[N], f[N], d[N];
int find(int x) {
return lower_bound(all(v), x) - v.begin() + 1;
}
void solve(int Case) {
int n;
scanf("%lld", &n);
for (int i = 1; i <= n; i++) scanf("%lld", &a[i]), v.push_back(a[i]);
sort(all(v));
v.erase(unique(all(v)), v.end());
int res = 0;
ST.build(1, 1, n);
for (int i = 1; i <= n; i++) {
int x = find(a[i]);
int t = 0;
if (x != 1) {
t = ST.query(1, 1, x - 1).max;
}
f[i] = t + 1;
if (x != 1)
d[i] = ST.query(1, 1, x - 1).sum;
else d[i] = 1;
if (!d[i]) d[i] = 1;
ST.modify1(1, x, f[i], d[i]);
res = max(res, f[i]);
}
int ans = 0;
for (int i = 1; i <= n; i++) {
if (f[i] == res) ans += d[i], ans %= mod;
}
printf("%lld\n", ans);
}
signed main() {
// for (scanf("%lld", &_), Case = 1; Case <= _; Case++)
solve(Case);
return 0;
}


