关于卡诺图的一点想法

卡诺图是逻辑表达式的一种表示方法 ，即将逻辑上的相邻转换为几何上的相邻，这种转换是如何做到的是这篇博客要写的内容。

 

逻辑上的相邻指两个逻辑表达式之间只有一个变量的状态不同。

几何上的相邻表示图上的两个矩形至少有一条边共享（包括对边界共享）。

这里讨论的变量a，b，c，...均为二值逻辑变量，即只有两种状态a、a'，b、b'，c、c'，...

 

1、对于一个变量a，它能构成的最小项表达式只有两种：a和a'，需要用到两个矩形，由于每个表达式只有一个逻辑相邻的表达式，每个矩形只有一条边共享出去，那么用图形来表示它们相邻很简单，如下图所示：

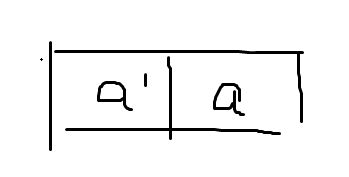
这是一变量的卡诺图。

2、对于两个变量a和b，它们能构成的最小项有4种ab、ab'、a'b、a'b'，需要用到4个矩形，由于每个表达式有两个逻辑相邻的表达式，每个矩形一定会有两条边共享出去，要使它们在图形上两两相邻可以这样做：

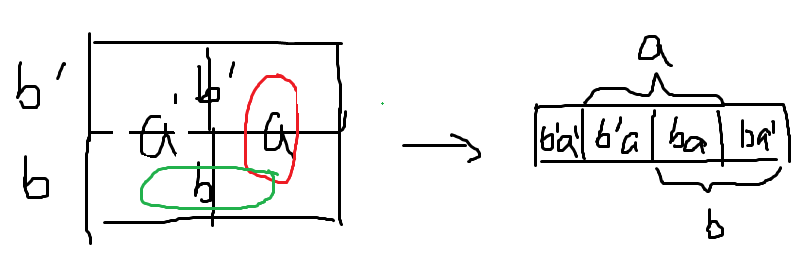
由于对边界也是共享的，可以将这四个正方形矩形展开成一条直线，变成右边这种形式。这是两变量的卡诺图。

3、对于三个变量a、b、c，它们能构成的最小项有8种，要使它们在图形上两两相邻需要8个矩形，每个矩形一定会有三条边共享出去：

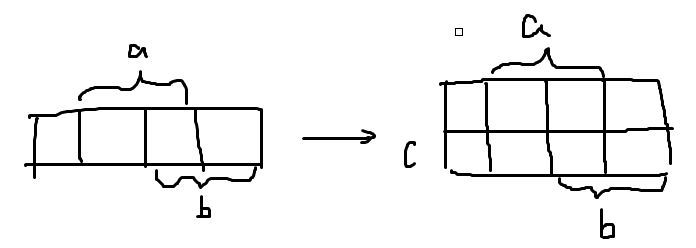
由二变量的卡诺图可知行数一定时列上的表达式一定是相邻的，又由纵向只有c和c'两种状态，一定相邻，所以这样得来的八个矩形中的表达式也一定是逻辑相邻的，这是三变量的卡诺图。

4、对于四个变量a、b、c、d，它们能构成的最小项有16种，需要用到16个矩形，每个矩形会有四条边共享出去，自然而然可以用得到二变量卡诺图的方法将三变量卡诺图向下折叠，得到下面的四变量卡诺图：

5、对于五和六变量变量的卡诺图，很明显矩形的四条边已经不够用了，需要向空间延申，共享一个面和两个面，得到相应的卡诺图：

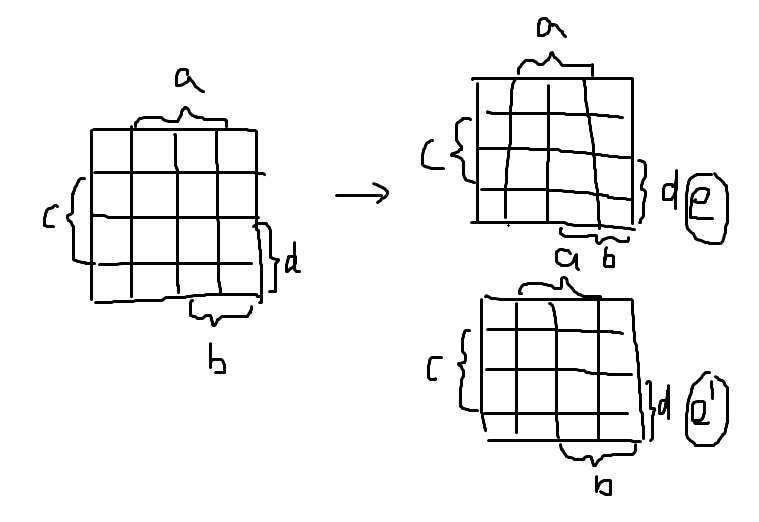
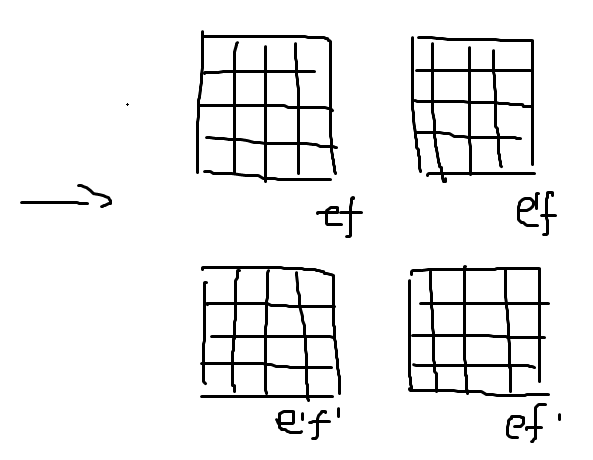
6、七变量、八变量甚至更多变量的估计就要多维卡诺图来表示，虽然可以折叠起来画在一张图上，但是对于化简逻辑表达式肯定是增加难度了，不予理会。

 

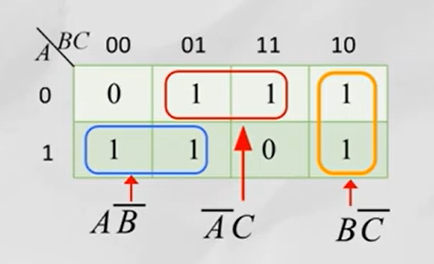
将待化简的逻辑表达式的各项填入相应的位置并且找相邻项合并就是我们用的卡诺图化简法了。

 

有意思的是，卡诺图的定义和我们刚学的格雷码很像，它们的相邻两项都是逻辑相邻的。如果我们从二阶的卡诺图开始不向下展开而是继续不断向右展开，就可以得到如下的图形和最小项表达式：

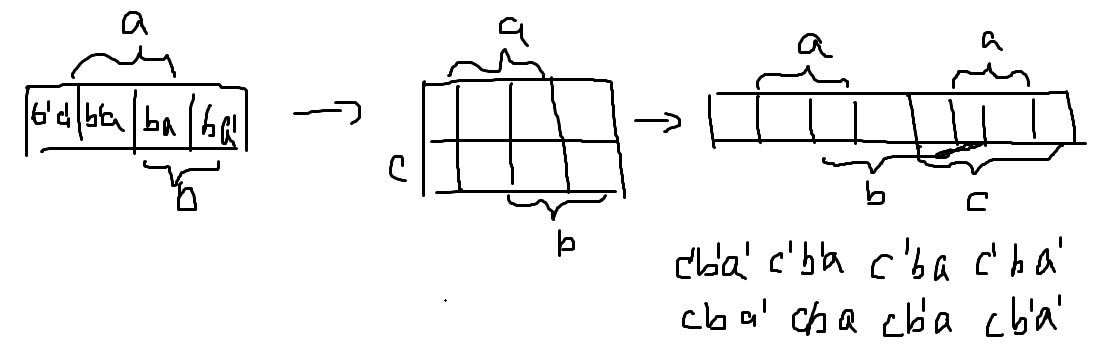
 很明显，将a、b、c=1和a'，b'，c'=0代入上式得到的就是三位的格雷码，更高位的格雷码也是一样的构造方法。