egret-贝塞尔曲线实现游戏里物体的曲线移动

egret-贝塞尔曲线实现游戏里物体的曲线移动

1.Bezier曲线的原理

Bezier曲线是应用于二维图形的曲线。曲线由顶点和控制点组成，通过改变控制点坐标可以改变曲线的形状。

 

 

 

 

 

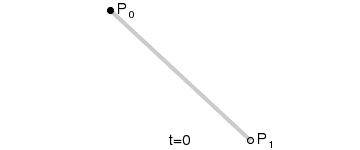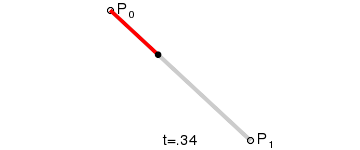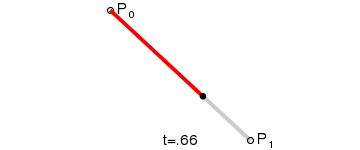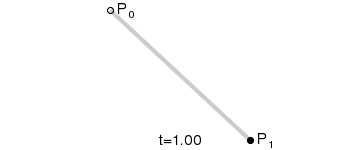
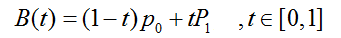
 一次Bezier曲线是由P0至P1的连续点，描述的一条线段

二次Bezier曲线公式

 

 

 

 

 

 

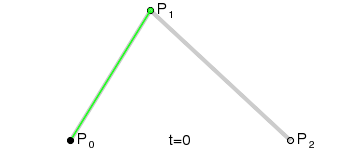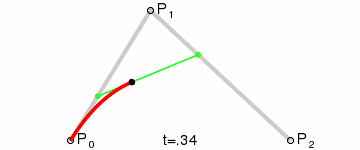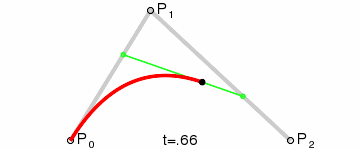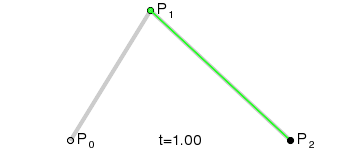
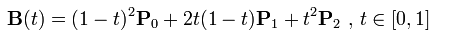
二次Bezier曲线是 P0至P1 的连续点Q0和P1至P2 的连续点Q1 组成的线段上的连续点B(t)，描述一条抛物线。

 三次Bezier曲线公式：

 

 

 

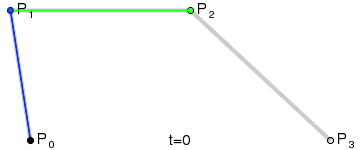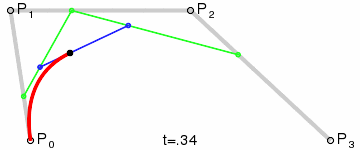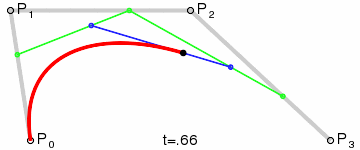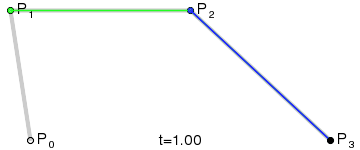
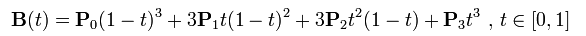
 Bezier曲线二次跟三次的实现，其实就是根据几个连续点，还有给定的t，绘制出点。

class BezierUtil {
    /**
     * 根据传入的锚点组返回贝塞尔曲线上的一组点,返回类型为egret.Point[];
     * @param pointsData 锚点组,保存着所有控制点的x和y坐标,格式为[x0,y0,x1,y1,x2,y2...]
     * @param pointsAmount 要获取的点的总个数，实际返回点数不一定等于该属性，与范围有关
     * @returns egret.Point[];
     */
    public static createBezierPoints(pointsData: number[], pointsAmount: number): egret.Point[] {
        let points = [];
        for (let i = 0; i < pointsAmount; i++) {
            const point = this.getBezierPointByFactor(pointsData, i / pointsAmount);
            if (point)
                points.push(point);
        }
        return points;
    }
    /**
     * 根据锚点组与取值系数获取贝塞尔曲线上的一点
     * @param pointsData 锚点组,保存着所有控制点的x和y坐标,格式为[x0,y0,x1,y1,x2,y2...]
     * @param t 取值系数
     * @returns egret.Point
     */
    public static getBezierPointByFactor(pointsData: number[], t: number): egret.Point {
        let i = 0;
        let x = 0, y = 0;
        const len = pointsData.length;
        //根据传入的数据数量判断是二次贝塞尔还是三次贝塞尔
        if (len / 2 == 3) {
            //二次
            const x0 = pointsData[i++];
            const y0 = pointsData[i++];
            const x1 = pointsData[i++];
            const y1 = pointsData[i++];
            const x2 = pointsData[i++];
            const y2 = pointsData[i++];
            x = this.getCurvePoint(x0, x1, x2, t);
            y = this.getCurvePoint(y0, y1, y2, t);
        } else if (len / 2 == 4) {
            //三次
            const x0 = pointsData[i++];
            const y0 = pointsData[i++];
            const x1 = pointsData[i++];
            const y1 = pointsData[i++];
            const x2 = pointsData[i++];
            const y2 = pointsData[i++];
            const x3 = pointsData[i++];
            const y3 = pointsData[i++];
            x = this.getCubicCurvePoint(x0, x1, x2, x3, t);
            y = this.getCubicCurvePoint(y0, y1, y2, y3, t);
        }
        return egret.Point.create(x, y);
    }
    /**
     * 通过factor参数获取二次贝塞尔曲线上的位置
     * 公式为B(t) = (1-t)^2 * P0 + 2t(1-t) * P1 + t^2 * P2 
     * @param value0 P0
     * @param value1 P1
     * @param value2 P2
     * @param factor t，从0到1的闭区间
     */
    public static getCurvePoint(value0: number, value1: number, value2: number, factor: number): number {
        const result = Math.pow((1 - factor), 2) * value0 + 2 * factor * (1 - factor) * value1 + Math.pow(factor, 2) * value2;
        return result;
    }
    /**
     * 通过factor参数获取三次贝塞尔曲线上的位置
     * 公式为B(t) = (1-t)^3 * P0 + 3t(1-t)^2 * P1 + 3t^2 * (1-t) t^2 * P2 + t^3 *P3 
     * @param value0 P0
     * @param value1 P1
     * @param value2 P2
     * @param value3 P3
     * @param factor t，从0到1的闭区间
     */
    public static getCubicCurvePoint(value0: number, value1: number, value2: number, value3: number, factor: number): number {
        const result = Math.pow((1 - factor), 3) * value0 + 3 * factor * Math.pow((1 - factor), 2) * value1 + 3 * (1 - factor) * Math.pow(factor, 2) * value2 + Math.pow(factor, 3) * value3;
        return result;
    }

}

2.游戏实现

根据Bezier曲线的绘制的点击，再帧循环改变物体的位置，就可以给出曲线移动的效果。

这里demo里的三个点分别为（100,100），（500,200），（300,800）

class BezierDemoView extends eui.Component {
    private ball: egret.Shape = new egret.Shape();//小球
    private points: egret.Point[] = [];//点集
    private pIndex: number = 0;//标记小球当前对应的点的下标
    constructor() {
        super();
        this.addEventListener(eui.UIEvent.COMPLETE, this.onUIComplete, this);
        this.skinName = "BezierDemoViewSkin";
    }
    private onUIComplete(): void {
        this.points = this.drawPoints();
        this.ball.graphics.beginFill(0xbc89f3);
        this.ball.graphics.drawCircle(0, 0, 10);
        this.ball.graphics.endFill();
        this.addChild(this.ball);
        this.addEventListener(egret.Event.ENTER_FRAME, this.onUpdate, this);
    }
    /** 绘制出点集 */
    private drawPoints(): egret.Point[] {
        let pointData: number[] = [100, 100, 500, 200, 300, 800];
        let points: egret.Point[] = BezierUtil.createBezierPoints(pointData, 60);
        let len: number = points.length;
        for (let i: number = 0; i < len; i++) {
            let point: egret.Point = points[i];
            let shp: egret.Shape = new egret.Shape();
            let gp: egret.Graphics = shp.graphics;
            gp.beginFill(0xfe0035);
            gp.drawCircle(point.x, point.y, 5);
            gp.endFill();
            this.addChild(shp);
        }
        return points;
    }
    /** 帧循环,更新小球位置 */
    private onUpdate(): void {
        let point: egret.Point = this.points[this.pIndex];
        if (point) {
            this.ball.x = point.x;
            this.ball.y = point.y;
            this.pIndex++;
        } else {
            this.removeEventListener(egret.Event.ENTER_FRAME, this.onUpdate, this);
        }
    }


}

效果