【Theorem】中国剩余定理

例：孙子算经

问题描述

今有物不知其数，三三数之余二；五五数之余三；七七数之余二。问物几何？

问题分析

答：二十三。

按现代同余理论来解：23≡2*70+3*21+2*15（mod 105）

为什么在这里要用这些余数去分别乘70,21,15呢？

这道题要先化为一个一次同余方程组：

                         

 说一下“≡”这个符号：

（1）恒等于号；（2）等价于号；（3）同余符号；（4）全等符号（相当于≌）。

而（3）中一般表示为：a≡b(mod i)

读作a同余于b模i。

 

（若X为这个方程组的解，那么X+105*k（k为整数）的解也相同，因为余数相等）

古人也有句古话（这好像有语病）：三人同行七十稀，五树梅花廿一枝，七子团圆月正半，除百零五便得知。

 这句口诀其实已经告诉了我们要先解出这三个很特殊的同余方程组（但我还是得讲）：

 

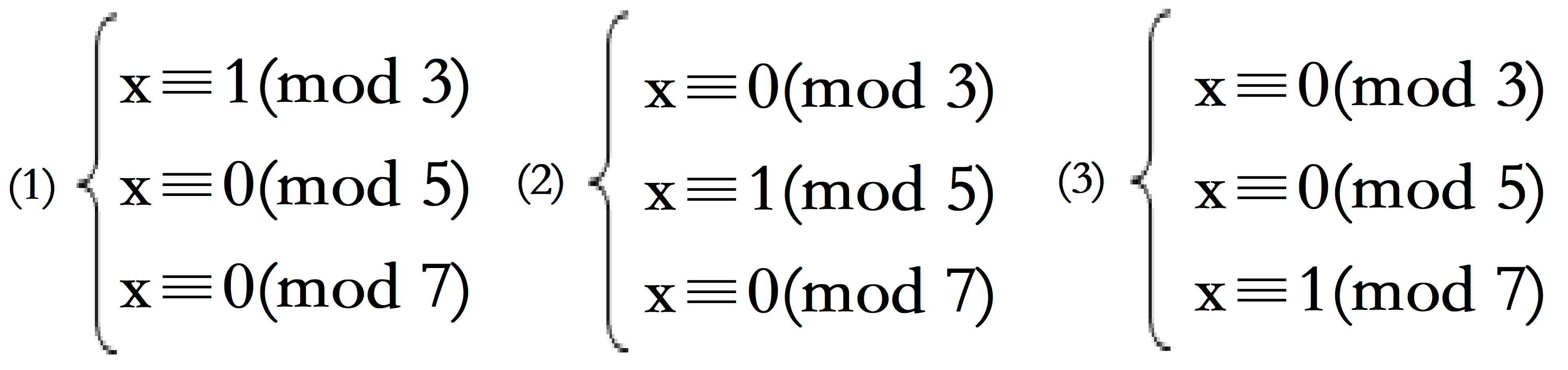
我们需要知道它们的特殊解。

在同余方程（1）中可以简化一下，相当于解这样一个同余方程：35y≡1(mod 3)。

因为我们可以看到（1）里x模5与7都是余数为0的，那么除以它们的最小公倍数是没问题的。

所以我们可以得到这里y是符合条件的数最小一个。

所以可以设想x=35y，得到变式2y≡1(mod 3),解得y≡2(mod 3).

所以x≡70(mod 105)。

 再继续按这种方法得到(2),(3)的模105的解21,15，所以有：

             

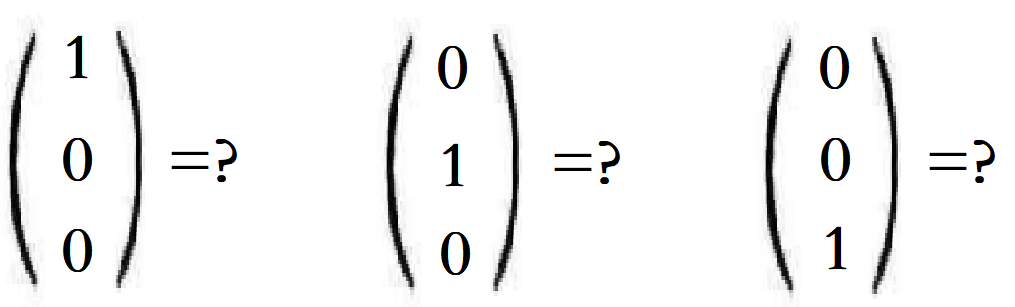
得到式子：

 

             

 

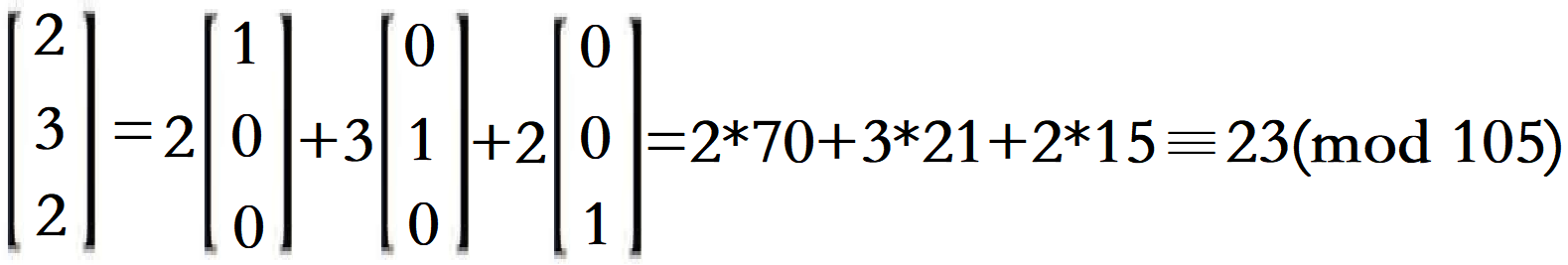
中国剩余定理（正文）

 有一组自然数m₁,m₂,m₃,...mₙ之间两两互素，且设N=m₁*m₂*m₃*...*mₙ，则得到同余方程组：

                         

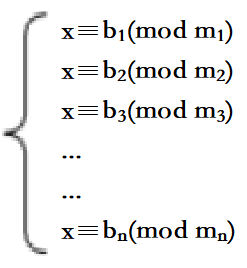
在模N同余的情况下有它的唯一解。