【转】网络流总结
推荐!!from好友的博客——【网络流】网络流小总结 http://www.cnblogs.com/KonjakJuruo/p/5560129.html
原文转载如下——(当然,我也略修改了一些东西...)
一、dinic最大流
我的模板。模板上已经有了dfs上的优化(比我以前的快多了。。)优化啊优化。

1 bool bfs(int st,int ed) 2 { 3 while(!q.empty()) q.pop(); 4 memset(d,-1,sizeof(d)); 5 q.push(st); 6 d[st]=0; 7 while(!q.empty()) 8 { 9 int x=q.front();q.pop(); 10 for(int i=first[x];i!=-1;i=a[i].next) 11 { 12 int y=a[i].y; 13 if(d[y]==-1 && a[i].d>0) 14 { 15 d[y]=d[x]+1; 16 q.push(y); 17 } 18 } 19 } 20 return (d[ed]!=-1); 21 } 22 23 int dfs(int x,int flow,int ed) 24 { 25 int k,p,r=0; 26 if(x==ed) return flow; 27 for(int i=first[x];i!=-1;i=a[i].next) 28 { 29 int y=a[i].y; 30 if(d[y]==d[x]+1 && a[i].d>0) 31 { 32 p=minn(a[i].d,flow-r); 33 p=dfs(y,p,ed); 34 r+=p; //优化,把从这个点开始能流的全部流了 35 a[i].d-=p; 36 a[i^1].d+=p; 37 } 38 if(r==flow) break; // 优化 39 } 40 if(!r) d[x]=-1; //优化 41 return r; 42 } 43 44 int dinic(int st,int ed) 45 { 46 int ans=0; 47 while(bfs(st,ed)) 48 { 49 int k; 50 while(k=dfs(st,INF,ed)) ans+=k; 51 } 52 return ans; 53 } 54 55 dinic
二、上下界网络流
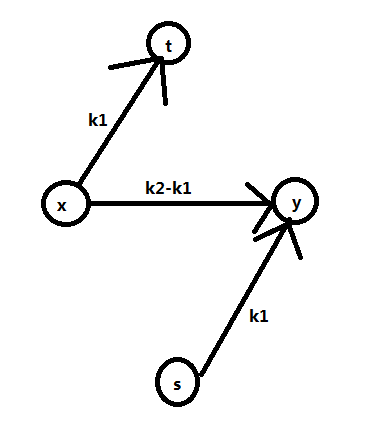
建立超级源点ss,超级汇点tt(上图中的s改为ss,t改为tt)
对于每条x到y,下界为k1,上界为k2的边(x,y,k1,k2),拆成如图这种形式:(x,y,k2-k1)(自由流),(ss,y,k1)(必须流入),(x,tt,k1)(必须流出)。
(1)没有源点和汇点:
可行流:跑一遍最大流,看是否满流。满流则有可行流。
最大流:每条边加一个费用f=1,然后跑最大费用循环流(详见下面)。
最小流:每条边加一个费用f=1,然后跑最小费用循环流。
(2)有源点和汇点:
原来的源点s,原来的汇点t。在s和t之间建边(t,s,INF),使原图变为无源汇的循环流。
可行流:拆边后跑一遍最大流,满流则有可行流。
最大流:去掉ss、tt(去掉后无论怎么跑都是已经满足了下界的可行流),然后从原来的源汇点s到t跑一遍最大流,让残余网络的增广路全部加上去。此时(s,t,INF)的那条边的反向边(t,s)的流量就是答案。
最小路:去掉ss、tt后,从原来的源汇点t到s跑一遍最大流(逆向求解,让最多的流量还回去)。
上下界网络路讲解:http://www.cnblogs.com/kane0526/archive/2013/04/05/3001108.html
模板(poj2396)

1 #include<cstdio> 2 #include<cstdlib> 3 #include<cstring> 4 #include<iostream> 5 #include<queue> 6 #include<vector> 7 using namespace std; 8 9 const int N=500,M=500,INF=(int)1e9; 10 const int S=N+M+4; 11 int n,m,s,t,ss,tt,len,sum,bk; 12 int d[N+M+4],p[N][M],first[N+M+4],map[2][N][M]; 13 struct node{int x,y,d,next;}a[N*M*2]; 14 queue<int> q; 15 16 int minn(int x,int y){return x<y ? x:y;} 17 int maxx(int x,int y){return x>y ? x:y;} 18 19 void ins(int x,int y,int d) 20 { 21 a[++len].x=x;a[len].y=y;a[len].d=d; 22 a[len].next=first[x];first[x]=len; 23 if(x==ss) sum+=d; 24 swap(x,y); 25 a[++len].x=x;a[len].y=y;a[len].d=0; 26 a[len].next=first[x];first[x]=len; 27 } 28 29 void make_edge(int x,int y) 30 { 31 if(map[0][x][y]>map[1][x][y]) bk=0; 32 if(map[0][x][y]==0) ins(x,y,map[1][x][y]); 33 else 34 { 35 ins(ss,y,map[0][x][y]); 36 ins(x,tt,map[0][x][y]); 37 ins(x,y,map[1][x][y]-map[0][x][y]); 38 } 39 } 40 41 void build(char c,int x,int y,int z) 42 { 43 int t1=0,t2=INF; 44 if(c=='=') t1=t2=z; 45 if(c=='>') t1=z+1; 46 if(c=='<') t2=z-1; 47 map[0][x][y]=maxx(map[0][x][y],t1); 48 map[1][x][y]=minn(map[1][x][y],t2); 49 50 } 51 52 bool bfs(int st,int ed) 53 { 54 while(!q.empty()) q.pop(); 55 memset(d,-1,sizeof(d)); 56 q.push(st); 57 d[st]=0; 58 while(!q.empty()) 59 { 60 int x=q.front();q.pop(); 61 for(int i=first[x];i!=-1;i=a[i].next) 62 { 63 int y=a[i].y; 64 if(d[y]==-1 && a[i].d>0) 65 { 66 d[y]=d[x]+1; 67 q.push(y); 68 } 69 } 70 } 71 return (d[ed]!=-1); 72 } 73 74 int dfs(int x,int flow,int ed) 75 { 76 int k,p,r=0; 77 if(x==ed) return flow; 78 for(int i=first[x];i!=-1;i=a[i].next) 79 { 80 int y=a[i].y; 81 if(d[y]==d[x]+1 && a[i].d>0) 82 { 83 p=minn(a[i].d,flow-r); 84 p=dfs(y,p,ed); 85 r+=p; 86 a[i].d-=p; 87 a[i^1].d+=p; 88 } 89 } 90 if(!r) d[x]=-1; 91 return r; 92 } 93 94 int dinic(int st,int ed) 95 { 96 int ans=0; 97 while(bfs(st,ed)) 98 { 99 int k; 100 while(k=dfs(st,INF,ed)) ans+=k; 101 } 102 return ans; 103 } 104 105 int main() 106 { 107 freopen("a.in","r",stdin); 108 freopen("a.out","w",stdout); 109 int T; 110 scanf("%d",&T); 111 while(T--) 112 { 113 scanf("%d%d",&n,&m); 114 int x,y,z,k; 115 char c; 116 s=n+m+1;t=s+1;ss=t+1;tt=ss+1; 117 len=-1;sum=0;bk=1; 118 memset(first,-1,sizeof(first)); 119 memset(map[0],0,sizeof(map[0])); 120 memset(map[1],63,sizeof(map[1])); 121 memset(p,0,sizeof(p)); 122 int sum1=0,sum2=0; 123 for(int i=1;i<=n;i++) 124 { 125 scanf("%d",&x); 126 map[0][s][i]=map[1][s][i]=x; 127 make_edge(s,i); 128 sum1+=x; 129 } 130 for(int i=n+1;i<=n+m;i++) 131 { 132 scanf("%d",&x); 133 map[0][i][t]=map[1][i][t]=x; 134 make_edge(i,t); 135 sum2+=x; 136 } 137 if(sum1!=sum2) bk=0; 138 scanf("%d",&k); 139 for(int i=1;i<=k;i++) 140 { 141 scanf("%d%d",&x,&y);getchar(); 142 scanf("%c%d",&c,&z); 143 if(x && y) build(c,x,y+n,z); 144 if(!x && y) 145 for(int j=1;j<=n;j++) 146 build(c,j,y+n,z); 147 if(x && !y) 148 for(int j=1;j<=m;j++) 149 build(c,x,j+n,z); 150 if(!x && !y) 151 for(int j=1;j<=n;j++) 152 for(int l=1;l<=m;l++) 153 build(c,j,l+n,z); 154 } 155 for(int i=1;i<=n;i++) 156 for(int j=n+1;j<=n+m;j++) 157 make_edge(i,j); 158 ins(t,s,INF); 159 if(!bk || dinic(ss,tt)!=sum) printf("IMPOSSIBLE\n"); 160 else 161 { 162 for(int i=0;i<len;i++) 163 { 164 x=a[i].x;y=a[i].y; 165 if(x<=n+m && y<=n+m) 166 { 167 if(!p[x][y-n]) p[x][y-n]=map[0][x][y]+a[i^1].d; 168 } 169 } 170 for(int i=1;i<=n;i++) 171 { 172 for(int j=1;j<=m;j++) 173 printf("%d ",p[i][j]); 174 printf("\n"); 175 } 176 } 177 printf("\n"); 178 } 179 return 0; 180 } 181 182 poj2396
三、最小费用最大流
在满足最大流的前提下求最小费用,就是在bfs的时候找一条费用最小的增广路。

1 void ins(int x,int y,int d,int f) 2 { 3 a[++len].x=x;a[len].y=y;a[len].d=d;a[len].f=f; 4 a[len].next=first[x];first[x]=len; 5 a[++len].x=y;a[len].y=x;a[len].d=0;a[len].f=-f; 6 a[len].next=first[y];first[y]=len; 7 } 8 9 int bfs(int st,int ed) 10 { 11 while(!q.empty()) q.pop(); 12 memset(pre,-1,sizeof(pre)); 13 memset(dis,63,sizeof(dis)); 14 memset(in,0,sizeof(in)); 15 memset(flow,0,sizeof(flow)); 16 pre[st]=0;dis[st]=0;in[st]=1;flow[st]=INF;q.push(st); 17 while(!q.empty()) 18 { 19 int x=q.front();in[x]=0;q.pop(); 20 for(int i=first[x];i!=-1;i=a[i].next) 21 { 22 int y=a[i].y; 23 if(a[i].d && dis[y]>dis[x]+a[i].f) 24 { 25 dis[y]=dis[x]+a[i].f; 26 pre[y]=i; 27 flow[y]=minn(a[i].d,flow[x]); 28 if(!in[y]) {in[y]=1;q.push(y);} 29 } 30 } 31 } 32 if(pre[ed]==-1) return -1; 33 return flow[ed]; 34 } 35 36 void MFMC(int st,int ed)//max flow min cost 37 { 38 int k,p; 39 fl=0,cl=0; 40 while((k=bfs(st,ed))!=-1) 41 { 42 fl+=k; 43 cl+=dis[ed]*k; 44 p=ed; 45 while(p!=st) 46 { 47 a[pre[p]].d-=k; 48 a[pre[p]^1].d+=k; 49 p=a[pre[p]].x; 50 } 51 } 52 } 53 54 费用流
四、最小割
根据最大流最小割原理,最大流就是最小割。主要是建图模型。
经典例题:一些资源,要不给A,要不给B,有相应的收益,问最大收益。写在我的题表里了。
Tips:把下面的图拖到网页的新标签页上就可放大看了~

我写了题解:http://www.cnblogs.com/KonjakJuruo/p/5516479.html
五、最大费用循环流
每条边有上下界k1、k2,费用f。问最大费用循环流。

对于每条边(x,y,k1,k2,f),拆成:
1.(x,y,k1,k1,f) (再按上下界拆边,即(s,y,k1,f) (x,t,k1,f)), (x到y之间一定要流k1的流量)
2.(y,x,k2-k1,-f) , (s,y,k2-k1,0) , (x,t,k2-f1,f); (x到y之间有k2-k1的自由流,先假设全部都可以得到,然后建(y,x,k2-k1,-f)就是给它反悔的机会,如果必须反悔就减回f*流量)
跑最大流,用k2的和判满流,满流则有解。
六、【重点来了】下面是代码以及题表:
代码还是见原博吧 (╯3╰) 【网络流】网络流小总结
| 题目 | 题意 | 题解 | 备注 | |
| poj2396 | Budget | 一个n*m的矩阵,给定每一行的和以及每一列的和,然后给定多个限制,即某个格子的上下界,要求一个可行的方案。 | 建n个点表示行,m个点表示列,原图源汇点s、t。 s连到表示第i行的点,上下界都为sum[i](行) 表示第i列的点连到t,上下界都为sum[i](列) 然后表示第i行的点x和表示第j行的点y中间连一条边,上下界就是约束。 错了很久,注意: 1.边数要足够大 2.p数组一开始没有清空 3.dfs的优化(不断找,用r储存已用的流量) 快超级多。 |
上下界网络流 可行流 矩阵模型 模板题 |
| LA5095 | Transportation | 一个n个点、m条边的有向图,1为起点,n为终点,要从起点运k个物体到终点,每条边的费用与流量关系:f=ax^2,问最小费用。 | 重新开一个源点,源点到1有一条流量为k、费用为0的边,然后跑最小费用最大流,如果最大流等于k则可行。 | 最小费用最大流 f=ax^i(i为自然数)模型 模板题 |
| LA3487 | Duopoly | A、B两个公司要买一些资源(他们自己买的资源不会重复),一个资源只能卖给一个公司。问最大收益。 | 方法一 把每个询问看成一个点,然后A的询问连源点,B的询问连汇点,如果AB间的某个询问有矛盾就在它们中间连一条无限大的边,ans=sum-最小割。 方法二:对于每个询问,新建一个点x,如果是A就源点连向这个点,流量为价钱p,然后连向这个询问所要求买的资源c[i],流量为INF。 如果是B则反过来,连向汇点。 |
最小割 一个费用/流量对应多个点 模板题 |
| LA5131 | Chips Challenge | 给定一个矩阵,每个格子有三种情况——不能填、能填、一定要填,要求填最多的格子,使第i行的总和等于第i列的总和,并且填的格子数不能大于总数的A/B。 | 构图:在表示第i行的点x和表示第i列的点y间连一条(y,x)的边,费用为1,然后跑最大费用流。 详见博客。 |
最大费用循环流 模板题 |
| LA2796 | Concert Hall Scheduling | 你有2个房间,有365天,有n个人找你租房,第i个人要从第xi到第yi天要一个房(任意一个),付wi的钱,求怎样安排收的钱最多 | 建365个点,连(i,i+1,2,0)的边(流量2(2个房间),费用0),源点连1,流量2费用0,365连汇点,流量2费用0。然后对于一个询问(xi,yi,wi),连(xi,yi+1,2,wi)的边,注意是yi+1,不然yi这个点可能同时作为别人的起点,然后重复就WA了。跑一遍最大费用流。 | 最大费用流 区间模型 |
| uva1515 | Pool construction | 给一个m*n的矩阵,每个格子中是#和.两个符号之一,分别代表草和洞。现在要将洞给围起来(将草和洞分离),每条边需花费b元(即将一个洞包起来需要4边,将2个连续的洞包起来需要6边,省了2条边)。有个特殊能力,能将洞变成草,花费f。当然也能将草变成洞,花费d。围起洞来需要多少花费。矩阵四周最边边的格子都必须是草,即出现洞就必须转草。 | s代表草,t代表洞; 对于每个点x,如果是草,建边(s,x,0),(x,t,d); 如果是洞,建边(s,x,f),(x,t,0) 如果一定要选,那到另一个的流量就是INF(代价无穷大) 对于每对相邻的点(x,y),建(x,y,b),(y,x,b) 这样就可以保证当x、y是不同的东西,最小割的时候就必须加上b的代价,那就是洞包起来的代价。 |
二分图模型 最小割 |
| LA2197 | Paint the Roads | n个点m条边的带权有向图,现在要将某些边涂上颜色,使得每个点恰好在k个有颜色的环上,总费用最小。 | 题意->每个点每一秒流入和流出的流量都是k->最小费用循环流 把一个点拆成两个点,这两个点之间连一条边,上下界都是k,然后跑有上下界的最小费用循环流。 对于每条边(x,y,k1,k2,f),拆成:(x,y,k1,k1,f)(再按上下界拆边,即(s,y,k1,f) (x,t,k1,f)),(y,x,k2-k1,-f),(s,y,k2-k1,0),(x,t,k2-f1,f),用k2的和判满流。 |
最小费用循环流 拆点 |
| hdu3081 | Marriage Match II | n个女生与n个男生配对,每个女生只能配对某些男生,有些女生相互是朋友,每个女生也可以跟她朋友能配对的男生配对。 每次配对,每个女生都要跟不同的男生配对且每个女生都能配到对。问最多能配对几轮。(n<=100) |
二分答案k,用并查集建边,每对可配对的男生与女生之间连一条流量为1的边,源点到每个女生连一条k的边,汇点连每个男生,流量为k。跑最大流。 WA了一中午,对拍都看不出错,然后是一个i打成了x,泪目。 |
最大流 二分 |
| uva10735 | Euler Circuit | 给定一个混合图(有有向边和无向边),然后要你求一条欧拉回路(遍历所有边后回到出发点)。 | 1.欧拉回路建图,给无向边定向。最终要是in[i]==out[i],那就先给无向边随便定向,d[i]=in[i]-out[i],若d[i]为奇数则无解(反一条边,d[i]会变化2)。 对于d[i]>0,则最多要改d[i]/2条入边,(i,t,d[i]/2) 对于d[i]<0,则最多要该(-d[i])/2条出边,(s,i,(-d[i])/2) 每条无向边最多更改一次,(x,y,1) 跑最大流,满流则有解。 2.输出欧拉回路(套圈算法)。随便从一个点开始遍历,走出一个圈,但是有一些边可能还没走,又有一个圈。做法就是起点开始遍历,dfs遍历其相邻的点,如果一个点没有相邻点了就压到栈里。倒序输出。 |
最大流 |
|
|
||||
|
|





