DS博客作业05--查找
| 这个作业属于哪个班级 | 数据结构--网络2011/2012 |
| ---- | ---- | ---- |
| 这个作业的地址 | DS博客作业05--查找 |
| 这个作业的目标 | 学习查找的相关结构 |
| 姓名 | 吴俊豪 |
0.PTA得分截图
1.本周学习总结
1.1 查找的性能指标
ASL（Average Search Length），即平均查找长度，在查找运算中，由于所费时间在关键字的比较上，所以把平均需要和待查找值比较的关键字次数成为平均查找长度。一个算法的ASL越大，说明时间性能差，反之，时间性能好，这也是显而易见的。
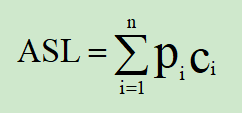
1.2 静态查找
1.2.1 顺序查找
顺序查找的基本思路是从表的一端向另一端逐个将元素的关键字和给定值k比较,若相等, 则查找成功, 给出该元素在查找表中的位置; 若整个查找表扫描结束后仍未找到关键字等于k的元素, 则查找失败.
当查找成功时,顺序查找方法查找的平均比较次数约为表长的一半:
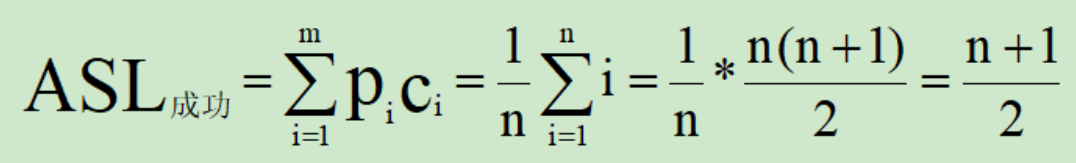
当查找不成功时,也就是扫描整个表都没有找到, 即比较了n次, 查找失败:
1.2.2 二分查找(折半查找)
二分查找的使用对象为有序表, 其查找效率相较顺序查找还是要高不少的.
当查找成功时:
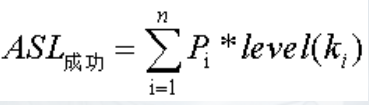
注:level为判定树的层次
当在有序数列中无法找到关键字时:
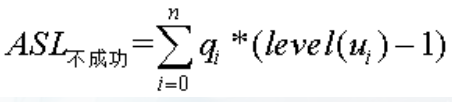
为了帮助理解,这里举一个例子:
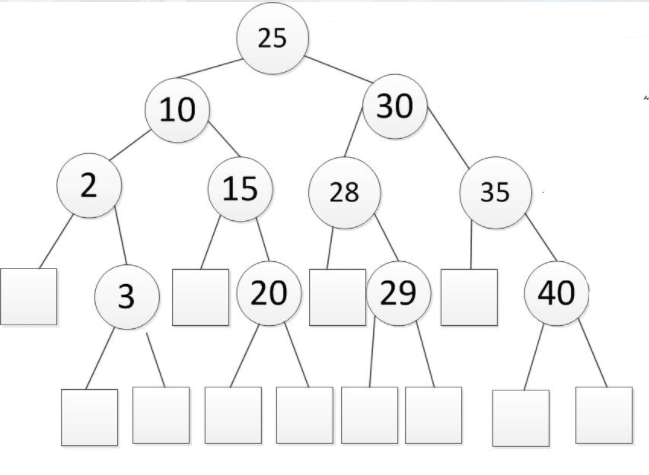
ASL(成功)=(1×1+2×2+4×3+3×4)/11=3 (这里的11为查找树的结点个数)
ASL(不成功)=(4×3+8×4)/12=3.67[3.66...] (这里12为该查找树相较完全二叉树的空节点个数)
1.3 二叉搜索树
1.3.1 如何构建二叉搜索树（操作）
构建
- 把父节点设置为根节点。
- 如果新节点内的数据值小于当前节点内的数据值，那么把当前节点设置为当前节点的左孩子。如果新节
点内的数据值大于当前节点内的数据值，那么就将当前节点设为当前节点的右孩子 - 如果当前节点的左孩子的数值为空，就把新节点插入在这里并且退出循环。否则，跳到 while 循
环的下一次循环操作中。 - 把当前节点设置为当前节点的右孩子。
- 如果当前节点的右孩子的数值为空，就把新节点插入在这里并且退出循环。否则，跳到 while 循
环的下一次循环操作中。
插入
树为空，则直接插入，返回true
树不为空，按二叉搜索树性质查找插入的位置，插入新节点
删除
节点删除的三种情况：
第一种情况：
叶子节点则直接删除
第二种情况：
若该节点，有一个节点，左或是右。因为只有一个节点，直接令祖父节点指向孙子节点，孙子节点的左右需要分开判断。
第三种情况
若该节点含有两个子节点，一般的删除策略是用其右子树的最小结点代替待删除结点的数据，然后递归删除那个右子树最小结点。即将第三种情况转化为第二种情况
1.3.2 如何构建二叉搜索树（代码）
二叉搜索树的时间复杂度是O(log2(n));
举个例子:
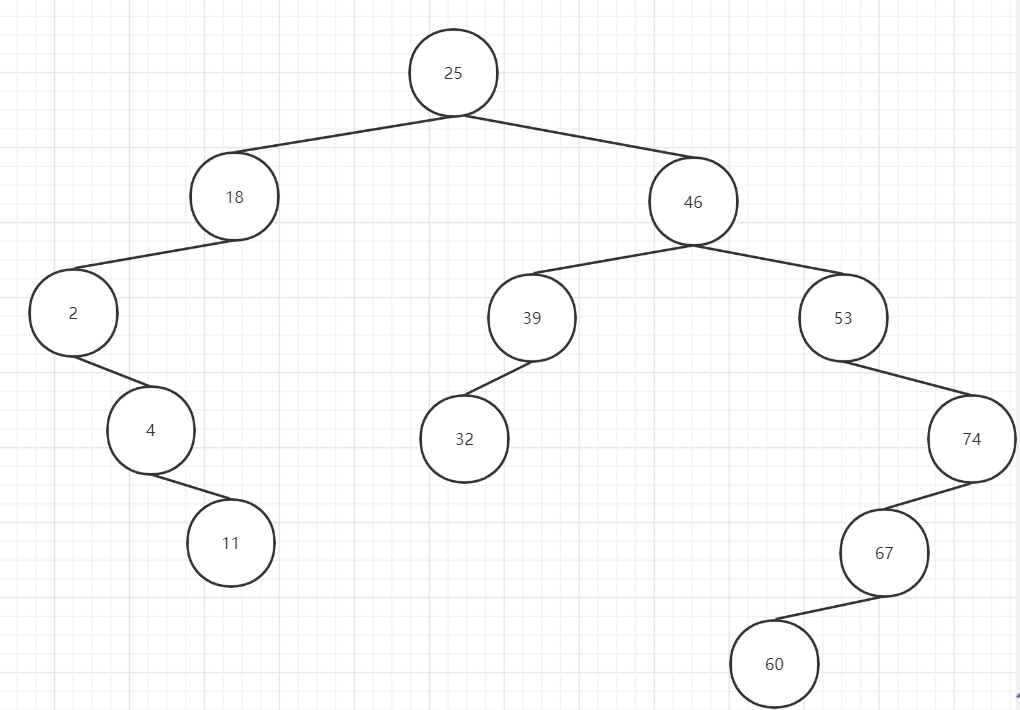
ASL成功=1×1+2×2+3×3+3×4+2×5+1×6)/12=3.5
ASL不成功=1×2+3×3+4×4+3×5+2×6)/13=4.15
二叉搜索树的构建
#include<iostream>
#include<fstream>
#include<cmath>
#include<algorithm>
using namespace std;
#define max 100
class Tree {
public:
int a[max];
int last;
};
Tree* T = new Tree; //建立一颗空的二叉搜索树
void CreateBinaryT(int p[], int left, int right, int TRoot);
int main()
{
ifstream sin("a.txt");
int n, i;
int p[max];
while (sin >> n)
{
T->last = n;
for (i = 0; i < n; i++)
sin >> p[i];
sort(p, p + n);
CreateBinaryT(p, 0, n - 1, 0);
for (i = 0; i < T->last; i++)
cout << T->a[i] << " "; //层序输出
cout << endl;
}
return 0;
}
int Getleftson(int n)//左子树结点个数
{
int l, h, i;
for (i = 0; pow(2, i) <= n; i++);
h = i - 1;;
l = n + 1 - pow(2, h);
if (l > pow(2, h - 1))
return pow(2, h) - 1;
else
return n - pow(2, h - 1);
}
void CreateBinaryT(int p[], int left, int right, int TRoot)
{
int n = right - left + 1;
if (n == 0)
return; //递归出口
int l = Getleftson(right - left + 1); //左子树节点个数
T->a[TRoot] = p[left + l];
CreateBinaryT(p, left, left + l - 1, TRoot * 2 + 1);
CreateBinaryT(p, left + l + 1, right, TRoot * 2 + 2);
}
二叉搜索树的插入:
int InsertBST(BSTree &p,KeyType k)
{
if (p==NULL)//原树为空
{
p=new BSTNode;
p->key=k;
p->lchild=p->rchild=NULL;
return 1;
}
else if (k==p->key) //相同关键字的节点0
return 0;
else if (k<p->key)
return InsertBST(p->lchild,k);//插入到左子树
else
return InsertBST(p->rchild,k);//插入到右子树
}
二叉搜索树的删除
void deleteBst(TreeNode** r, TreeNode* P)
{
TreeNode* t = *r;
TreeNode* parent = getParentBst(t, P);
TreeNode* minRight; //找到右节点为树的最小节点
if (*r == NULL || P == NULL)
return;
if (P->_left == NULL && P->_right == NULL) //第一种情况
{
if (*r == P)
{
free(t);
*r = NULL;
return;
}
if (parent->_left == P)
parent->_left = NULL;
else
parent->_right = NULL;
free(P);
return;
}
else if (P->_left != NULL && P->_right == NULL)//第二种
{
if (*r == P)
{
*r = P->_left;
free(P);
return;
}
if (parent->_left == P)
parent->_left = P->_left;
else
parent->_right = P->_left;
free(P);
return;
}
else if (P->_left == NULL && P->_right != NULL)//第二种
{
if (*r == P)
{
*r = P->_right;
free(P);
return;
}
if (parent->_left == P)
parent->_left = P->_right;
else
parent->_right = P->_right;
free(P);
return;
}
else
{
minRight = getMinBst(P->_right);
P->_data = minRight->_data;
parent = getParentBst(t, minRight);
if (minRight == P->_right)
parent->_right = minRight->_right; //这里P的_right无论是否为空都可以
else
parent->_left = minRight->_right;
free(minRight);
}
1.4 AVL树
1.4.1 AVL树解决什么问题，其特点是什么？
AVL树本质上还是一棵二叉搜索树，它的特点是:
- 本身首先是一棵二叉搜索树.
- 带有平衡条件:每个结点的左右子树的高度之差的绝对值(平衡因子)最多为1.
也就是说，AVL树，本质上是带了平衡功能的二叉查找树(二叉排序树，二叉搜索树).
1.4.2 结合一组数组，介绍AVL树的4种调整做法。
AVL树在保证自身平衡的时候需要四种调整方法,分别是RR,LL,RL,LR类型
RR:
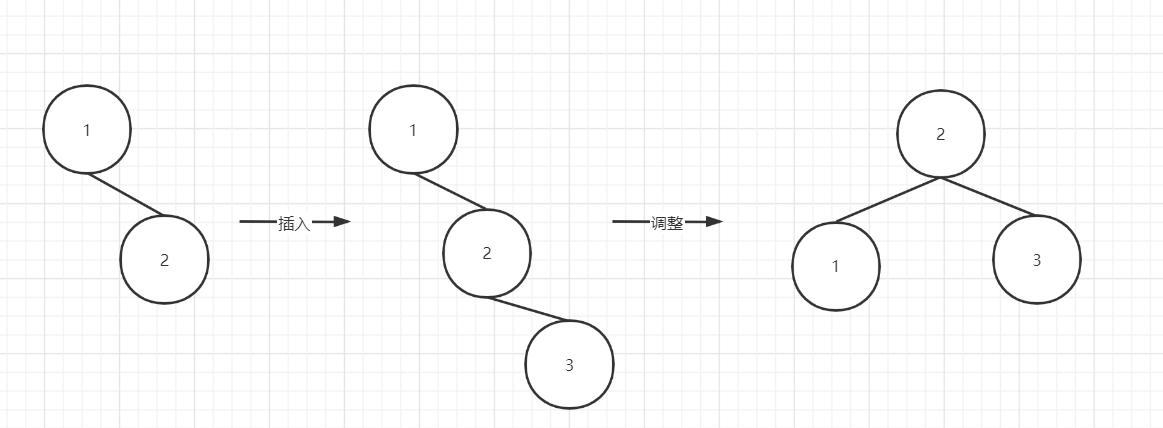
LL:
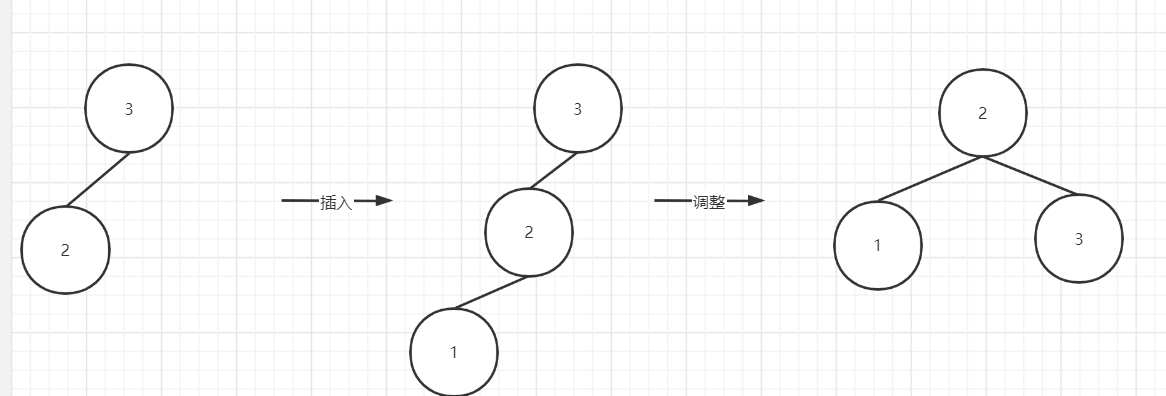
RL:
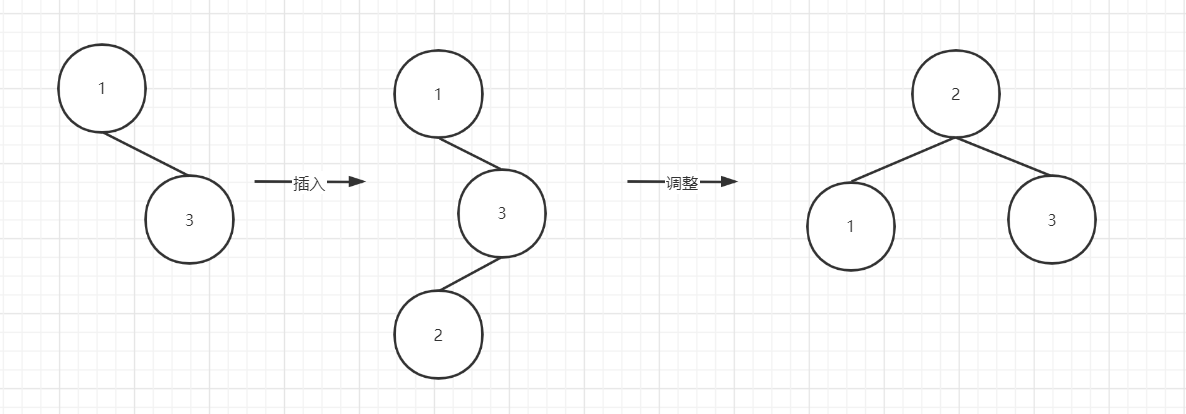
LR:
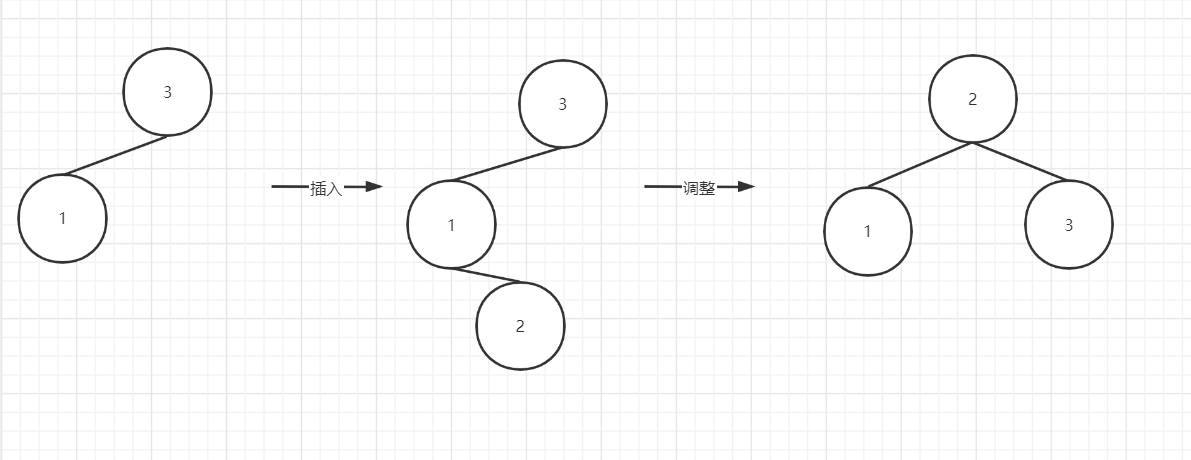
AVL树的高度和树的总节点数n的关系？
h=log2（n+1）
介绍基于AVL树结构实现的STL容器map的特点、用法。
Map是STL的一个关联容器，翻译为映射，数组也是一种映射。如：int a[10] 是int 到 int的映射，而a[5]=25,是把5映射到25。数组总是将int类型映射到其他类型。这带来一个问题，有时候希望把string映射成一个int ，数组就不方便了，这时就可以使用map。map可以将任何基本类型（包括STL容器）映射到任何基本类型（包括STL容器）。
特点：map提供关键字到值的映射 ，其中第一个可以称为关键字，每个关键字只能在map中出现一次，第二个称为该关键字的值。
用法：
begin() 返回指向map头部的迭代器
end() 返回指向map末尾的迭代器
rbegin() 返回一个指向map尾部的逆向迭代器
rend() 返回一个指向map头部的逆向迭代器
lower_bound() 返回键值>=给定元素的第一个位置
upper_bound() 返回键值>给定元素的第一个位置
empty() 如果map为空则返回true
max_size() 返回可以容纳的最大元素个数
size() 返回map中元素的个数
clear(） 删除所有元素
count() 返回指定元素出现的次数
equal_range() 返回特殊条目的迭代器对
erase() 删除一个元素
swap() 交换两个map
find() 查找一个元素
get_allocator() 返回map的配置器
insert() 插入元素
key_comp() 返回比较元素key的函数
value_comp() 返回比较元素value的函数
1.5 B-树和B+树
B-树和AVL树区别，其要解决什么问题？
索引和AVL树、B-树、B+树的关系
传统用来搜索的平衡二叉树有很多，如 AVL 树，红黑树等。这些树在一般情况下查询性能非常好，但当数据非常大的时候它们就无能为力了。原因当数据量非常大时，内存不够用，大部分数据只能存放在磁盘上，只有需要的数据才加载到内存中。一般而言，磁盘和内存的数据交互是影响系统性能的瓶颈，所以索引的效率依赖于磁盘 IO 的次数。
B-树定义。结合数据介绍B-树的插入、删除的操作，尤其是节点的合并、分裂的情况
一颗m阶的B树定义如下：
1）每个结点最多有m-1个关键字。
2）根结点最少可以只有1个关键字。
3）非根结点至少有Math.ceil(m/2)-1个关键字。
4）每个结点中的关键字都按照从小到大的顺序排列，每个关键字的左子树中的所有关键字都小于它，而右子树中的所有关键字都大于它。
5）所有叶子结点都位于同一层，或者说根结点到每个叶子结点的长度都相同。
插入操作
1）根据要插入的key的值，找到叶子结点并插入。
2）判断当前结点key的个数是否小于等于m-1，若满足则结束，否则进行第3步。
3）以结点中间的key为中心分裂成左右两部分，然后将这个中间的key插入到父结点中，这个key的左子树指向分裂后的左半部分，这个key的右子支指向分裂后的右半部分，然后将当前结点指向父结点，继续进行第3步。
删除操作
删除操作是指，根据key删除记录，如果B树中的记录中不存对应key的记录，则删除失败。
1）如果当前需要删除的key位于非叶子结点上，则用后继key（这里的后继key均指后继记录的意思）覆盖要删除的key，然后在后继key所在的子支中删除该后继key。此时后继key一定位于叶子结点上，这个过程和二叉搜索树删除结点的方式类似。删除这个记录后执行第2步
2）该结点key个数大于等于Math.ceil(m/2)-1，结束删除操作，否则执行第3步。
3）如果兄弟结点key个数大于Math.ceil(m/2)-1，则父结点中的key下移到该结点，兄弟结点中的一个key上移，删除操作结束。
否则，将父结点中的key下移与当前结点及它的兄弟结点中的key合并，形成一个新的结点。原父结点中的key的两个孩子指针就变成了一个孩子指针，指向这个新结点。然后当前结点的指针指向父结点，重复上第2步。
有些结点它可能即有左兄弟，又有右兄弟，那么我们任意选择一个兄弟结点进行操作即可。
B+树定义，其要解决问题
定义
各种资料上B+树的定义各有不同，一种定义方式是关键字个数和孩子结点个数相同。这里我们采取维基百科上所定义的方式，即关键字个数比孩子结点个数小1，这种方式是和B树基本等价的。上图就是一颗阶数为4的B+树。
除此之外B+树还有以下的要求。
1）B+树包含2种类型的结点：内部结点（也称索引结点）和叶子结点。根结点本身即可以是内部结点，也可以是叶子结点。根结点的关键字个数最少可以只有1个。
2）B+树与B树最大的不同是内部结点不保存数据，只用于索引，所有数据（或者说记录）都保存在叶子结点中。
3） m阶B+树表示了内部结点最多有m-1个关键字（或者说内部结点最多有m个子树），阶数m同时限制了叶子结点最多存储m-1个记录。
4）内部结点中的key都按照从小到大的顺序排列，对于内部结点中的一个key，左树中的所有key都小于它，右子树中的key都大于等于它。叶子结点中的记录也按照key的大小排列。
5）每个叶子结点都存有相邻叶子结点的指针，叶子结点本身依关键字的大小自小而大顺序链接。
1.6 散列查找
1.6.1 哈希表的设计主要涉及哪几个内容？
散列 (Hashing) 是一种重要的查找方法。它的基本思想是：以数据对象的关键字 key 为自变量，通过一个确定的函数关系 h，计算出对应的函数值 h(key) ，把这个值解释为数据对象的存储地址（可能不同的关键字会映射到同一个散列地址上会有冲突，需要解决），并按此存放，即“存储位置= h(key)”。
散列表（Hash Table）也称为哈希表。
散列查找的两项基本工作：
计算位置：构造散列函数确定关键字存储位置
解决冲突：应用某种策略解决多个关键词位置
从网上找来的一张用几种不同的方法解决冲突时哈希表的平均查找长度的总结图
1.6.2 结合数据介绍哈希表的构造及ASL成功、不成功的计算
题目: 以数组{18,2,10,6,78,56,45,50,110,8}为例,散列函数为：H(key)=key)mod 11, 装填因子为0.77
ASL(成功)=(1×9+2+3×2+4)/10=1.8
ASL(不成功)=(6+5+4+3+2+1+6+5+4+3+2)/11=41/11
1.6.3 结合数据介绍哈希链的构造及ASL成功、不成功的计算
题目:(25，10，8，27，32，68)，散列表的长度为8，散列函数H(k)=k mod 7
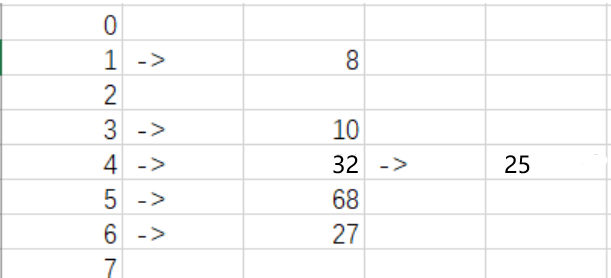
ASL(成功)=15+21)/6=7/6=1.17
ASL(不成功)=0+1+0+1+2+1+1)/7=6/7=0.86
2.PTA题目介绍
2.1 是否完全二叉搜索树
2.1.1 解题思路
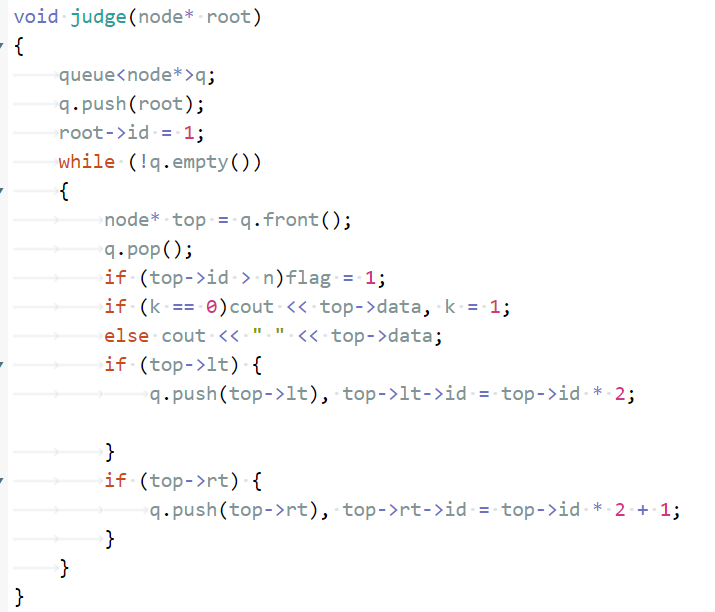
创建一个二叉树结点的结构体node, 其中包含两个左右结构体指针和数据以及每个结构体的编号(id)
再用插入的方法建立一个二叉排序树, 将建好的二叉排序树传入判断函数(judge),在判断函数中, 先将根节点入队并将根节点的id编号为1, 对二叉排序树进行层次遍历, 遍历时结合二叉排序树孩子结点的排序分别是父亲结点的2倍和2倍+1对其进行编号, 再者根据二叉排序树是完全二叉树的特性, 其每一个子节点的编号(id)肯定不会大于总结点个数n对二叉排序树进行判断,并返回判断结果
2.1.2 提交列表
2.1.3 本题知识点
二叉排序树的特性, 二叉树的层次遍历
2.2 航空公司VIP客户查询
2.2.1 解题思路
主要通过哈希表来寻找对应的人
（1）根据输入的人数，初始化一个哈希表，哈希表中包括表的长度和表的元素结点的地址数组（用于将下标匹配相应的哈希值）
（2）循环输入n个人的身份证号码和里程，进行判断，
1、先将此身份证号通过相应的算法得到哈希值
2、如果这个人是第一次记录，则创造新的结点存储信息，如果已经存在了该人，直接累加里程
3、在计算某个身份证对应的地址时，先计算相应的哈希值得到其在地址数字中的下标，当此下标对应的地址的下一个结点存在且下一个结点存储的id与当前不同时，将指针后移，这样就能防止哈希表的冲突出现
（3）根据输入的身份证号查询相关里程
2.2.2 提交列表
2.2.3 本题知识点
哈希表解决哈希冲突问题和优化算法时间
2.3 基于词频的文件相似度
2.3.1 解题思路
1、存储：用一张哈希表存储单词以及对应所在的文件，再用一张文件表，存储每个文件的词汇量以及单词在哈希表中的位置
2、查询：先在文件表中查询对应的文件名，（取文件词汇量较少的文件名）-> 找到对应文件名中的词汇所在位置-> 根据此单词的位置到哈希表中查找单词所在文件列表->从而判断该单词是否是两文件的公共词汇
2.3.2 提交列表
2.3.3 本题知识点
拉链法构造哈希表,map容器
本文来自博客园，作者：Qurare，严禁转载至CSDN平台, 其他转载请注明原文链接：https://www.cnblogs.com/konjac-wjh/p/14881913.html
